吉林大学：《高等数学》课程电子教案（PPT课件）第一章 函数、极限、连续 §2 数列的极限

第一章 §2款列的极限 数列极限的定义 二、收敛数列的性质 三、极限存在准则 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第一章 二 、收敛数列的性质 三 、极限存在准则 一、数列极限的定义 机动 目录 上页 下页 返回 结束 §2 数列的极限

一、数列极限的定义 引例.设有半径为r的圆，用其内接正n边形的面积 An逼近圆面积S 如图所示，可知 π An =nr2sin π cos- n n (n=3,4,5,…)） 当n无限增大时，An无限逼近S刘徽割圆术) 数学语言描述：VE>0,3正整数N,当n>N时，总有 |4n-S|Kε 刘徽 目 上页下页返回结束

数学语言描述: r 一 、数列极限的定义 引例. 设有半径为 r 的圆 , 逼近圆面积 S .  如图所示 , 可知 n 当 n 无限增大时, 无限逼近 S (刘徽割圆术) ,   0, 正整数N, 当 n > N 时, A − S   n 用其内接正 n 边形的面积 总有 刘徽 目录 上页 下页 返回 结束

定义：自变量取正整数的函数称为数列，记作xn=f() 或{xm}.xn称为通项（一般项） 若数列{xn}及常数a有下列关系 V6>0,正数N,当n>N时，总有xn-aN) 几何解释： 即xn∈U(a,8) a-E XN+1 XN+2 (n>N) a+s 机动目 页返回结束

定义: 自变量取正整数的函数称为数列, 记作 或 称为通项(一般项) . 若数列 及常数 a 有下列关系 : 当 n > N 时, 总有 记作 此时也称数列收敛 , 否则称数列发散 . 几何解释 : a − a + ( ) a −  x  a + n (n  N ) 即 x (a,  ) n  (n  N ) x a n n = → lim 或 x → a (n → ) n N+1 x N+2 x 则称该数列 的极限为 a , 机动 目录 上页 下页 返回 结束

123 n 例如， 234 n+1 →1(n→w) n+1 2,143 n+(-1)n-1 234 n 收敛 xn n+ →1(n>∞) n 2,4,8，…,2”,… xn=2”→∞(n→0) 1,-1,1,…,(-10+1 散 xn=(-1)+1 趋势不定 8 机动目录上页下页返回结束

例如,  , 1 , , 4 3 , 3 2 , 2 1 n + n +1 = n n xn →1 (n →) n n x n n 1 ( 1) − + − = →1 (n →) 2 , 4 , 8 ,  , 2 n ,  n n x = 2 → (n →) 1 ( 1) + = − n n x 趋势不定 收 敛 发 散 机动 目录 上页 下页 返回 结束

例1.已知x,=”+(-1”, 证明数列{xn}的极限为1， n 证：xn-1= r- n e>0,欲使xn1 n 因此，取N=],则当n>N时，就有 2-e 故 lim=lim n+(-=】 n-→o∞ n-→o0 n 机动目录上页下页返回结束

例1. 已知 证明数列 的极限为1. 证: xn −1 = 1 ( 1) − + − n n n   0 , 欲使 即 只要  1 n  因此 , 取 ], 1 [  N = 则当 n  N 时, 就有 −   + − 1 ( 1) n n n 故 1 ( 1) lim lim = + − = → → n n x n n n n 机动 目录 上页 下页 返回 结束

例2.已知xn= (-1)% 证明1imxn=0. (n+1)2 n->0 n+1)2 (n+12 n+1 Vs∈(0,1)，欲使xn-0 -1 n+1 取N=[-1],则当n>N时，就有xn-0<&, 故 lim=lim (-1)” =0 n-→o0 n-→ (n+1)2 也可由x-0= 说明：N与8有关，但不唯一. 取N=[-1] 不一定取最小的N 机动目录上页下页返回结束

例2. 已知 证明 证: xn − 0 = 2 ( 1) 1 + = n 1 1 +  n  (0,1), 欲使 只要 , 1 1   n + 即 n  取 1], 1 = [ −  N 则当 n  N 时, 就有 − 0   , n x 故 0 ( 1) ( 1) lim lim 2 = + − = → → n x n n n n 故也可取 [ ] 1  N = 也可由 2 ( 1) 1 0 + − = n n x 1. 1 −  N 与  有关, 但不唯一. 不一定取最小的 N . 说明: 取  1  1 = −  N 机动 目录 上页 下页 返回 结束

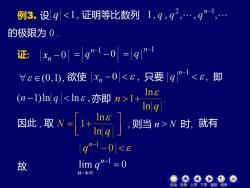
例3.设q1+ In g 因t取N[]当时 q-1-0<6 故 lim g"1 0 8 机动目录 上页下页返回结束

例3. 设 q 1, 证明等比数列 证: − 0 n x 欲使 只要 即 亦即 因此 , 取   +   = q N ln ln 1  , 则当 n > N 时, 就有 −   − 0 n 1 q 故 lim 0 1 = − → n n q . ln ln 1 q n   + 的极限为 0 . 机动 目录 上页 下页 返回 结束

二、收敛数列的性质 1.收敛数列的极限唯一 2.收敛数列一定有界. 3.收敛数列的保号性， 4.收敛数列的任一子数列收敛于同一极限 机动目录上页下页返回结束

二、收敛数列的性质 1. 收敛数列的极限唯一. 机动 目录 上页 下页 返回 结束 2. 收敛数列一定有界. 3. 收敛数列的保号性. 4. 收敛数列的任一子数列收敛于同一极限

说明： 由此性质可知，若数列有两个子数列收敛于不同的极 限，则原数列一定发散 例如 xn=(-1)+1(n=1,2,…)发散！ lim x2-1 =1; lim x2k =-1 k→00 k-→0∞ 三、极限存在准则 夹逼准则； 单调有界准则： 柯西审敛准则 机动目 上贡下页返回结束

三、极限存在准则 由此性质可知 , 若数列有两个子数列收敛于不同的极 限 , 例如， lim 2 = −1 → k k x 发散 ! 夹逼准则; 单调有界准则; 柯西审敛准则 . 则原数列一定发散 . 机动 目录 上页 下页 返回 结束 说明:

香等数兴 第代讲 感刊的极很 主讲教师：陈殿友 总课时：128

主讲教师：陈殿友 总课时：128 第七讲 数列的极限