《通信原理实验》课程电子教案（PPT讲稿）MATLAB与通信仿真（英文）Chapter 2 Analog Modulation（Frequency Modulation、Phase Modulation）

Analog Modulation Angle Modulation FM(Frequency Modulation) PM(Phase Modulation)

Analog Modulation Angle Modulation - FM(Frequency Modulation) - PM(Phase Modulation)

Angle modulation Nonlinear modulation Requires high bandwidth Good performance in the presence of noise Used in situations where BW is not a major concern and high SNR is required ■FM is used in High fidelity FM broadcasting s TV audio broadcasting Microwave carrier modulation Point-to-Point communications system

Angle modulation ◼ Nonlinear modulation ◼ Requires high bandwidth ◼ Good performance in the presence of noise ◼ Used in situations where BW is not a major concern and high SNR is required ◼ FM is used in ◼ High fidelity FM broadcasting ◼ TV audio broadcasting ◼ Microwave carrier modulation ◼ Point-to-Point communications system

Representation of PM and FM Complex envelope in angle modulated signal z(t)）=Ae Envelope is real:V(t)==(t)=4 Phase is linear function of message signal m(t) But,z(t)is nonlinear function of m(t) Angle-modulated signal ■u(t)=A.cos(2πft+0(t) Carrier is c(t)=cos(2zft) ■In text::z(t)=eo,c(t)=Acos(2πft)

Representation of PM and FM ◼ Complex envelope in angle modulated signal ◼ ◼ Envelope is real: ◼ Phase is linear function of message signal m(t) ◼ But, z(t) is nonlinear function of m(t) ◼ Angle – modulated signal ◼ ◼ Carrier is : ◼ In text: , ( ) ( ) j t c z t A e  = ( ) ( ) V t z t A = = c ( ) cos(2 ( )) u t A f t t = + c c   ( ) cos(2 ) c c t f t =  ( ) ( ) j t z t e  = ( ) cos(2 ) c c c t A f t = 

Representation of PM and FM ■PM Phase is directly proportional to m(t) ■0(t)=k,m() ■k。:deviation constants of PM Or Phase sensitivity of PM FM Phase is proportional to the integral of m(t) )=2πk,m()d k,:deviation constants of PM

Representation of PM and FM ◼ PM ◼ Phase is directly proportional to m(t) ◼ ◼ : deviation constants of PM ◼ Or Phase sensitivity of PM ◼ FM ◼ Phase is proportional to the integral of m(t) ◼ ◼ : deviation constants of PM ( ) ( ) p  t k m t = p k ( ) 2 ( ) t f     t k m d − =  f k

Relation between PM and FM Assume two message signal ·m,)for PM and m)for FM Then we have ■2πk∫'m,(r)dr=k,m,(0) aa k。dmn(t) 。m(0= 2πkdh We can generate PM from FM,and vice versa

Relation between PM and FM ◼ Assume two message signal ◼ mp (t) for PM and mf (t) for FM ◼ Then we have ◼ ◼ ◼ ◼ We can generate PM from FM, and vice versa 2 ( ) ( ) t f f p p    k m d k m t − =  2 ( ) ( ) t f p f p k m t m d k    − =  ( ) ( ) 2 p p f f k dm t m t k dt =

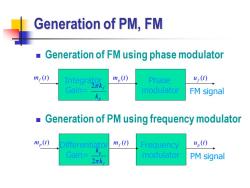
Generation of PM,FM Generation of FM using phase modulator mr(t) Integrator m (t) Phase u,(t) Gain与 modulator FM signal ■ Generation of PM using frequency modulator m,(t) Differentiator m,(t) Frequency u,(t) Gain= modulator 2nk PM signal

Generation of PM, FM ◼ Generation of FM using phase modulator ◼ Generation of PM using frequency modulator Integrator Gain= 2 f p k k  Phase modulator ( ) m t f ( ) m t p ( ) f u t FM signal Differentiator Gain= 2 p f k  k Frequency modulator ( ) m t p ( ) m t f ( ) p u t PM signal

PM and FM in Frequency domain ■Very complex Due to the nonlinearity For analysis,assume m(t)is sinusoidal ·m,()）=acos(2πfmf),m,(t)=-asin(2πfm) Then,the modulated signal u,(t)=A.cos{2πft+k,acos(2πfmt)}=Acos{2πft+B,cos(2πfmt)} 马0=cs2zu+艺co2x}=A2/+B,ea20州》

PM and FM in Frequency domain ◼ Very complex ◼ Due to the nonlinearity ◼ For analysis, assume m(t) is sinusoidal ◼ ◼ Then, the modulated signal ( ) cos(2 ), ( ) sin(2 ) m t a f t m t a f t p m f m = = −   ( ) cos{2 cos(2 )} cos{2 cos(2 )} ( ) cos{2 cos(2 )} cos{2 cos(2 )} p c c p m c c p m f f c c m c c f m m u t A f t k a f t A f t f t k a u t A f t f t A f t f t f           = + = + = + = +

Modulation index of PM and FM ■For sinusoidal m(t) ■Phase modulation index:p。=kna Peak phase deviation More phase shift for a large magnitude a k a Frequency modulation index:A,= Peak frequency deviation More phase shift for al large magnitude a and small frequency fm In general,for non-sinusoidal m(t) ■B。=k max m(t)l),p,= k,max m(t) W W is Bandwidth of m(t)

Modulation index of PM and FM ◼ For sinusoidal m(t) ◼ Phase modulation index : ◼ Peak phase deviation ◼ More phase shift for a large magnitude a ◼ Frequency modulation index: ◼ Peak frequency deviation ◼ More phase shift for al large magnitude a and small frequency fm ◼ In general, for non-sinusoidal m(t) ◼ ◼ W is Bandwidth of m(t) p p  = k a max ( ) max ( ) , f p p f k m t k m t W   = = f f m k a f  =

Spectrum with sinusoidal m(t) Modulated signal u.(t)(PM or FM) ■u.()=A.cos{2πf1+B.cos(2πfmf)} With complex envelope:()=4e)) ■Can be expressed as ·u(0）=Re{Ae2f+aca2fwl}=Rez(0)e2ar) z(t)can be represented by Fourier Series ,(t)is periodic with period7。=为 ■ z0）=Aem2=∑c,e2w 1=-00 Cn= T J

Spectrum with sinusoidal m(t) ◼ Modulated signal u* (t)(PM or FM) ◼ ◼ With complex envelope : ◼ Can be expressed as ◼ ◼ z(t) can be represented by Fourier Series ◼ z(t) is periodic with period ◼ * * ( ) cos{2 cos(2 )} u t A f t f t = + c c m    * ( ) cos(2 ) ( ) j t j f t m c c z t A e A e    = = * [2 cos(2 )] 2 * ( ) Re{ } Re{ ( ) } c m c j f t f t j f t u t A e z t e c     + = = 1 m m T f = * * cos(2 ) 2 / 2 cos(2 ) 2 / 2 ( ) m m m m m m j f t j nf t c n n T c j f t j nf t n T m z t A e c e A c e e dt T        =− − − = = =  

Spectrum with sinusoidal m(t) Bessel function of the first kind of nth order In c,replace Then 。6,=A」.ewd0]=AJ.a) Bessel function can not be evaluated in closed form Use table for evaluating ■Jn(B)=(-1)Jn(B) From u(t)=RefAe=Ref=(t)e) u(0）=Re(∑AJ,(B.)e2e2w}=∑AJ,(B.)cos(2π(f+nfm) n==o n=-00

Spectrum with sinusoidal m(t) ◼ Bessel function of the first kind of nth order ◼ In , replace ◼ Then ◼ ◼ Bessel function can not be evaluated in closed form ◼ Use table for evaluating ◼ ◼ From * / 2 cos(2 ) 2 / 2 m m m m T c j f t j nf t n T m A c e e dt T    − − =  * ( cos ) * 1 [ ] ( ) 2 j n n c c n c A e d A J         − − = =  * * ( ) ( 1) ( ) n n n J J −   = − 2 2 * * * ( ) Re{ ( ) } ( )cos(2 ( ) ) j f t j nf t c m c n c n c m n n u t A J e e A J f nf t        =− =− = = +   * [2 cos(2 )] 2 * ( ) Re{ } Re{ ( ) } c m c j f t f t j f t u t A e z t e c     + = = 2 m   f t =