《通信原理实验》课程电子教案（PPT讲稿）MATLAB与通信仿真（英文）Chapter 6 Binary Modulated Bandpass Signaling（2/3）

Digital Transmission via Carrier Modulation Carrier Amplitude Modulation Carrier Phase Modulation Quadrature Amplitude Modulation Carrier Frequency Modulation Synchronization in Communication Systems

Digital Transmission via Carrier Modulation Carrier Amplitude Modulation Carrier Phase Modulation Quadrature Amplitude Modulation Carrier Frequency Modulation Synchronization in Communication Systems

Preview We considered the transmission of digital information through baseband channels ■Chapter4and5 However,most communication channels are bandpass channel Remember "Why modulation is needed

Preview ◼ We considered the transmission of digital information through baseband channels ◼ Chapter 4 and 5 ◼ However, most communication channels are bandpass channel ◼ Remember “Why modulation is needed

Carrier Amplitude Modulation PAM signal in baseband Sm(t)）=Am8gr(t) Pulse whose shape determines the spectral characteristics of transmitted signal IG(012 Amplitude of mth waveform An=(2m-1-M)d,m=1,2,M 2d:Euclidean distance -W 0 W

Carrier Amplitude Modulation ◼ PAM signal in baseband ◼ ( ) ( ) m m T s t A g t = Pulse whose shape determines the spectral characteristics of transmitted signal -W 0 W |GT(f)|2 Amplitude of mth waveform 2d: Euclidean distance (2 1 ) , 1, 2,., A m M d m M m = − − =

Carrier Amplitude Modulation Amplitude Modulation of sinusoidal carrier Baseband Bandpass signal Signal sm(t)Cos(2πft) Sm(t) Carrier Cos(2πft) Transmitted signal waveform ■4m(t)=An8r(t)c0s(2πft),m=1,2,M Amplitude is changing according to Am

Carrier Amplitude Modulation ◼ Amplitude Modulation of sinusoidal carrier ◼ Transmitted signal waveform ◼ Baseband Signal sm(t) Carrier Cos(2fc t) Bandpass signal sm(t)Cos(2fc t) ( ) ( )cos(2 ), 1, 2,., u t A g t f t m M m m T c = =  Amplitude is changing according to Am

ASK(Amplitude Shift Keying) When pulse g-(t)is rectangular ,0≤t≤T 0, otherwise The amplitude modulated signal is called ASK Note that G(f)=F[g(t)]is sinc function Not bandlimited signal But,we defined effective Bandwidth(Null-to-Null)

ASK(Amplitude Shift Keying) ◼ When pulse gT (t) is rectangular ◼ ◼ The amplitude modulated signal is called ASK ◼ Note that GT (f)=F[gT (t)] is sinc function ◼ Not bandlimited signal ◼ But, we defined effective Bandwidth (Null-to-Null) 2 , 0 ( ) 0, T t T g t T otherwise     =   

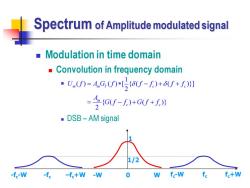
Spectrum of Amplitude modulated signal Modulation in time domain Convolution in frequency domain ·U)=A.G,()*5f-f)+f+f)川 -=GU-f0+6U+f》 DSB-AM signal 1/2 -fc-W -fc -fc+W -W W f-W f+W

Spectrum of Amplitude modulated signal ◼ Modulation in time domain ◼ Convolution in frequency domain ◼ ◼ DSB – AM signal 1 ( ) ( ) [ { ( ) ( )}] 2 { ( ) ( )} 2 m m T c c m c c U f A G f f f f f A G f f G f f =  − + +   = − + + -W 0 W 1 1/2 -fc-W -fc –fc+W fc-W fc fc+W

Constellation of Amplitude modulated signal Bandpass PAM signal can be represented w(t)=gr(t)cos(2zft) Sm=Am:m=1,2,.,M One dimensional signal with multiamplitude -3d -d d 3d Euclidean distance 2d

Constellation of Amplitude modulated signal ◼ Bandpass PAM signal can be represented ◼ ◼ One dimensional signal with multiamplitude ( ) ( ) u t s t m m =  ( ) ( )cos(2 ) T c   t g t f t = , 1, 2,., m m s A m M = = -3d -d d 3d Euclidean distance = 2d

ASK with normalized energy To be a Normalized Signal waveform ■r2o)dh=1 0 because f>>W Then gr(t)is constant Within a cycle of [yr2(0di=∫g20cos(2πf0d cos4元ft d+cos(4d=1 g(t)must be scaled to satisfies g0h=1

ASK with normalized energy ◼ To be a Normalized Signal waveform ◼ ◼ Then ◼ gT (t) must be scaled to satisfies ◼ 2  ( ) 1 t dt  − =  2 2 2 2 2 ( ) ( ) cos (2 ) 1 1 ( ) ( ) cos(4 ) 1 2 2 T c T T c t dt g t f t dt g t dt g t f t dt      − −   − − = = + =     0 because fc>>W gT(t) is constant Within a cycle of cos4fc t 1 2 ( ) 1 2 g t dt T  − = 

Demodulation of PAM signals Received signal through AWGN channel ■r(t)=Amg(t)cos(2πft)+(t) =Am8r(t)cos(2πft)+n.(t)cos(2πft)-n,(t)sin(2πft) In phase component of noise Quadrature component of noise A single correlator(or Matched filter) Since One dimensional signal Mixer to down conversion To Baseband

Demodulation of PAM signals ◼ Received signal through AWGN channel ◼ ◼ A single correlator (or Matched filter) ◼ Since One dimensional signal ◼ Mixer to down conversion ◼ To Baseband ( ) ( ) cos(2 ) ( ) ( ) cos(2 ) ( ) cos(2 ) ( ) sin(2 ) m T c m T c c c s c r t A g t f t n t A g t f t n t f t n t f t     = + = + − In phase component of noise Quadrature component of noise

Demodulation of PAM signals ■Coherent Receiver r(t)=Agr(t)cos(2nft)+n(t) 心r0w0h=J4g0cos'(2πf0h +n0)g(0cos2πf10d r(t)w(t)=A.8(t)cos2(2zft) =Am+n +n(t)g(t)cos(2nft) Received Signal Sampler w(t)=8(t)cos(2πft) 8r(1) Signal Pulse Clock cos(2πft) Generator Osc

Demodulation of PAM signals ◼ Coherent Receiver 0 ( ) t d  Osc. Signal Pulse Generator Sampler Clock Received Signal ( ) ( )cos(2 ) ( ) m T c r t A g t f t n t = +  cos(2 ) c  f t ( ) g t T ( ) ( )cos(2 ) T c   t g t f t = 2 2 ( ) ( ) ( ) cos (2 ) ( ) ( ) cos(2 ) m T c T c r t t A g t f t n t g t f t    = + 2 2 0 0 0 ( ) ( ) ( ) cos (2 ) ( ) ( ) cos(2 ) T T m T c T T c m r t t dt A g t f t dt n t g t f t dt A n    = + = +   