《通信原理实验》课程电子教案（PPT讲稿）MATLAB与通信仿真（英文）Chapter 4 Baseband Digital Transmission（Binary Signal Transmission）

Baseband Digital Transmission Binary Signal Transmission Multiamplitude Signal Transmission Multidimensional Signals

Baseband Digital Transmission Binary Signal Transmission Multiamplitude Signal Transmission Multidimensional Signals

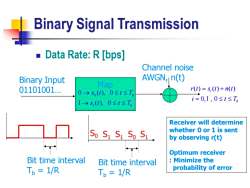
Binary Signal Transmission Data Rate:R [bps] Channel noise Binary Input AWGN,n(t) Map 01101001. r(t)=S,(t)+n(t) 0→S(t),0≤t≤T i=0,1,0≤t≤T6 1→S(),0≤t≤T Receiver will determine So S1S1 So S1 whether 0 or 1 is sent by observing r(t) Optimum receiver Bit time interval Bit time interval Minimize the To 1/R To 1/R probability of error

Binary Signal Transmission ◼ Data Rate: R [bps] Binary Input 01101001. Map 0 1 0 ( ), 0 1 ( ), 0 b b s t t T s t t T →   →   Channel noise AWGN, n(t) ( ) ( ) ( ) 0,1 , 0 i b r t s t n t i t T = + =   Bit time interval Tb = 1/R Bit time interval Tb = 1/R S0 S1 S1 S0 S1 Receiver will determine whether 0 or 1 is sent by observing r(t) Optimum receiver : Minimize the probability of error

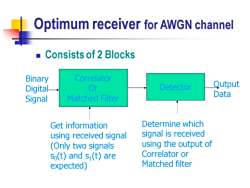
Optimum receiver for AWGN channel ■ Consists of 2 Blocks Binary Correlator Digital. Or Detector Qutput Signal Matched Filter Data Get information Determine which using received signal signal is received (Only two signals using the output of so(t)and si(t)are Correlator or expected) Matched filter

Optimum receiver for AWGN channel ◼ Consists of 2 Blocks Correlator Or Matched Filter Detector Binary Digital Signal Output Data Get information using received signal (Only two signals s0 (t) and s1 (t) are expected) Determine which signal is received using the output of Correlator or Matched filter

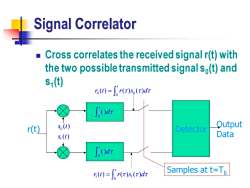
Signal Correlator ■ Cross correlates the received signal r(t)with the two possible transmitted signal so(t)and s1() (=r()s,()dr [dr r(t) 5(t) Output Detector s(t) Data i0=∫r(r)s(r)d Samples at t=Tp

Signal Correlator ◼ Cross correlates the received signal r(t) with the two possible transmitted signal s0 (t) and s1 (t) 0 ( ) t d  0 ( ) t d  r(t) Detector 0 1 ( ) ( ) s t s t Output Data 0 0 0 ( ) ( ) ( ) t r t r s d =     1 1 0 ( ) ( ) ( ) t r t r s d =     Samples at t=Tb

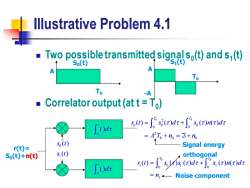
Illustrative Problem 4.1 Two possible transmitted signalso(t)and s(t) So(t) s,(t) A Tb -A Correlator output(at t=To) ((dr+"s(n(r)dr =AT,+n=5+n r(t)= 50(t) Signal energy So(t)+n(t) S,() orthogonal Odr ((d((dr =n←-Noise component

Illustrative Problem 4.1 ◼ Two possible transmitted signal s0 (t) and s1 (t) ◼ Correlator output (at t = T0 ) A Tb A Tb S0(t) S1(t) -A 0 ( ) t d  0 ( ) t d  r(t)= S0(t)+n(t) 0 1 ( ) ( ) s t s t 2 0 0 0 0 0 2 0 0 ( ) ( ) ( ) ( ) T T b b b r t s d s n d A T n n = +      = + =  +   1 0 1 1 0 0 1 ( ) ( ) ( ) ( ) ( ) T T b b r t s s d s n d n = +       =   orthogonal Signal energy Noise component

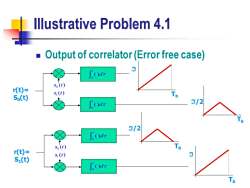
Illustrative Problem 4.1 Output of correlator(Error free case) dr So(t) r(t)= S,(t) So(t) Od: 3/2 3/2 Odr r(t)= s (t) S1(t) Odr

Illustrative Problem 4.1 ◼ Output of correlator (Error free case) 0 ( ) t d  0 ( ) t d  r(t)= S0(t) 0 1 ( ) ( ) s t s t Tb  Tb /2 0 ( ) t d  0 ( ) t d  r(t)= S1(t) 0 1 ( ) ( ) s t s t Tb  Tb /2

Illustrative Problem 4.1 ■Noise components AWGN:E[n()]=0,E[n(t)"n(t)]= No 2 no,n are Gaussian process With zero mean n]=E可s,(r)m(r)dr=∫s,(e)Lrdr]=0 En]=E可s()nr)dr]=∫s(r)Erdr]=0 ■And variances o=En]=E可∫s)s(r)n0n(r)dida]=∫∫s()s,(a)E[nu)n(didr =六50x(e-h-0h=3i=l2

Illustrative Problem 4.1 ◼ Noise components ◼ AWGN: ◼ n0 , n1 are Gaussian process ◼ With zero mean ◼ And variances 0 [ ( )] 0, [ ( ) ( )] 2 T N E n t E n t n t = = 0 0 0 0 0 1 1 1 0 0 [ ] [ ( ) ( ) ] ( ) [ ( )] ] 0 [ ] [ ( ) ( ) ] ( ) [ ( )] ] 0 b b b b T T T T E n E s n d s E n d E n E s n d s E n d             = = = = = =     2 2 0 0 0 0 0 0 0 2 0 0 [ ] [ ( ) ( ) ( ) ( ) ] ( ) ( ) [ ( ) ( )] ( ) ( ) ( ) ( ) , 1, 2 2 2 2 b b b b b b T T T T i i i i i i T T i i i E n E s t s n t n dtd s t s E n t n dtd N N N s t s t dt s t dt i           = = =  = − = = =      

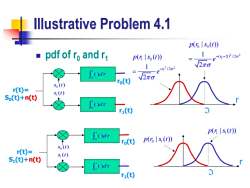
lllustrative Problem 4.1 p(r lso(t)) pdf of ro and r p(n lso(t)) e(6-d/2o e1212o2 2πo ro(t) V2π 5o(I) r(t)= S,(t) So(t)+n(t) Od: r1() Odr p(s(t)) ro(t) p(rls(t)) So(t) r(t)= S1(t)+n(t) Odr ri(t) 3

Illustrative Problem 4.1 ◼ pdf of r0 and r1 2 2 0 0 0 ( ) / 2 ( | ( )) 1 2 r p r s t e    − − = 0 ( ) t d  0 ( ) t d  r(t)= S0(t)+n(t) 0 1 ( ) ( ) s t s t r  2 2 1 1 0 / 2 ( | ( )) 1 2 r p r s t e    − = 0 ( ) t d  0 ( ) t d  r(t)= S1(t)+n(t) 0 1 ( ) ( ) s t s t r  0 1 p r s t ( | ( )) 1 1 p r s t ( | ( )) r0(t) r1(t) r0(t) r1(t)

The detector o I Decides the transmitted signal is so(t)or s(t) by observing the output of correlator(ro or r) ■Optimum detector Detector that has minimum probability of error

The detector ◼ Decides the transmitted signal is s0 (t) or s1 (t) by observing the output of correlator (r0 or r1 ) ◼ Optimum detector ◼ Detector that has minimum probability of error

Illustrative Problem 4.3 Optimal Detector ▣0ifro>r1 r ■1ifro<r1 To <r1 ■Probability of error If so(t)is transmitted,but it detect s(t) p(|s(t)) p(rls(t)) 了 Error Probability of error

Illustrative Problem 4.3 ◼ Optimal Detector ◼ 0 if r0 > r1 ◼ 1 if r0 r1 r0 < r1 r0 r1 0 1 r  0 0 p r s t ( | ( )) 1 0 p r s t ( | ( ))Error Probability of error