《通信原理实验》课程电子教案（PPT讲稿）MATLAB与通信仿真（英文）Chapter 4 Baseband Digital Transmission（Multiamplitude Signal Transmission）

Baseband Digital Transmission Multiamplitude Signal Transmission

Baseband Digital Transmission Multiamplitude Signal Transmission

Binary Vs.Multiamplitude signal Binary signal 1 bit of information Two level to represent 0 and 1 If we use multiple amplitude levels We can transmit multiple bits per signal waveform ■Question Probability of Error Vs.Bandwidth ??

Binary Vs. Multiamplitude signal ◼ Binary signal ◼ 1 bit of information ◼ Two level to represent 0 and 1 ◼ If we use multiple amplitude levels ◼ We can transmit multiple bits per signal waveform ◼ Question ◼ Probability of Error Vs. Bandwidth ???

Signal waveform with 4 amplitude levels Normalized pulse whose energy is 1 80=序0ss7 0 ,otherwise Consider 4 equally spaced Amplitude ■Am=(2m-3)d,m=0,1,2,3 ■0rAn={-3d,-d,d,3d0 4 waveform called PAM(Pulse Amplitude Modulated) signal ■Snm(t)=Ang(t),0≤t≤T See figure 4.19,page 190

Signal waveform with 4 amplitude levels ◼ Normalized pulse whose energy is 1 ◼ ◼ Consider 4 equally spaced Amplitude ◼ ◼ Or ◼ 4 waveform called PAM(Pulse Amplitude Modulated) signal ◼ ◼ See figure 4.19, page 190 1 , 0 ( ) 0 , t T g t T otherwise     =   A m d m m = − = (2 3) , 0,1, 2,3 { 3 , , ,3 } A d d d d m = − − s t A g t t T m m ( ) ( ), 0 =  

Signal waveform with 4 amplitude levels Can transmit 2 bits of information per waveform Assign information to waveform ■00→s0) ■01→s ·10→s2() .11→S3() ■ Definition of Symbol Each pair of information bits (00,01,10,11}is called symbol Time duration T is called Symbol Duration If Bit rate R=1/Tp,then Symbol interval T=2Tp

Signal waveform with 4 amplitude levels ◼ Can transmit 2 bits of information per waveform ◼ Assign information to waveform ◼ 00 → s0 (t) ◼ 01 → s1 (t) ◼ 10 → s2 (t) ◼ 11 → s3 (t) ◼ Definition of Symbol ◼ Each pair of information bits {00, 01, 10, 11} is called symbol ◼ Time duration T is called Symbol Duration ◼ If Bit rate R =1/Tb , then Symbol interval T = 2Tb

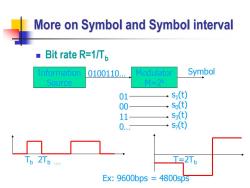
More on Symbol and Symbol interval Bit rate R=1/Tp Information 0100110 Modulator Symbol Source M=2水 01 S1(t) 00 so(t) 1 S() 0 s(t) Tp 2Tb. T=2Tb Ex:9600bps 4800sps

More on Symbol and Symbol interval ◼ Bit rate R=1/Tb Information Source 0100110. Modulator M=2k Symbol 01 00 11 0. s1 (t) s0 (t) s3 (t) s? (t) Tb 2Tb . T=2Tb Ex: 9600bps = 4800sps

Signal waveform with 4 amplitude levels Signal Constellation Diagram One dimensional signal ■g()is basis Can you imagine the effect of AWGN ? 00 01 10 11 -3d -d d 3d Euclidean distance =2d

Signal waveform with 4 amplitude levels ◼ Signal Constellation Diagram ◼ One dimensional signal ◼ g(t) is basis ◼ Can you imagine the effect of AWGN ?? -3d -d d 3d 00 01 10 11 Euclidean distance = 2d

Received Signal ■ AWGN channel assumption ■r(t)=S,(t)+n(t),m=0,1,2,3,0≤t≤T White Gaussian process With power spectrum No/2 Receiver determines which of 4 signal waveform was transmitted by observing the received signal r(t) Optimum receiver minimizes the probability of error

Received Signal ◼ AWGN channel assumption ◼ ◼ Receiver determines which of 4 signal waveform was transmitted by observing the received signal r(t) ◼ Optimum receiver minimizes the probability of error ( ) ( ) ( ), 0,1, 2,3, 0 i r t s t n t m t T = + =   White Gaussian process With power spectrum N0 /2

Optimum receiver for AWGN channel Implementation r() Correlator Amplitude Decision (Matched filter Detector Output ▣Correlator Samples at t=T r(t) -frgcoa =4g0）+n0)g0)adh g() =∫Ag'(0di+∫g0n)d =A+n

Optimum receiver for AWGN channel ◼ Implementation ◼ Correlator Correlator (Matched filter) Amplitude Detector r(t) Decision Output 0 ( ) t d  r(t) g(t) Samples at t=T 0 0 2 0 0 ( ) ( ) { ( ) ( )} ( ) ( ) ( ) ( ) T T i T T i i r r t g t dt A g t n t g t dt A g t dt g t n t dt A n = = + = + = +    

Optimum receiver for AWGN channel pdf of correlator output ■Noise component .Zero mean::ELnl=E可g)n)dh]=∫g0E]h=0 .Variance:(d No P(r|s,(t)= d.d.3d -3d -d d 3d

Optimum receiver for AWGN channel ◼ pdf of correlator output ◼ Noise component ◼ Zero mean: ◼ Variance: 0 0 [ ] [ ( ) ( ) ] ( ) [ ( )] 0 T T E n E g t n t dt g t E n t dt = = =   2 2 2 0 0 0 [ ] ( ) 2 2 N N T  = = = E n g t dt  -3d -d d 3d 2 2 1 ( ) / 2 ( | ( )) , 3 , , ,3 2 i r A P r s t e A d d d d i i    − − = = − −

Optimum Detector ■ Select the amplitude corresponding to the smallest distance ■D=r-A2i=0,1,2,3 -3d-2d -d0 d/2d 3d Average Probability of Symbol Error 8小-Ea-aE-c

Optimum Detector ◼ Select the amplitude corresponding to the smallest distance ◼ D r A i i i = − = , 0,1,2,3 -3d -2d -d d 3d 0 2d Average Probability of Symbol Error 2 2 2 / 2 4 2 / 0 3 3 1 3 3 2 ( ) ( ) ( ) 4 2 2 2 2 x m d d d P P r A d e dx Q Q    N  − = −  = = = 