《通信原理实验》课程电子教案（PPT讲稿）MATLAB与通信仿真电子教案_matlab在通信中的应用（PSK频带传输系统）

AT工AB教字领带传输素统 本节预览 >数字频带传输系统概述 >2ASK,2FSK信号的波形仿真 >4PSK的误码率的蒙特卡罗仿真 数字频带传输系统 目的：实际的信道大多都具有带通特性，所以要将基 带信号调制到高频 作用：1.**水*水*水六水六六水*六**水***六**水***水***水 2.****0*********光**0*****☆**0*六*☆**水 3.水*****必******0*******0*六六******* 2ASK 单极性不归零的信号的表达式为：s()=∑agt-nT,) 2ASK信号的表达式为：S24Sx(t)=s(t)coswt 调制系统框围为：s() →S24SK(t) cos(wt)

MATLAB 数字频带传输系统 本节预览 ➢ 数字频带传输系统概述 ➢ 2ASK,2FSK 信号的波形仿真 ➢ 4PSK 的误码率的蒙特卡罗仿真 数字频带传输系统 目的：实际的信道大多都具有带通特性，所以要将基 带信号调制到高频 作用：1.*************************************** 2.************************************** 3.************************************** 2ASK 单极性不归零的信号的表达式为： ( ) ( ) n s n s t a g t nT = −  2ASK 信号的表达式为： 2 ( ) ( )cos ASK c S t s t w t = 调制系统框图为： s t( )  cos( ) w t c 2 ( ) ASK S t

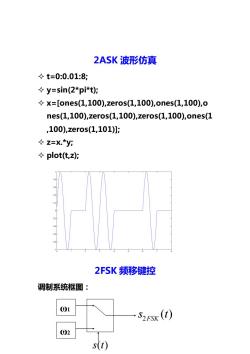
2ASK波形仿真 ◇t=0:0.01:8: ◇y=sin(2*pi*t): ◇x=[ones(1,100),zeros(1,100),ones(1,100),o nes(1,100),zeros(1,100),zeros(1,100),ones(1 ,100),zeros(1,101)]: ◇z=x.*yi ◇plot(t,z: 02 2FSK频移键控 调制系统框图： 01 -S2FSK(1) 02 s(t)

2ASK 波形仿真  t=0:0.01:8;  y=sin(2*pi*t);  x=[ones(1,100),zeros(1,100),ones(1,100),o nes(1,100),zeros(1,100),zeros(1,100),ones(1 ,100),zeros(1,101)];  z=x.*y;  plot(t,z); 2FSK 频移键控 调制系统框图： ω1 ω2 s t( ) 2 ( ) FSK s t

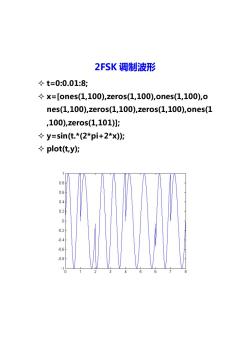
2FSK调制波形 ◇t=0:0.01:8; ◇x=[ones(1,100),zeros(1,100),ones(1,100),o nes(1,100),zeros(1,100),zeros(1,100),ones(1 ,100),zeros(1,101)]: y=sin(t.*(2*pi+2*x)); ◆plot(ty)i 0.8 0.6 4 0.2 0 0.2 0.4 0.6

2FSK 调制波形  t=0:0.01:8;  x=[ones(1,100),zeros(1,100),ones(1,100),o nes(1,100),zeros(1,100),zeros(1,100),ones(1 ,100),zeros(1,101)];  y=sin(t.*(2*pi+2*x));  plot(t,y);

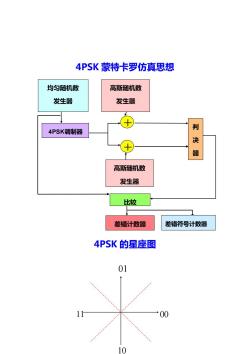
4PSK蒙特卡罗仿真思想 均匀随机数 高斯随机数 发生器 发生器 4PSK调制器 判 决 高斯随机数 发生器 比较 差错计数器 差错符号计数器 4PSK的星座图 01 00 w 10

4PSK 蒙特卡罗仿真思想 4PSK 的星座图 均匀随机数 发生器 4PSK调制器 高斯随机数 发生器 判 决 器 高斯随机数 发生器 比较 差错计数器 + + 差错符号计数器 11 00 1001

计算噪声 function[gsrv1,gsrv2]=gngauss(m,sg ma) ◇if nargin==0 m=0: sgma=1; ◇elseif nargin==l sgma=m; m=0: ◇end ◇u=rand; 令z=sgma*(sqrt(2*log(1/(1-u))； ◇u=rand; gsrv1=m+z*cos(2*pi*u); *gsrv2=m+z*sin(2*pi*u); 4PSK的蒙特卡罗仿真 目的：仿真实际误码率 function [pb,ps]=cm_sm32(snr_in_dB) N=10000: E=1: snr=10(snr_in_dB/10):

计算噪声 function[gsrv1,gsrv2]=gngauss(m,sg ma) if nargin==0 m=0; sgma=1; elseif nargin==1 sgma=m; m=0; end u=rand; z=sgma*(sqrt(2*log(1/(1-u)))); u=rand; gsrv1=m+z*cos(2*pi*u); gsrv2=m+z*sin(2*pi*u); 4PSK 的蒙特卡罗仿真 目的：仿真实际误码率 function [pb,ps]=cm_sm32(snr_in_dB) N=10000; E=1; snr=10^(snr_in_dB/10);

sgma=sgrt(E/snr)/2: s00=[10]: s01=[0,1]: s11=[-10]: 810=[0-1]: for i=1:N temp=rand; if (temp<0.25) dsourcel(i)=0: dsource2(i)=0; elseif (temp<0.5) dsourcel(i)=0: dsource2(i)=1: elseif (temp<0.75) dsourcel(i)=1; dsource2(i)=0: else dsourcel(i)=1; dsource2(i)=1: end end numofsymbolerror=0; numofbiterror=0; for i=1:N n(1)=gngauss(sgma); n(2)=gngauss(sgma); if((dsourcel(i)==0)&(dsource2(i)==0)) r=s00+n: elseif((dsourcel(i)==0)&(dsource2(i)==1)) r=s01+n: elseif((dsourcel(i)==1)&(dsource2(i)==0)) r=g10+n; else r=s11+n;

sgma=sqrt(E/snr)/2; s00=[1 0]; s01=[0,1]; s11=[-1 0]; s10=[0 -1]; for i=1:N temp=rand; if (temp<0.25) dsource1(i)=0; dsource2(i)=0; elseif (temp<0.5) dsource1(i)=0; dsource2(i)=1; elseif (temp<0.75) dsource1(i)=1; dsource2(i)=0; else dsource1(i)=1; dsource2(i)=1; end end numofsymbolerror=0; numofbiterror=0; for i=1:N n(1)=gngauss(sgma); n(2)=gngauss(sgma); if((dsource1(i)==0)&(dsource2(i)==0)) r=s00+n; elseif((dsource1(i)==0)&(dsource2(i)==1)) r=s01+n; elseif((dsource1(i)==1)&(dsource2(i)==0)) r=s10+n; else r=s11+n;

end c00=dot(r,s00计算互相关量度 c0l=dot(r,s01); c10=dot(r,s10): c11=dot(r,s11): c_cmax=max([c00 c0l cl0 cl1]): if(c00==c_cmax) decisl=0; decis2=0; elseif(c0l==c_cmax) decisl=0; decis2=1: elseif(cl0==c_cmax) decisl=1; decis2=0: else decisl=1; decis2=1; end symbolerror=0; if(decisl~=dsourcel(i)) numofbiterror=numofbiterror+l; symbolerror=1; end if(decis2~=dsource2(i)) numofbiterror=numofbiterror+l: symbolerror=l; end if(symbolerror==1) numofsymbolerror=numofsymbolerror+l; end end ps=numofsymbolerror/N: pb=numofbiterror/(2*N);

end c00=dot(r,s00);%计算互相关量度 c01=dot(r,s01); c10=dot(r,s10); c11=dot(r,s11); c_cmax=max([c00 c01 c10 c11]); if(c00==c_cmax) decis1=0; decis2=0; elseif(c01==c_cmax) decis1=0; decis2=1; elseif(c10==c_cmax) decis1=1; decis2=0; else decis1=1; decis2=1; end symbolerror=0; if(decis1~=dsource1(i)) numofbiterror=numofbiterror+1; symbolerror=1; end if(decis2~=dsource2(i)) numofbiterror=numofbiterror+1; symbolerror=1; end if(symbolerror==1) numofsymbolerror=numofsymbolerror+1; end end ps=numofsymbolerror/N; pb=numofbiterror/(2*N);

10 10 dot函数：计算两个向量之间的点积 a=[123;b=[456]; c dot(a,b) c= 3) 4PSK的理论误码率 N rerear 绘制误码率曲线 SNRindB1=0:2:10; SNRindB2=0:0.1:10: for i=1:length(SNRindB1) [pb,ps]=cm_sm32(SNRindB1(i)); smld _bit_err_prb(i)=pb; smld_symbol_err_prb(i)=ps; end for i=1:length(SNRindB2) SNR=exp(SNRindB2(i)*log(10)/10); theo_err_prb(i)=Qfunct(sqrt(2*SNR)); end

0 2 b e E P Q N   =       4PSK 的理论误码率 function [y]=Qfunct(x) y=(1/2)*erfc(x/sqrt(2)); 绘制误码率曲线 SNRindB1=0:2:10; SNRindB2=0:0.1:10; for i=1:length(SNRindB1) [pb,ps]=cm_sm32(SNRindB1(i)); smld_bit_err_prb(i)=pb; smld_symbol_err_prb(i)=ps; end for i=1:length(SNRindB2) SNR=exp(SNRindB2(i)*log(10)/10); theo_err_prb(i)=Qfunct(sqrt(2*SNR)); end dot 函数：计算两个向量之间的点积 a = [1 2 3]; b = [4 5 6]; c = dot(a,b) c = 32

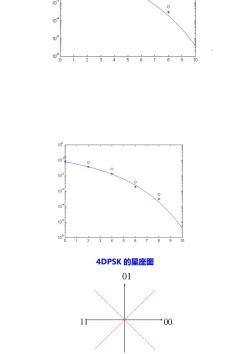
10 109 10 106 0 1 234567 8 9 10 10 10 o 102 103 0 109 105 1 3 6 8 9 10 4DPSK的星座图 01 - 00 -x-w -

semilogy(SNRindB1,smld_bit_err_prb,'*'); hold semilogy(SNRindB1,smld_symbol_err_prb,'o'); semilogy(SNRindB2,theo_err_prb,'-'); 4DPSK 的星座图 11 00 1001

4DPSK的编码规则 码元 11 01 10 11 11 01 △0 元 π/2 3π/2 元 元 π/2 π 3π/2 元 0 元 3π/2 4DPSK的蒙特卡罗仿真 function [p]=cm_sm34(snr_in_dB) N=10000: E=1; snr=10^(snr_in_dB/10); sgma=sqrt(E/(4*snr)); for i=1:2*N, temp=rand; if (temp<0.5), dsource(i)=0; else dsource(i)=1; end; end; mapping=[0 1 3 2]; M=4: [diff_enc_output]=cm_dpske(E,M,mapping,ds ource):%通过E(能量)M(进制数)mapping(星 座图)%desouce（信源)得到两个正交的矢量 for i=1:N [n(1)n(2)]=gngauss(sgma);

4DPSK 的编码规则 码元 11 01 10 11 11 01 Δφ π π/2 3π/2 π π π/2 φ π 3π/2 π 0 π 3π/2 4DPSK 的蒙特卡罗仿真 function [p]=cm_sm34(snr_in_dB) N=10000; E=1; snr=10^(snr_in_dB/10); sgma=sqrt(E/(4*snr)); for i=1:2*N, temp=rand; if (temp<0.5), dsource(i)=0; else dsource(i)=1; end; end; mapping=[0 1 3 2]; M=4; [diff_enc_output]=cm_dpske(E,M,mapping,ds ource);%通过 E(能量）M（进制数）mapping（星 座图）%desouce（信源）得到两个正交的矢量 for i=1:N [n(1) n(2)]=gngauss(sgma);