《通信原理实验》课程电子教案（PPT讲稿）MATLAB与通信仿真（英文）Chapter 4 Baseband Digital Transmission（Multidimensional Signals）

Baseband Digital Transmission Multidimensional Signals

Baseband Digital Transmission Multidimensional Signals

Multidimensional Vs.Multiamplitude Multiamplitude signal is One-dimensional 00 01 10 11 -3d -d 3d With One basis signal:g(t) Multidimensional signal Can be defined using multidimensional orthogonal signals

Multidimensional Vs. Multiamplitude ◼ Multiamplitude signal is One-dimensional ◼ With One basis signal: g(t) ◼ Multidimensional signal ◼ Can be defined using multidimensional orthogonal signals -3d -d d 3d 00 01 10 11

Multidimensional Orthogonal Signals Many ways to construct In this text,Construction of a set of M=2k waveforms s(t),i=1,2,.,M-1 Mutual Orthogonality ■ Equal Energy Using Mathematics ∫s,(0s0dh=56k,i,k=0,l,M-1 where Kronecker delta is 0,i≠k

Multidimensional Orthogonal Signals ◼ Many ways to construct ◼ In this text, Construction of a set of M=2k waveforms si (t), i=1,2,.,M-1 ◼ Mutual Orthogonality ◼ Equal Energy ◼ Using Mathematics ◼ where Kronecker delta is 0 ( ) ( ) , , 0,1,., 1 T i k ik s t s t dt i k M =  = −   1, 0, ik i k i k   = =   

Example of M=22 Multiamplitude Vs.Multidimensional 3d S3 A1So S1 S2 S3 S2 -d S1 -3d 50 All signal has identical energy 3=0h-=01M- See figure 4.27,page 202,for signal constellation

Example of M=22 ◼ Multiamplitude Vs. Multidimensional ◼ All signal has identical energy ◼ ◼ See figure 4.27, page 202, for signal constellation s3 s2 s1 s0 T 3d d -d -3d s0 s1 s2 s3 T A 2 2 0 ( ) , , 0,1,., 1 T i A T s t dt i k M M  = = = − 

Receiver for AWGN Channe Received signal from AWGN channel ■r()=S,(t)+(t),m=0,l,M-l,0≤t≤T White Gaussian process With power spectrum No/2 Receiver decides which of M signal waveform was transmitted by observing r(t) Optimum receiver minimize Probability of Error

Receiver for AWGN Channel ◼ Received signal from AWGN channel ◼ ◼ Receiver decides which of M signal waveform was transmitted by observing r(t) ◼ Optimum receiver minimize Probability of Error ( ) ( ) ( ), 0,1,., 1, 0 i r t s t n t m M t T = + = −   White Gaussian process With power spectrum N0 /2

Optimum Receiver for AWGN Channel Needs M Correlators (or Matched Filters) So(t) Samples at t=T r(t) [.dr SM-1(t) Detector Oytput Decision .od rM-1 5=∫0r0s,()d,i=0,l,M-1

Optimum Receiver for AWGN Channel ◼ Needs M Correlators (or Matched Filters) 0 ( ) ( ) , 0,1,., 1 T i i r r t s t dt i M = = −  0 ( ) t d  r(t) s0(t) Samples at t=T 0 ( ) t d  sM-1(t) Detector Output Decision r0 rM-1

Signal Correlators Let so(t)is transmitted (dt+[so(n()dt =+n ■5=∫rus,)dh=s,④+n0}s,0M -ss (di+s.(n()di=ni Orthogonal Noise component(Gaussian Process) Zero mean and Variance o-)

Signal Correlators ◼ Let s0 (t) is transmitted ◼ ◼ ◼ Noise component (Gaussian Process) ◼ Zero mean and Variance 0 0 0 0 0 0 2 0 0 0 0 0 ( ) ( ) { ( ) ( )} ( ) ( ) ( ) ( ) T T T T r r t s t dt s t n t s t dt s t dt s t n t dt n = = + = + =  +     0 0 0 0 0 0 0 ( ) ( ) { ( ) ( )} ( ) ( ) ( ) ( ) ( ) , 0 T T i i T T i i i r r t s t dt s t n t s t dt s t s t dt s t n t dt n i = = + = + =      Orthogonal 2 2 2 0 0 0 ( ) ( ) 2 2 T i i N N  E n s t dt  = = = 

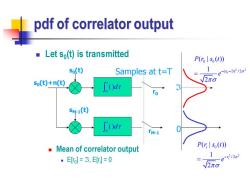
pdf of correlator output Let so(t)is transmitted P(rolso(t)) 5o(t) Samples at t=T 1 -e-y12a2 so(t)+n(t) 2πo SM-1(t) rM-1 Mean of correlator output P(rls(t)) ·Etl=3,E=0 1-e12o √2π0

pdf of correlator output ◼ Let s0 (t) is transmitted ◼ Mean of correlator output ◼ E[r0 ] = , E[ri ] = 0 0 ( ) t d  s0(t)+n(t) s0(t) Samples at t=T 0 ( ) t d  sM-1(t) r0 rM-1 2 2 0 0 0 ( ) / 2 ( | ( )) 1 2 r P r s t e    − − = 2 2 0 / 2 ( | ( )) 1 2 i i r P r s t e    − = 0 

Optimum Detector Let so(t)is transmitted The probability of correct decision Is probability that ro>i ■P=P(G>5,6>2,6>rM-) The average probability of symbol error ■PM=1-P=1-P(%>5,%>3,6>M-1) =-0w圳。9 For M=2 case(Binary Orthogonal signal) 月=X臣3，=36n

Optimum Detector ◼ Let s0 (t) is transmitted ◼ The probability of correct decision ◼ Is probability that r0 > ri ◼ ◼ The average probability of symbol error ◼ ◼ For M=2 case (Binary Orthogonal signal) ◼ 0 1 0 2 0 1 ( , ,., ) P P r r r r r r c M =    − 2 0 0 1 0 2 0 1 1 ( 2 / ) / 2 1 1 ( , ,., ) 1 {1 [1 ( )] } 2 M c M M y N P P P r r r r r r Q y e dy  −  − − −  − = − = −    = − −  2 0 ( ), b P Q for binary b N  =  = 

More on Probability error Average probability of symbol error ■ Same even if s(t)is changed Numerically evaluation of integral Converting probability of symbol error to probability of a binary digit error 2- PM 2-1 Symbol error probability Bit error probability ■Figure4.29page206 ■AsM→64，we need small SNR to get a given probability of error

More on Probability error ◼ Average probability of symbol error ◼ Same even if si (t) is changed ◼ Numerically evaluation of integral ◼ Converting probability of symbol error to probability of a binary digit error ◼ ◼ Figure 4.29 page 206 ◼ As M→64, we need small SNR to get a given probability of error 1 2 2 1 k b M k P P − = − Symbol error probability Bit error probability