《机械原理》课程授课教案（讲义）圆向量函数相关补充内容

1.2圆向量函数简介 一、圆向量函数定义 如图1，设平面直角坐标系XOY中向量工，模为L,方向用单位向量表示。E的方 向由L与+X轴之间的有向角日确定（日自十X轴逆时针度量为正，顺时针度量为负）。 若e的有向角B随时间而变化，则e是B的 函数，记为e(g)。显然向径e(0)的端点必 在半径为1的圆周上，所以单位向量（⊙）称 g(0)-(90°+0 为有向角日的圆向量函数 00°+8 同理，取与e(@垂直的单位向量 e90°+)，该单位向量与+X轴的有向角 为(90°+0)，与+Y轴的有向角为0。将这 个单位向量记为g(@)=e90°+).显然 g@)也是有向角日的圆向量函数。 图1 由图1：e0)=cos0.i+sin0.j g(0)=e(90°+)=-sm6.i+cos0.j 二、圆向量函数常用运算法则 圆向量函数是随有向角而变化的单位向量，其运算与一般向量之间的运算相同。下面是 圆向量函数的常用运算法则。 2(0).i=cos0 e(0).j=sin e(0)e(0)=g0)a)=l e(0)g0)=0 e(0)-e(0)=cos(0-0) g(e)-c(e)=e(90+a)-e(e)=sin(e-a) 1.3圆向量函数用于平面机构运动分析

1.2 圆向量函数简介 一、圆向量函数定义 如图 1，设平面直角坐标系 XOY 中向量 L  ，模为 L ，方向用单位向量 e  表示。 e  的方 向由 L  与＋ X 轴之间的有向角  确定（  自＋ X 轴逆时针度量为正，顺时针度量为负）。 若 e  的有向角  随时间而变化，则 e  是  的 函数，记为 e( )  。显然向径 e( )  的端点必 在半径为 1 的圆周上，所以单位向量 e( )  称 为有向角  的圆向量函数。 同理，取与 e( )  垂直的单位向量 e(90 +)  ，该单位向量与＋ X 轴的有向角 为 (90 +) ，与＋ Y 轴的有向角为  。将这 个单位向量记为 g() = e(90 +)   。显然 g()  也是有向角  的圆向量函数。 由图 1： e( ) i j     = cos  + sin   g( ) e( ) i j      = 90 + = −sin   + cos  二、圆向量函数常用运算法则 圆向量函数是随有向角而变化的单位向量，其运算与一般向量之间的运算相同。下面是 圆向量函数的常用运算法则。 e( )i = cos   e( ) j = sin    e() e() = g() g() =1     e() g() = 0   ( ) ( ) ( ) 1 2 1 2 e   e  = cos  −   ( ) ( ) ( ) ( ) ( ) 1 2 1 2 2 1 g   e  = e 90 +  e  = sin  −     1.3 圆向量函数用于平面机构运动分析 图 1

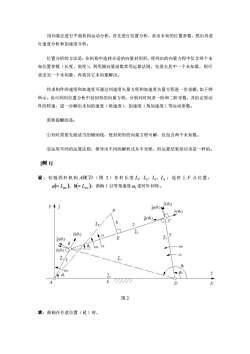
用向量法进行平面机构运动分析，首先进行位置分析，求出未知的位置参数，然后再进 行速度分析和加速度分析！ 位置分析的方法是：在机构中选择合适的向量封闭形，使列出的向量方程中仅含两个未 知位置参数（长度、角度）。利用圆向量函数常用运算法则，先消去其中一个未知量，则可 求出另一个未知量，再将其它未知量解出。 待求构件的速度和加速度可通过列速度矢量方程和加速度矢量方程进一步求解，如下例 所示。也可利用位置分析中封闭形的向量方程，分别对时间求一阶和二阶导数，并给定原动 件的转速，进一步解出未知的速度（角速度）、加速度（角加速度）等运动参数。 需要提醒的是： ①有时需要先做适当的辅助线，使封闭形的向量方程可解，仅包含两个未知数。 ②运用不同的运算法则，推导出不同的解析式并不奇怪，但运算结果却应该是一样的 例 设：较链四杆机构ABCD(图2)各杆长度LL2、LL4:连杆上F点位置： (=LsE人b(=Lr):曲柄1以等角速度，逆时针回转。 )ua) 2(0: (0) b a 图2 求：曲柄在任意位置（日）时

用向量法进行平面机构运动分析，首先进行位置分析，求出未知的位置参数，然后再进 行速度分析和加速度分析。 位置分析的方法是：在机构中选择合适的向量封闭形，使列出的向量方程中仅含两个未 知位置参数（长度、角度）。利用圆向量函数常用运算法则，先消去其中一个未知量，则可 求出另一个未知量，再将其它未知量解出。 待求构件的速度和加速度可通过列速度矢量方程和加速度矢量方程进一步求解，如下例 所示。也可利用位置分析中封闭形的向量方程，分别对时间求一阶和二阶导数，并给定原动 件的转速，进一步解出未知的速度（角速度）、加速度（角加速度）等运动参数。 需要提醒的是： ①有时需要先做适当的辅助线，使封闭形的向量方程可解，仅包含两个未知数。 ②运用不同的运算法则，推导出不同的解析式并不奇怪，但运算结果却应该是一样的。 [例 1] 设 ：铰链四杆机构 ABCD （图 2）各杆长度 L1、L2、L3、L4 ；连杆上 F 点位置： ( ) ( ) a = LBE 、b = LEF ；曲柄 1 以等角速度 1 逆时针回转。 图 2 求：曲柄在任意位置（ 1 ）时

①构件2、3的位置0，、日· ②构件2、3的角速度，、，角加速度6、6 ③连杆BC上F点的位置、速度、加速度。 解：取AD为十X轴方向建立直角坐标系XAY。沿X、Y轴的单位向量分别是i、j。 (一)位置分析：求、8，X、YF 做辅助线BD,先求日、L,再求日、，X、Y,如图2所示。 (A)向量三角形ABD中，当各边向量取图2所示方向时，有乙=乙，+乙，即 L,e(0)=-L,i+L·e(g) (① 式中，但)0)分别是i,、i,的单位向量，日.、g是有向角。 )j/)i,得 a,=arctan[Lsin/亿，cos8-L】 -a ①)0)，得 L.=L cos(0,-0)-L.cos0. (1-b) (B)向量三角形DBC中，有乙=乙，+乙2，即 Le(e)=Le(e)+L(e) (2) 式中，()、e(8)分别是3、,的单位向量，、是有向角 (②)式两边数学平方并整理，得 cos(0.-0)=(-)/2LL,) 则 0;=0,-arccos)/(L) (2-a (2)式移项，得 L2·eg)=Le(a)-Leg.) (2) (2)式两边数学平方并整理，得

①构件 2、3 的位置 2 、3 。 ②构件 2、3 的角速度 2 、3 ，角加速度 2  、 3  。 ③连杆 BC 上 F 点的位置、速度、加速度。 解：取 AD 为＋ X 轴方向建立直角坐标系 XAY 。沿 X 、Y 轴的单位向量分别是 i  、 j  。 （一）位置分析：求 2 、3 ， XF 、YF 做辅助线 BD ，先求 v 、 Lv ，再求 2 、3 ， XF 、YF ，如图 2 所示。 （A） 向量三角形 ABD 中，当各边向量取图 2 所示方向时，有 Lv L4 L1    = + ，即 ( ) ( )  4 1 1 L e L i L e v v     = −  +  (1) 式中， ( ) v e   、 ( ) 1 e  分别是 Lv  、 L1  的单位向量， v 、1 是有向角。 ( ) j ( ) i   1  1  ，得  ( ) 1 1 1 1 4 v = arctan L sin  L cos − L (1− a) ( ) ( ) v e   1  ，得 ( ) Lv L v  L v cos cos = 1 − 1 − 4 (1− b) （B） 向量三角形 DBC 中，有 L3 Lv L2    = + ，即 ( ) ( ) ( ) 3 3  2 2 L e L e L e v v     =  +  (2) 式中， ( ) 3 e  、 ( ) 2 e  分别是 L3  、 L2  的单位向量， 3 、2 是有向角。 (2) 式两边数学平方并整理，得 ( ) ( ) ( ) v L L Lv L2Lv 2 2 2 2 cos  −2 = 3 − − 2 则 ( ) ( ) v L L Lv L2Lv 2 2 2 2 2 =  − arccos 3 − − 2 (2 − a) (2) 式移项，得 ( ) ( ) ( ) v v L e  L e  L e      =  −  2 2 3 3 (2') (2') 式两边数学平方并整理，得

cos(8-8)=(2-)/2L4) 则 0=0.-arccos/(LL)] (2-b) (C)向量封闭形ABEF中，有ie=乙+a+b 即 Lse0)=Le0)+ae0,)+be90°+0) 式中，e(0)是e的单位向量，0，是有向角。 分别作(3)i和(3)，得F点的位置坐标为： X=L cos +acos0-bsin 3-a Y =Lsin 0 +asin0,+bcos, 3-b) (二)速度分析：求0、回，x、” 约定角速度0逆时针方向为正，推导公式。若0为顺时针方向，以负值代入：若求得 某构件的)为负值，则表示该构件转动方向为顺时针方向。 e=下g+c Lg(0)=oLg(a)+0Lg(0) 列 为求出，作(4)(@)，得 0=a,4sin(g-8)+o,↓2sn(g-8) =-o L sin (e-e)L sin (e-e) 4-a 同理(4)e(8),解得 =-L sin(0-a)/sin (-0.) (4-b) 将B-a)式对时间求一阶导数，得连杆BC上F点的速度 =-1sin -(asin e:+bcose.)o. 6-a Vrr=1 cos+(acos6-bsin )a 6-b)

( ) ( ) ( ) v L L Lv L3Lv 2 2 3 2 cos  −3 = 2 − − 2 则 ( ) ( ) v L L Lv L3Lv 2 2 3 2 3 =  − arccos 2 − − 2 (2 −b) （C） 向量封闭形 ABEF 中，有 LF L a b     = 1 + + 即 ( ) ( ) ( ) ( )  1 1 2 90 +2 L  e = L  e + a  e + b e  F F     (3) 式中， ( ) F e   是 LF  的单位向量，  F 是有向角。 分别作 ( ) i  3  和 ( ) j  3  ，得 F 点的位置坐标为： 1 1 2 2 XF = L cos + acos −bsin (3− a) 1 1 2 2 YF = L sin + asin +bcos (3−b) （二）速度分析：求 2 、3 ， FX v 、 FY v 约定角速度  逆时针方向为正，推导公式。若  为顺时针方向，以负值代入；若求得 某构件的  为负值，则表示该构件转动方向为顺时针方向。 C B CB v v v    = + 即 ( ) ( ) ( ) 3L3 g 3 1L1 g 1 2L2 g 2     =  +  (4) 为求出 2 ，作 ( ) ( ) 4 3 e   ，得 ( ) ( ) 1 1 3 1 2 2 3 2 0 = L sin  − + L sin  − 则 ( )  ( ) 2 1 1 3 1 2 3 2  = − L sin  − L sin  − (4 − a) 同理 ( ) ( ) 4 2 e   ，解得 ( )  ( ) 3 1 1 2 1 3 3 2  = − L sin  − L sin  − (4 −b) 将 (3− a) 式对时间求一阶导数，得连杆 BC 上 F 点的速度： ( ) 1 1 1 2 2 2 vFX = −L sin − asin + bcos  (5− a) ( ) 1 1 1 2 2 2 vFY = L cos + acos −bsin  (5 −b)

(三)加速度分析：求62、6，ax、a 约定角加速度ε逆时针为正，推导公式。 由记+或=aa+n+g,得 -aL0)+eg0,)=-oL·0)-L20)+e2g0）(6) (6)e(8),整理得 E:=[oiL cos(0,-0)+L cos(0,-0)-oLML sin (0-0.)(6-a) (⑥(8，)，整理得 6=回Lcos0-)+o凸-ojLcosl0,-,sn(g-8,】6-b) 则a=a+a论=-oLe(g)+e,4g0) =-(6Lsin +L cos0)i+(6L cos0,-ojLsin )j 将5-a小、5-b)式对时间求一阶导数，得连杆BC上F点加速度： arx =-0L cos+(bsin 0 -acos )o-(asin 0 +bcos0 )s2 (7-a) ary =-0L sin e-(asin0 +bcose)o+(acos0-bsin 0)s (7-b) 如果编制计算机程序，代入计算运动参数的上述解析式，并在曲柄回转一周（即机构的 一个运动循环)的范围内，取一系列（值，便可求出相应位置的运动参数，绘出运动参数 随O变化的曲线图，根据F点的坐标可在屏幕上或打印纸上绘出F点的运动轨迹形成的连 杆曲线。 例2引设：图3所示导杆机构，已知各杆尺寸，曲 柄1以等角速度逆时针方向回转。 a)1 求：曲柄在任意位置日时，输出构件3的运动参数 8, 、6,构件3上B点的运动参数vg、aa 解：（一）位置分析：求8，L D

（三）加速度分析：求 2  、 3  ， FX a 、 FY a 约定角加速度  逆时针为正，推导公式。 由 n t n t aC aC aB aCB aCB      + = + + ，得 ( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 2 1 1 2 2 3 3 3 3 3 1 2 3 L e   L g   L e   L e   L g       −  +  = −  −  +  (6) ( ) ( ) 6 3 e   ，整理得  ( ) ( )   ( ) 3 2 3 2 2 2 3 2 3 2 1 3 1 2 2 2 1  =  L cos  − + L cos  − − L L sin  − (6 − a) ( ) ( ) 6 2 e   ，整理得  ( ) ( )  ( ) 3 3 2 3 3 2 2 2 3 2 1 2 1 2 2 3 1  =  L cos  − + L − L cos  − L sin  − (6 −b) 则 ( ) ( ) 3 3 3 3 3 2 3 n t aC aC aC  L e   L g       = + = −  +  ( L L ) i ( L L ) j   = − +  + −  3 3 2 3 3 3 3 3 3 2 3 3 3 3  sin   cos  cos  sin  将 (5− a)、 (5 −b) 式对时间求一阶导数，得连杆 BC 上 F 点加速度： ( ) ( ) 2 2 2 2 1 1 2 2 2 2 1 a  L cos bsin  acos  asin  bcos  FX = − + − − + (7 − a) ( ) ( ) 2 2 2 2 1 1 2 2 2 2 1 a  L sin  asin  bcos  acos bsin   FY = − − + + − (7 −b) 如果编制计算机程序，代入计算运动参数的上述解析式，并在曲柄回转一周（即机构的 一个运动循环）的范围内，取一系列 1 值，便可求出相应位置的运动参数，绘出运动参数 随 1 变化的曲线图，根据 F 点的坐标可在屏幕上或打印纸上绘出 F 点的运动轨迹形成的连 杆曲线。 [例 2] 设：图 3 所示导杆机构，已知各杆尺寸，曲 柄 1 以等角速度 1 逆时针方向回转。 求：曲柄在任意位置 1 时，输出构件 3 的运动参数 3 、 3  ，构件 3 上 B 点的运动参数 B v 、 B a 。 解：（一）位置分析：求 3 ， LDA

在向量△DOA中，有 h.j+Le()=Loa-@(0) ) )j/0)i,解得 0 arctan[h/(L cose)+tan] 图3 )e(g,得 Lpa hsin+cos(e-0) (二)速度分析：求，Vg B=下+币B2,即 @,Log(0)=0Lg(0)+vxe(0) 2) (2)g),解得 o=oL cos(0,-g)/Lo (2)0),解得 2=-a,4sn(g-a) 则ya=m,L3ge)=o,L(sin6·i+cos8j)=-a,L3sm8·i+,Lcos8·j (三)加速度分析：求6，ag da+dg=d42+aB2+a,即 -oLae(a)+c,log0）=-L·e8)+42·(e,)-2ya,'ge）)3) 式中以，=0，这是因为构件2和3之间组成移动副，只有相对移动，没有相对转动。 ③)g(8,),解得 6,=-Lsn(g-0,)+2,/Ln ③)e(0),解得 aj2=oiL cos(0-0)-@Lp 则aa=a8+a。=-o四L3e(%)+cL3·g(g) =-L,(acos8+6sma）i-Lasn0-6cos8）j

在向量 DOA 中，有 ( ) ( ) 1 1 3 h j L e L e DA     +  =  (1) ( ) j ( ) i   1  1  ，解得  ( )  3 1 1 1  = arctan h L cos + tan ( ) ( ) 1 3 e   ，得 ( ) 3 1 3 1 LDA = hsin  + L cos  − （二）速度分析：求 3 ， B v A3 A2 A3A2 v v v    = + ，即 ( ) ( ) ( ) 3 3 1 1 1 32 3 L g L g v e DA     =  +  (2) ( ) ( ) 2 g 3   ，解得 ( ) 3 1L1 3 1 LDA  = cos  − ( ) ( ) 2 3 e   ，解得 ( ) 32 1 1 3 1 v = − L sin  − 则 v L g( ) L ( i j) B    =  = −  +  3 3 3 3 3 3 3    sin  cos L i L j   = −  +  3 3 3 3 3 3  sin   cos （三）加速度分析：求 3  ， B a k 3 2 r 2 3 2 t 3 n aA3 aA aA aA A aA A      + = + + ，即 ( ) ( ) ( ) ( ) ( ) 3 3 2 2 3 r 1 1 3 2 2 3 3 3 1 2 3 LDA e   LDA g   L e  a e  2v  g       −  +  = −  +  −  (3) 式中 2 =3 ，这是因为构件 2 和 3 之间组成移动副，只有相对移动，没有相对转动。 ( ) ( ) 3 g 3   ，解得  ( )  LDA L v 1 1 3 32 2 2  3 = − 1 sin  − + 2  ( ) ( ) 3 3 e   ，解得 ( ) a L LDA 2 1 1 3 3 2 1 r 32 = cos  − − 则 ( ) ( ) 3 3 3 3 3 2 3 n t aB aB aB  L e   L g       = + = −  +  L ( ) i L ( ) j   = − +  − −  3 3 3 2 3 3 3 3 3 2 3 3  cos  sin   sin   cos 图 3