南阳师范学院：《高等数学》课程教学课件（同济第六版）第七章 微分方程的基本概念 7.6 高阶线性微分方程

第六节 高阶线性微分方程 一.二阶线性微分方程举例 二.线性微分方程的解的结构 1

1 一.二阶线性微分方程举例 二.线性微分方程的解的结构 第六节 高阶线性微分方程

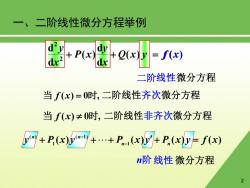
一、二阶线性微分方程举例 dy dx2 +P(x 2(wy =f(x) 二阶线性微分方程 当f(x)=0时，二阶线性齐次微分方程 当f(x)≠0时，二阶线性非齐次微分方程 y+P()y.+P.)y+P.(x)y-fx) n阶线性微分方程 2

2 二阶 ( ) ( ) d d ( ) d d 2 2 Q x y f x x y P x x y    当 f (x)  0时, 二阶线性齐次微分方程 当 f (x)  0时, 二阶线性非齐次微分方程 微分方程 ( ) ( ) ( ) ( ) 1 ( 1) 1 ( ) y P x y P n x y P n x y f x n n          线性微分方程 f (x) n阶 线性 一、二阶线性微分方程举例

二、线性微分方程的解的结构 齐次：y”+P(x)y+Q(x)y=0 (1) 定理1如果函数，(x)与y,(x)是方程1)的两个解 那么y=C1y,(x)+C2y(x)也是(1)的解(C1,C2是常数)， y=C11(x)+C22(x)一定是通解吗 注记：y=C1y1(x)+C2y2(x)不一定是所给二阶齐次 线性方程的通解

3 y  P(x) y  Q(x) y  定理1 ( ) ( ) (1) , 如果函数y1 x 与y2 x 是方程 的两个解 那么y C1 y1 (x) C2 y2 (x)也是(1)的 ( , ). C1 C2是常数 0 ( ) ( ) 1 1 2 2 y  C y x  C y x 一定是通解吗 (1) 二、线性微分方程的解的结构 解 齐次： 注记: y  C1 y1 (x)  C2 y2 (x) 不一定是所给二阶齐次 线性方程的通解

设，y2,,yn为定义在区间I内的n个函数. 如果存在个不全为零的常数，使得当x在该区间 内恒等式成立 k1y1+k22+…+knyn三0 那么称这n个函数在区间内线性相关。 否则称线性无关. 如 1,cos2x,sin2x(x∈(-oo,+oo)线性相关 取k1=1,k2=k3=-1,有恒等式 1-cos2 x-sin2x=0

4 n y , y , , y 设 1 2  0 k1 y1  k2 y2  kn yn  线性相关. 否则称 线性无关. 如 1 cos ,sin ( ( , )) 2 2 ， x x x   线性相关 取k1  1,k2  k3  1,有恒等式 1 cos sin 0 2 2  x  x  内恒等式成立 如果存在n个不全为零的常数, 使得当x在该区间 那么称这n个函数在区间I内 为定义在区间I内的n个函数

若在上有 y(x) y'2(x) ≠常数则函数y(x)与y2(x) 在1上线性无关： e*,ex,e2x(x∈(-oo,十o)线性无关

线性无关. ( ) ( ) 2 1 y x y x 若在I上有  常数, 则函数y1 (x)与y2 (x) 在I上 e x , e x , e 2 x (x(,)) 线性无关

y"+P(x)y'+2(x)y=0(1) 定理2如果函数y,()与y(x)是方程(1)的 两个线性无关的特解，那么y=C1y1(x)+C2Jy2(x) 也是(1)的通解， 例如y”+y=0,y1=c0sx,2=sinx, 且2=tan≠常数， y 通解：y=C1c0sx+C2Sinx. 6

6 定理2 ( ) ( ) 1 1 2 2 y  C y x  C y x y  P(x) y  Q(x) y  0 (1) 两个线性无关的特解,那么 也是(1)的通解. 如果函数y1 (x)与y2 (x)是方程(1)的 例如 y  y  0, cos , y1  x x y y tan 1 2 且  cos sin . 通解： y  C1 x C2 x  常数, sin , y2  x

推论如果函数y(x),y2(x),,yn(x)是n阶 齐次线性方程 y(m+P(x)y(-D+..+P(x)y'+P(x)y=0 的n个线性无关的解，那么，此方程的通解为 y=Ciy](x)+C2yz(x)+...+Cnyn(x), 其中C1,C2,…,Cn为任意常数

7 推论 是 n 阶 齐次线性方程 ( ) 1 ( ) ( ) 0 ( 1) 1 ( )         y P x y P x y P x y n n n n  的 n 个线性无关的解, 那么, 此方程的通解为 ( ) ( ) ( ), 1 1 2 2 y C y x C y x C y x    n n 其中 C C Cn , , , 1 2  为任意常数. ( ), ( ), , ( ) 如果函数 y1 x y2 x  yn x

y"+P(x)y'+Q(x)y=0(1) 定理3 设y*是二阶非齐次线性微分方程 y"+P(x)y'+2(x)y=f(x) (2) 的一个特解，Y是与(2)对应的齐次方程(1)的通解， 那么y=Y+y是二阶非齐次线性微分方程(2)的 通解. 注记：为了非齐次线性方程的通解，只要求得： 非齐次线性方程的一个特解和对应齐次线性方程 的通解

8 定理3 y  P(x) y  Q(x) y   设y 的一个特解,  那么y  Y  y 注记：为了求 非齐次线性方程的一个特解 和对应齐次线性方程 只要求得: 的通解. y  P(x) y  Q(x) y  0 (1) f (x) (2) 非齐次线性方程的通解, Y 是与(2)对应的齐次方程(1)的通解, 是二阶非齐次线性微分方程(2)的 通解. 是二阶非齐次线性微分方程

如方程y”+y=x2是二阶非齐次线性方程 己知Y=C1cosx+C2sinx是y”+y=0的通解 y*=x2-2是所给方程的一个特解. 所以y=Y十y* =C cosx+C2 sinx+x2-2 是非齐次方程的通解. 9

9 2 方程y  y  x 已知 Y  C1 cos x C2 sinx y  y  0 的通解. 2 2    y x 是所给方程的一个特解. 是非齐次方程的通解. y  Y  y  如 是二阶非齐次线性方程.  C1 cos x C2 sinx 2 2  x  是 所以

y"+P(x)Jy'+2(x)y=f(x)(2) 定理4 设非齐次方程(2)的右端f(x)是几个 函数之和，如y"+P(x)y'+(x)y=f1(x)+f(x) 而y与y分别是 Jy"+P(x)y'+2()y=f(x) y"+P(x)y'+Q(x)y=f(x) 的特解，那么+y2就是原方程的特解 解的叠加原理

10 解的叠加原理 定理4 如y  P(x)y  Q(x) y  而y1  与y2  分别是 ( ) ( ) ( ) y  P x y  Q x y  f1 x ( ) ( ) ( ) y  P x y  Q x y  f2 x   1  2 y y y  P(x)y  Q(x)y  f ( x)) (2) f1 (x) ( ) 函数之和, f2 x 的特解, 那么 就是原方程的特解. 设非齐次方程(2)的右端f (x)是几个