南阳师范学院：《概率统计》课程教学资源（讲稿）二、随机变量及其分布

南阳师范学院 Nanyang Normal University 数学与镜计学院 第三章 随机变量及其分布 学习目标 理解随机变量的概念、掌握离散型随机变量及概率函数（分布列）的概念和 性质、掌握连续型随机变量及概率密度的概念和性质，理解分布函数 的概念和性质，会利用概率分布计算有关事件的概率，掌握二项分布 、泊松(Poissor)分布、正态分布，了解均匀分布与指数分布，会求简 单随机变量函数的概率分布

School of Maths and Statistics 第三章 随机变量及其分布 学习目标 理解随机变量的概念、掌握离散型随机变量及概率函数 (分布列 )的概念和 性质、掌握连续型随机变量及概率密度的概念和性质，理解分布函数 的概念和性质，会利用概率分布计算有关事件的概率，掌握二项分布 、泊松(Poisson)分布、正态分布，了解均匀分布与指数分布，会求简 单随机变量函数的概率分布

南阳师范学院 Nanyang Normal University 数学与统学院 第一节随机变量及分布函数 在前面的学习中，我们用字母A、B、C..表示事件，并 视之为样本空间2的子集； 对等可能概型，主要研究了用排列组合手段计算事件的概率 本章，将用随机变量表示随机事件，以便采用高等数学 的方法描述、研究随机现象

School of Maths and Statistics 第一节 随机变量及分布函数 在前面的学习中,我们用字母A、B、C...表示事件，并 视之为样本空间Ω的子集； 对等可能概型，主要研究了用排列组合手段计算事件的概率 . 本章，将用随机变量表示随机事件，以便采用高等数学 的方法描述、研究随机现象

南阳师范学院 Nanyang Normal University 数学与镜计学院 基本思想 将样本空间数量化，即用数值来表示试验的结果 有些随机试验的结果可直接用数值来表示. 例如：在掷骰子试验中，结果可用1,2,3,4,5,6来表示 有些随机试验的结果不是用数量来表示，但可数量化： 例如：掷硬币试验，其结果是用汉字“正面”和“反面”来表示的 可规定：用1表示“正面朝上”用0表示“反面朝上

School of Maths and Statistics 基本思想 将样本空间数量化,即用数值来表示试验的结果 有些随机试验的结果可直接用数值来表示. 例如: 在掷骰子试验中,结果可用1,2,3,4,5,6来表示. 例如: 掷硬币试验,其结果是用汉字“正面”和“反面”来表示的. 可规定: 用1表示 “正面朝上” 用 0表示“反面朝上”. 有些随机试验的结果不是用数量来表示，但可数量化

南阳师范学院 Nanyang Normal University 数学与统学院 例设箱中有10个球，其中有2个红球，8个球；从中任意 抽取2个，观察抽球结果 分析取球结果为：两个白球；两个红球；一红一白 如果用X表示取得的红球数，则X的取值可为0,1,2. 此时，“两只红球”=“X取到值2”，可记为{X=2} “一红一白”记为{X=1}, “两只白球”记为{X=0} 特点：试验结果数量化了，试验结果与数建立了对应关系

School of Maths and Statistics 例 设箱中有10个球，其中有2个红球，8个球；从中任意 抽取2个,观察抽球结果. 分析 取球结果为: 两个白球;两个红球;一红一白 特点：试验结果数量化了，试验结果与数建立了对应关系. 如果用X表示取得的红球数，则X的取值可为0，1，2. 此时， “两只红球”= “X取到值2”, 可记为 {X=2} “一红一白”记为 {X=1}, “两只白球”记为 {X=0}

南阳师范学院 Nanyang Normal University 数学与镜计学院 随机变量的定义 设随机试验的样本空间为Ω，如果对于每一 个样本点0∈①，均有唯一的实数 X(o) 之对应，称 X=X(O) 为样本空间2上 的随机变量 关于随机变量的注记： 1)它是一个变量， 2)它的取值随试验结果而改变， 3)随机变量在某一范围内取值，表示一个随机事件

School of Maths and Statistics 1) 它是一个变量， 2) 它的取值随试验结果而改变， 3）随机变量在某一范围内取值，表示一个随机事件. 随机变量的定义 关于随机变量的注记: 设随机试验的样本空间为Ω，如果对于每一 个样本点 ，均有唯一的实数 之对应，称 为样本空间Ω上 的随机变量. ω ∈Ω X ( ) ω X X = ( ) ω

南阳师范学院 Nanyang Normal University 数学与统学院 例如 某个灯泡的使用寿命X, X的可能取值为[0，+o). 某电话总机在一分钟内收到的呼叫次数Y. Y的可能取值为0,1,2,3，·. 在[0,1]区间上随机取点，该点的坐标X. X的可能取值为[0,1]上的全体实数

School of Maths and Statistics 某个灯泡的使用寿命X， 某电话总机在一分钟内收到的呼叫次数Y. 在[0，1]区间上随机取点，该点的坐标X. X 的可能取值为 [0,+ ∞). Y 的可能取值为 0，1，2，3，.... 例如 X 的可能取值为 [0，1]上的全体实数

南阳师范学院 Nanyang Normal University 数学与镜计学院 分布函数的定义 设X为一随机变量，则对任意实数x,(仪x)是一个随机事件 ，称 F(x)=P(X≤x) F(x)是一个普 为随机变量X的分布函数 通的函数 定义域为 (一∞，十∞)；值域为[0,1]

School of Maths and Statistics 设X为一随机变量,则对任意实数x，(X x)是一个随机事件 ，称 为随机变量 X 的分布函数. 定义域 为 （－∞，＋∞）；值域 为 ［０，１］. F(x)是一个普 通的函数！ () ( ) 分布函数的定义 F x PX x = ≤ ≤

南阳师范学院 Nanyang Normal University 数学与统学院 引进分布函数F(x)后，事件的概率都可以用 F(x)的函数值来表示. P(X≤b)=F(b) P (X>b)=1-P (X<b)=1-F(b) P(a<X≤b)=F(b)-F(a) P(a<X≤b)=P(X≤b)-P(X≤a)=F(b)-F(a)

School of Maths and Statistics 引进分布函数F(x)后，事件的概率都可以用 后，事件的概率都可以用 F(x)的函数值来表示 的函数值来表示. P（X ≤ b）=F(b) P（ab）=1﹣ P（X ≤ b）=1 - F(b) P（a<X ≤ b）=P(X ≤ b)-P(X ≤ a)= F(b)- F(a)

南阳师范学院 Nanyang Normal University 数学与镜计学院 分布函数的性质 F(x)是单调不减函数； 若x≤x2,则F(x)≤F(x2) Fx)处处左连续，即F(x-O)=F(x) 0≤F(x)≤1，且 F(-)=lim F(x)=0,F(+o)=lim F(x)=1 X>+00 F(-∞)=P{X<-o} 不可能事件 F(+o∞)=P{X<+0} 必然事件

School of Maths and Statistics 分布函数的性质 F(x)是单调不减函数； 0≤ F(x) ≤1, 且 ( ) lim ( ) 0, ( ) lim ( ) 1 x x F Fx F Fx →−∞ →+∞ −∞ = = +∞ = = 1 2 若 x ≤ x , 1 2 则Fx Fx ( ) ( ). ≤ F PX () { } −∞ = < −∞ 不可能事件 F PX () { } +∞ = < +∞ 必然事件 F(x)处处左连续，即 Fx Fx ( 0) ( ) − =

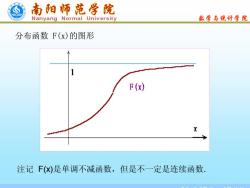
南阳师范学院 Nanyang Normal University 数学与统学院 分布函数F(x)的图形 F(x) 注记F(X)是单调不减函数，但是不一定是连续函数

School of Maths and Statistics 分布函数 F(x)的图形 注记 F(x)是单调不减函数，但是不一定是连续函数