南阳师范学院:《高等数学》课程教学课件(同济第六版)第七章 微分方程的基本概念 7.4 一阶线性微分方程

第四节一阶线性微分方程
第四节 一阶线性微分方程
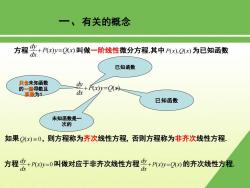
一、有关的概念 方程会+y=Qx)叫做一阶线性微分方程其中P,Q)为已知函数 已知函数 只含未知函数 的一阶导数且 +Py=Q 系数为1 dx 已知函数 未知函数是一 次的 如果Q()=0,则方程称为齐次线性方程,否则方程称为非齐次线性方程 方程密+代y-0叫做对应于非齐次线性方程密代-Q的齐次线性方程 dx
方程 P(x)y Q(x) dx dy 叫做一阶线性微分方程其中P x Q x ( ), ( ) 为已知函数. 一、有关的概念 P(x)y Q(x) dx dy 如果 Q x( ) 0 则方程称为齐次线性方程 否则方程称为非齐次线性方程 方程 P(x)y0 dx dy 叫做对应于非齐次线性方程 P(x)y Q(x) dx dy 的齐次线性方程 已知函数 已知函数 只含未知函数 的一阶导数且 系数为1 未知函数是一 次的

一、有关的概念 已知函 已知函数 数 +Pxy=O dx 只含未知函数 未知函数是一 的一阶导数且 次的 系数为1 例1:判断正误 (1) -xy=sinx是一阶线性微分方程 d (2) -x2y=sinx不是一阶线性微分方程, dx (3) 少-2少=0是一阶齐次线性微分方程。 dx x+1 (4) 少-2少=x+1)是一阶非齐次线性微分方程. dx x+1 (5) (x2+y2)dk-3d=0是一阶线性微分方程
一、有关的概念 P(x)y Q(x) dx dy 例 1:判断正误 (1) 2 sin dy x y x dx 是一阶线性微分方程 未知函数是一 次的 已知函数 只含未知函数 的一阶导数且 系数为1 已知函 数 (2) 2 sin dy y x y x dx 不是一阶线性微分方程 (3) 2 0 1 dy y dx x 是一阶齐次线性微分方程 (4) 5 2 2 1 1 dy y x dx x 是一阶非齐次线性微分方程 (5) 2 2 ( ) 0 x y dx xydy 是一阶线性微分方程

二、一阶齐次线性方程的解法 注记1:齐次线性方程会+咖=0是可分离变量的微分方程 定理1:一阶齐次线性方程票+-0的通解是 y=CeJ体(C=士eS)(积分中不再加任意常数). 注记2:解一阶齐次线性方程的步骤 第一步:分离变量:少=-Px, 第二步:两边积分得nl咋∫P(x)d+C, 第三步:求出y=CeP(C=±e9) 就是齐次线性微分方程的通解(积分中不再加任意常数)
二、一阶齐次线性方程的解法 注记 1:齐次线性方程 P(x)y0 dx dy 是可分离变量的微分方程 注记 2:解一阶齐次线性方程的步骤 第一步:分离变量: P x dx y dy ( ) 第二步:两边积分得 1 ln| y| P(x)dxC 就是齐次线性微分方程的通解(积分中不再加任意常数) 定理 1:一阶齐次线性方程 P(x)y0 dx dy 的通解是 ( ) 1 P(x)dx C y Ce Ce (积分中不再加任意常数) 第三步: 求出 ( ) 1 P(x)dx C y Ce Ce

三、一阶非齐次线性方程的解法一一常数变易法 定理2:一阶非齐次线性方程会+代ey-Q的通解为 y=CeJP+e JPxk∫ecxe在. 对应的齐次线性方 非齐次线性方程的特解 程通解
定理 2:一阶非齐次线性方程 P ( x ) y Q ( x ) dx dy 的通解为 y Ce e Q x e dx P x dx P x dx P x dx ( ) ( ) ( ) ( ) 三、一阶非齐次线性方程的解法---常数变易法 对应的齐次线性方 程通解 非齐次线性方程的特解

注记2求一阶非齐次线性方程的方法有两种 方法一:常数便易法—一步骤 第一步:求齐次线性方程+Py=0的通解y=CePw体(C=±eS) 第二步:将齐次线性方程通解中的常数换成x的未知函数),把y=xeP4 设想成非齐次线性方程的通解.代入非齐次线性方程求得(x) 第三步:将求得的)代入y(eha即可得到会+Py=Q的通解
注记 2 求一阶非齐次线性方程的方法有两种 方法一:常数便易法---步骤 第一步:求齐次线性方程 P(x)y0 dx dy 的通解 ( ) 1 P(x)dx C y Ce Ce 第二步:将齐次线性方程通解中的常数换成 x 的未知函数 u x( ) 把 P x dx y u x e ( ) ( ) 设想成非齐次线性方程的通解 代入非齐次线性方程求得 u x( ) 第三步:将求得的 u x( ) 代入 P x dx y u x e ( ) ( ) 即可得到 ( ) ( ) dy P x y Q x dx 的通解

阶非齐次线性方程密+Pe=Q)的通解y-Ce*+eA∫Xx)elrd 方法二:公式法 第一步:确定P(x),Q(x) 第二步:求∫P(x、era达与。(积分中不再加任意常数) 第三步:求∫Qx)eadk及ea咖Qxek(积分中不加任意常数) 第四步:求Cef+ea2prad在
一阶非齐次线性方程 P(x)y Q(x) dx dy 的通解 y Ce e Q x e dx P x dx P x dx P x dx ( ) ( ) ( ) ( ) 方法二:公式法 第一步:确定 P x Q x ( ), ( ) 第二步:求 P x dx ( ) 、 P x dx ( ) e 与 P x dx ( ) e (积分中不再加任意常数) 第三步:求 ( ) ( ) P x dx Q x e dx 及 ( ) ( ) ( ) P x dx P x dx e Q x e dx (积分中不加任意常数) 第四步:求 ( ) ( ) ( ) ( ) P x dx P x dx P x dx Ce e Q x e dx

可以使用公式 例2求方程会头+的通解 解:这是一个一阶非齐次线性方程。先求对应的齐次线性方程会升0的通解 分离变量得少-2血,积分得1nl2nlkx+1+C,即齐次线性方程的通解为y=C(x+ y x+l 用常数变易法把C换成u,即令y=(x+1),代入所给非齐次线性方程,得 (x+'W+20x+1M-2 中7+u=任+) 从而d=+12,两边积分得u-+2+C. 再把上式代入y=(x+)'中,即得所求方程的通解为 2 y=x+3+Cx+
例 2 求方程 2 5 ( 1) 1 2 x x y dx dy 的通解 解:这是一个一阶非齐次线性方程 先求对应的齐次线性方程 0 1 2 x y dx dy 的通解 分离变量得 1 2 x dx y dy ,积分得 1 ln 2ln 1 y x C ,即齐次线性方程的通解为 2 y C x 1 用常数变易法把C 换成 u 即令 2 y u x 1 ,代入所给非齐次线性方程 得 5 2 2 2 2 ( 1) 2( 1) ( 1) ( 1) 1 x u x u x u x x 从而 2 1 u (x1) 两边积分得 u x 2 C 3 ( 1) 3 2 再把上式代入 2 y u x 1 中 即得所求方程的通解为 2 2 7 ( 1) ( 1) 3 2 y x C x 可以使用公式
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第七章 微分方程的基本概念 7.3 齐次方程.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第七章 微分方程的基本概念 7.2 可分离变量的微分方程.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第七章 微分方程的基本概念 7.1 微分方程的基本概念.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十二章 无穷级数 12.4 函数展开成幂级数.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十二章 无穷级数 12.3 幂级数.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十二章 无穷级数 12.2 常数项级数的审敛法.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十二章 无穷级数 12.1 常数项级数的概念与性质.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.7 斯托克斯公式.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.6 高斯公式.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.5 对坐标的曲面积分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.4 对面积的曲面积分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.3 格林公式及其应用.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.2 对坐标的曲线积分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.1 对弧长的曲线积分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第五章 定积分及其应用 5.4 反常积分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第五章 定积分及其应用 5.3 定积分的换元法及分部积分法.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第五章 定积分及其应用 5.2 微积分基本公式.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第五章 定积分及其应用 5.1 定积分的概念与性质.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第三章 微分中值定理与导数的应用 3.7 曲率.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第三章 微分中值定理与导数的应用 3.6 函数图形的描绘.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第七章 微分方程的基本概念 7.5 可降阶的高阶微分方程.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第七章 微分方程的基本概念 7.6 高阶线性微分方程.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第七章 微分方程的基本概念 7.7 常系数齐次线性微分方程.pdf
- 南阳师范学院:《线性代数》课程教学课件(同济第五版)第一章 行列式(数学与统计学院:高景利).pdf
- 南阳师范学院:《线性代数》课程教学课件(同济第五版)第二章 矩阵及其运算.pdf
- 南阳师范学院:《线性代数》课程教学课件(同济第五版)第三章 矩阵的初等变换与线性方程组.pdf
- 南阳师范学院:《线性代数》课程教学课件(同济第五版)第四章 向量组的线性相关性.pdf
- 南阳师范学院:《线性代数》课程教学课件(同济第五版)第五章 相似矩阵及二次型.pdf
- 南阳师范学院:《概率统计》课程教学资源(讲稿)一、概率与事件.pdf
- 南阳师范学院:《概率统计》课程教学资源(讲稿)二、随机变量及其分布.pdf
- 南阳师范学院:《概率统计》课程教学资源(讲稿)四、随机变量的数字特征.pdf
- 南阳师范学院:《概率统计》课程教学资源(总结)1、随机事件及其概率.pdf
- 南阳师范学院:《概率统计》课程教学资源(总结)2、一维随机变量及其分布.pdf
- 南阳师范学院:《概率统计》课程教学资源(总结)3、二维随机变量及其分布.pdf
- 南阳师范学院:《概率统计》课程教学资源(总结)4、数字特征.pdf
- 南阳师范学院:《概率统计》课程教学资源(总结)5、统计部分.pdf
- 南阳师范大学:《线性代数》课程教学资源(练习题)第一章 练习题.pdf
- 南阳师范大学:《线性代数》课程教学资源(练习题)第二章 练习题.pdf
- 南阳师范大学:《线性代数》课程教学资源(练习题)第三章 练习题.pdf
- 南阳师范大学:《线性代数》课程教学资源(练习题)第四章 练习题.pdf
