南阳师范学院：《高等数学》课程教学课件（同济第六版）第五章 定积分及其应用 5.4 反常积分

§5.4反常积分 基本内容 一、无穷限的反常积分 二、无界函数的反常积分

一、无穷限的反常积分 二、无界函数的反常积分 §5.4 反常积分 基本内容

一、无穷限的反常积分 函数fx)在区间[4，+o)上连续，仑4， (若极限imf(x)d存在，则称这个极限 为f(x)在a,+o)上的反常积分，记作f(x)dc; 这时也称反常积分收敛； (2)若mf(x)不存在，则称反常积分 ∫fx)tc发散

一、无穷限的反常积分 函数f(x)在区间[a, )上连续，t>a, ( ) . a f x dx   发散 1   ( ) lim ( ) 若极限 存在，则称这个极限 t t a f x dx ( ) [ , ) ( ) ; a f x a f x dx   为 在 上的反常积分，记作 这时也称反常积分收敛； 2   ( ) lim ( ) 若 不存在，则称反常积分 t t a f x dx

一、无穷限的反常积分 fx)在(-o,]上的反常积分： ,∫a=limf)d. fx)在(-oo,+o)的反常积分： d-limmd

一、无穷限的反常积分 f(x)在(,b]上的反常积分: f(x)在(, )的反常积分: f x dx f x dx b t t b  ( ) lim  ( )   = . f x dx f x dx f x dx t t t t ( ) lim ( ) lim ( ) 0 0        = 

一、无穷限的反常积分 ·反常积分的计算 如果Fx)是fx)的原函数，则有 ∫f(x)d=[F(xl lim F(x)-F(a)

一、无穷限的反常积分 •反常积分的计算 如果F(x)是f(x)的原函数 则有 lim F(b) F(a) lim F(x) F(a) b x =  =    . ( ) a f x dx   [ ( )] F x a  =

一、无穷限的反常积分 ·反常积分的计算 类似地，有 f(x)dx=[F(x)F(b)-lim F(x), 例如， e'dx =[e"p=e-lim e"=1

一、无穷限的反常积分 类似地 有 f (x)dx [F(x) ] F(b) lim F(x) x b b   =  =    •反常积分的计算 0 x e dx  0 [ ]x e =  0 lim x x e e  =  =1 例如

一、无穷限的反常积分 ·反常积分的计算 类似地，有 [f(x)dx=[F(x)=F(b)-lim F(x), [f(x)dx=[F(x=lim F(x)-lim F(x)

一、无穷限的反常积分 类似地 有 f (x)dx [F(x) ] lim F(x) lim F(x) x x     = =   . •反常积分的计算 f (x)dx [F(x) ] F(b) lim F(x) x b b   =  =   

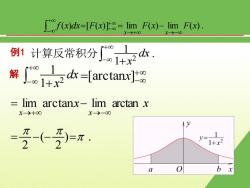
f(dxF(=lim F(x)-lim F(x). X+00 >-00 1计算反常积分∫1京本. 解1+-farctan时 lim arctanx-lim arctan x y=1+x2 a

解 例 1 计算反常积分 dx x2 1 1   . 例 1 f (x)dx [F(x) ] lim F(x) lim F(x) x x   = =   .    =   )= 2 ( 2 . 解      =   [arctan ] 1 1 2 dx x x x x x x lim arctan lim arctan   =  解      =   [arctan ] 1 1 2 dx x x

f(x)dx=[F(x)=lim F(x)-lim F(x). X>+00 X→-00 例2计算反常积分eP'd(p是常数，且p>0) 米jea加-ea 和W1P [cra-l-Twr-gorE =lim [-Lte-pr-1 t-→+0 D2 提示： lim te-p=lim t=lim t>+00 tept 1to Dept

提示： 例 2 计算反常积分 te dt p t  0 (p 是常数 且 p>0). 例2 2 2 2 1 1 ] 1 1 lim [ p p e p te p p t p t t =    =    . 解 2 2 2 1 1 ] 1 1 lim [ p p e p te p pt pt t =    =    . 0 1 lim = lim = lim =     pt t pt t pt t e pe t te 0 . 1 lim = lim = lim =     pt t pt t pt t e pe t te 0 . 1 lim = lim = lim =     pt t pt t pt t e pe t te . f (x)dx [F(x) ] lim F(x) lim F(x) x x     = =   . pt te dt   1 ( ) pt t e dt p  =    1 1 pt pt te e dt p p   =    2 1 1 pt pt te e C p p   =    0 pt te dt   =  2 0 1 1 [ ] pt pt te e p p     

例3时论反常积分2k(@>0)的敛散性 解当p1时，gd==ny。”=to 当p1时，=p=4o0. 当p1时，=-p] lim _1_1apa-p m1-px时1-p=p- 因此，当p>1时，此反常积分收敛，其值P p-T i 当p≤1时，此反常积分发散

解 例 3 讨论反常积分 dx x a p 1   (a>0)的敛散性. 例3 解 当 p=1 时 = =  =     [ln ] 1 1 a a p a dx x x dx x 解 当 p=1 时 = = = .      [ln ] 1 1 a a p a dx x x dx x . 当 p1 时 1 ] 1 1 [ 1 1 1  =  =      p a x p dx x p a p a p . 当p1时 此反常积分发散. 解 当 p=1 时 = =  =     [ln ] 1 1 a a p a dx x x dx x 解 当 p=1 时 = = = .      [ln ] 1 1 a a p a dx x x dx x . 当 p1 时 1 ] 1 1 [ 1 1 1  =  =      p a x p dx x p a p a p 当 p>1 时 . 1 ] 1 1 [ 1 1 1  =  =      p a x p dx x p a p a p . 当 p>1 时 1 ] 1 1 [ 1 1 1  =  =      p a x p dx x p a p a p . 因此 当 p>1 时 此反常积分收敛 其值为 1 1   p a p  1 1 1 1 1 lim 1 1 p p x a p x p    =   

二、无界函数的反常积分 1在0的邻域内无界， X X 称这样的积分为无界函数的反常积分

二、无界函数的反常积分 1 0 1 A dx x =  1 0 x 在 的邻域内无界， 称这样的积分为无界函数的反常积分 1 y x = x y 1