南阳师范学院:《高等数学》课程教学课件(同济第六版)第八章 空间解析几何与向量代数

第一节向量及其线性运算 一、向量概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影
一、向量概念 二、向量的线性运算 四、利用坐标作向量的线性运算 三、空间直角坐标系 五、向量的模、方向角、投影 第一节 向量及其线性运算

一、向量概念 1、概念 (1)向量:既有大小又有方向的量。 如位移、速度、加速度、力、力矩等。,B (2)向量表示:用一条有向线段表示.ū (终点 (3)向量的模向量的大小. A (4)单位向量:模长为1的向量. (起点) (⑤)零向量模长为0的向量,记做0(方向是任意的) (6)自由向量:与起点无关的向量 (7)两向量的夹角: 6 p=位)=6,)0≤ps列 d
⑴向量:既有大小又有方向的量。 如位移、速度、加速度、力、力矩等。 ⑵向量表示:用一条有向线段表示. a 模长为1的向量. 模长为0 的向量,记做0 a || ⑶向量的模:向量的大小. 1、概念 ⑷单位向量: ⑸零向量: 一、向量概念 (6)自由向量:与起点无关的向量 A (起点) B (终点) (方向是任意的) (7)两向量的夹角: a b ba ),( ab ),( 0( )

2、两非零向量的关系 (1)相等:大小相等且方向相同的向量. 记a=b(平行移动后能完全重合) (2)平行:方向相同或相反的两个非零向量.记ā∥ 两向量平行也称为共线 (3)垂直:夹角为元的两个非零向量.记ā1石 注意:由于零向量的方向可以看成任意的,故零 向量与任何向量都平行或垂直。 (4)共面:把若千个向量的起,点放到一起,若它们的 终点和公共起点在同一平面上,则称这些 向量共面
2、两非零向量的关系 ⑴相等:大小相等且方向相同的向量. a b ba 记 ⑵平行:方向相同或相反的两个非零向量. ba 记 // 注意:由于零向量的方向可以看成任意的,故零 向量与任何向量都平行或垂直。 ⑷共面:把若干个向量的起点放到一起,若它们的 终点和公共起点在同一平面上,则称这些 向量共面. (平行移动后能完全重合) 两向量平行也称为共线. ⑶垂直: ba 夹角为 记 的两个非零向量. 2

二、向量的线性运算 1、向量的加减法 (1)加法:a+b=c (平行四边形法则) d (平行四边形法则有时也称为三角形法则) 负向量 (2)减d-b=a+(-时 法: …学d+b c=d+(-b) a-b -a-b
⑵减 法: baba )( a b b b c ba bac )( ba ba a b 1、向量的加减法 ⑴ 加法: cba a b c (平行四边形法则) (平行四边形法则有时也称为三角形法则) 二、向量的线性运算 负向量

2、向量与数的乘法 (1)定义:向量a与实数1的乘积1d是一个新向量. i)2>0,2d与d同向,|2d=2| 2=0,a=0 ii地2<0,2d与d反向,|2i曰2ldl (2)单位向量的表示 向量的单位化 若a40,则有单位向量8- 因此a=lae
2、向量与数的乘法 i ,0) a 与 a 同向, aa |||| ii ,0) 0 a iii ,0) a 与 a 反向, aa |||||| ⑵单位向量的表示 a 0, , a a ea 则有单位向量 因此 . a eaa 若 向量的单位化 ⑴ 定义:向量 与实数 的乘积 a 是一个新向量. a

定理1.设a为非零向量,则a∥b的充分必要条件是 存在唯一的实数入,使b=1d 题以是世)设x-以型 河-40哥-0 故b=d. (“唯一 设又有b=ua,则(2-m)a=0 性”) 而d≠0,故几-4=0,即九=4
定理1. 设a 为非零向量,则 证:(“必要性”) (“唯一 性”) 则 a∥b 设又有b=a , a 0)( a a b a a b 的充分必要条件是 存在唯一的实数,使 设 a∥b , b a 故 b a . b a . 而a 0, 故 0, 即 . ,取 则
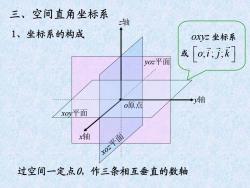
三、空间直角坐标系 z轴 1、坐标系的构成 Oxyz坐标系 或oi,j;k yoz平面 →轴 o原点 xoy平面 x轴 xoz平面 过空间一定点O,作三条相互垂直的数轴
x轴 y轴 z轴 o原点 xoy平面 xoz平面 yoz平面 过空间一定点O,作三条相互垂直的数轴 1、坐标系的构成 三、空间直角坐标系 oxyz 坐标系 或 o i;;;j k

I VI VII 上x 三个坐标平面将空间分成八部分,每一部分叫做一个 卦限
三个坐标平面将空间分成八部分,每一部分叫做一个 卦限

2、向量的坐标表示 在空间直角坐标系下,任意向量下可用向径OM表示. 以i,,分别表示x,y,z轴上的单位向量,设,点M 的坐标为M(x,y,z),则 OM-ON+NM =04+0B+OC d OA=xi,OB=yj,OC=zk k r=xi+yj+zk=(x,y,2) A 此式称为向量下的坐标分解式, xi,yj,z称为向量开沿三个坐标轴方向的分向量
设点 M M x y z ,),,( 则 沿三个坐标轴方向的分向量. kzjyixr x y z),,( x o y z M N B C i j k A 以 ,, kji 分别表示 ,, zyx 轴上的单位向量 , 的坐标为 kzjyix r ,, 称为向量 r 任意向量 可用向径OM 表示. OM N NMO OCOBOA ixOA , jyOB , kzOC 2、向量的坐标表示 在空间直角坐标系下, r 此式称为向量 r 的坐标分解式,

四、利用坐标作向量的线性运算 1、向量的加减法与数乘 a=(ax,a,a,)=ai+ayj+ak; B=(bs,b,B:)=bi+byj+b.k; (1)加法d+b=(a.+b,a,+b,a2+b) =(a+b)i+(a,+b,)j+(a2+b)k; (2)减法d-b=(a-b,a,-b,a:-b) =(a.-b)i+(a,-b,)j+(a2-b)k (3)数乘a=(2ax,2a,a)=(a)i+(n,)j+(a,)k. 2、平行向量的坐标表示式 aWdb=a台(6,b,b)=a,4,0,) (等价→
),,( zyx aaaa ),,( bbbb zyx ⑴加法 ),,( zzyyxx babababa kbajbaiba ;)()()( xx yy zz 1、向量的加减法与数乘 kajaia ; zyx kbjbib ; zyx ),,( babababa zzyyxx kbajbaiba ;)()()( xx yy zz ⑵减法 ),,( aaaa zyx kajaia .)()()( x y z ⑶数乘 2、平行向量的坐标表示式 abba // ),,(),,( zyx aaabbb zyx z z y y x x a b a b a b 四、利用坐标作向量的线性运算 (等价)
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第六章 定积分在几何中的应用.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第二章 导数与微分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第一章 函数与极限.pdf
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)第十章 无穷级数.pdf
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)第八章 重积分.pdf
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)第七章 向量代数与空间解析几何.pdf
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)第六章 向量代数与空间解析几何.pdf
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)第五章 定积分.pdf
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)第四章 不定积分.pdf
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)第三章 中值定理与导数的应用.pdf
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)第二章 导数与微分.pdf
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)数字特征习题.doc
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)概率统计——二维随机变量及其分布.doc
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)第一章 函数与极限.pdf
- 南阳师范学院:《高等数学》课程教学资源(试卷习题)第七章 向量代数与空间解析几何.pdf
- 《现代数值分析》课程参考资料(数值线性代数)Predictions for scientific computing 50 years from now,L.N. Trefethen, Mathematics Today, 2000.pdf
- 华东师范大学:《现代数值分析》课程教学课件(数值线性代数)第六讲 线性方程组基本迭代解法.pdf
- 华东师范大学:《现代数值分析》课程教学课件(数值线性代数)第五讲 对称矩阵的特征值问题(5.4-5.7).pdf
- 华东师范大学:《现代数值分析》课程教学课件(数值线性代数)第五讲 对称矩阵的特征值问题(5.1-5.3).pdf
- 《现代数值分析》课程参考资料(数值线性代数)Francis's Algorithm(Watkins, American Mathematical Monthly, 2011).pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第九章 多元函数微分法及其应用.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十章 重积分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第三章 微分中值定理与导数的应用 3.1 微分中值定理.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第三章 微分中值定理与导数的应用 3.2 洛必达法则.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第三章 微分中值定理与导数的应用 3.3 泰勒公式.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第三章 微分中值定理与导数的应用 3.4 函数的单调性与凸凹性.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第三章 微分中值定理与导数的应用 3.5 函数的极值与最大值最小值.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第三章 微分中值定理与导数的应用 3.6 函数图形的描绘.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第三章 微分中值定理与导数的应用 3.7 曲率.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第五章 定积分及其应用 5.1 定积分的概念与性质.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第五章 定积分及其应用 5.2 微积分基本公式.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第五章 定积分及其应用 5.3 定积分的换元法及分部积分法.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第五章 定积分及其应用 5.4 反常积分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.1 对弧长的曲线积分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.2 对坐标的曲线积分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.3 格林公式及其应用.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.4 对面积的曲面积分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.5 对坐标的曲面积分.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.6 高斯公式.pdf
- 南阳师范学院:《高等数学》课程教学课件(同济第六版)第十一章 曲线积分与曲面积分 11.7 斯托克斯公式.pdf
