南阳师范学院：《高等数学》课程教学课件（同济第六版）第九章 多元函数微分法及其应用

第九章多元函数微分法及其应用 一元函数微分学 推广 多元函数微分学

推广 第九章 一元函数微分学 多元函数微分学 多元函数微分法及其应用

第一节 多元函数的基本概念 一、区域 二、多元函数的概念 三、多元函数的极限 四、多元函数的连续性

第一节 一、区域 二、多元函数的概念 三、多元函数的极限 四、多元函数的连续性 多元函数的基本概念

一、区域 1.邻域 点集U(,δ)={PPP<6},称为点Po的6邻域. 例如，在平面上， U(,δ)={《x,y)V(x-x2+(y-%)2<6}(圆邻域) 在空间中， U(D,6)={(xy,zV(x-x)2+(y-%)2+(z-0)2<6} (球邻域) 说明：若不需要强调邻域半径6，也可写成U() 点Po的去心邻域记为U(P)={P0<PP<δ}

0 )(   o  PPU  PP  δ 0 0 一、 区域 1. 邻域 点集  , ),(PU 0 δ  P 称为点 P0 的 邻域. 例如,在平面上, PU 0 δ   yx ),(),(  (圆邻域) 在空间中, 0    zyxPU ),,(),(  (球邻域) 说明：若不需要强调邻域半径 ,也可写成 .)( U P0 点 P0 的去心邻域记为 PP  δ 0 yyxx  δ 2 0 2 0 )()( zzyyxx  δ 2 0 2 0 2 0 )()()(

2.区域 (1)内点、外点、边界点 设有点集E及一点P: ·若存在点P的某邻域U(P)cE, 则称P为E的内点； ·若存在点P的某邻域U(P)∩E=☑， 则称P为E的外点； ·若对点P的任一邻域UP)既含E中的内点也含E 的外点，则称P为E的边界点 显然，E的内点必属于EE的外点必不属于E,E的 边界，点可能属于E,也可能不属于E

2. 区域 (1) 内点、外点、边界点 设有点集 E 及一点 P :  若存在点 P 的某邻域 U(P) E ,  若存在点 P 的某邻域 U(P)∩ E =  ,  若对点 P 的任一邻域 U(P) 既含 E中的内点也含 E E 则称 P 为 E 的内点； 则称 P 为 E 的外点 ; 则称 P 为 E 的边界点 的外点 , . 显然, E 的内点必属于 E , E 的外点必不属于 E , E 的 边界点可能属于 E, 也可能不属于 E . P

(2)聚点 若对任意给定的δ，点P的去心 E 邻域U(P,δ)内总有E中的点，则 称P是E的聚点 聚点可以属于E,也可以不属于E(因为聚点可以为 E的边界，点)

(2) 聚点 若对任意给定的 ,点P 的去心 (PU δ),  E 邻域 内总有E 中的点 , 则 称 P 是 E 的聚点. 聚点可以属于 E , 也可以不属于 E (因为聚点可以为 E 的边界点 )

(③)开区域及闭区域 。若点集E的点都是内点，则称E为开集； ·E的边界点的全体称为E的边界，记作OE, ·若，点集E一OE,则称E为闭集； ·若集D中任意两，点都可用一完全属于D的折线相连 则称D是连通的； ·连通的开集称为开区域，简称区域； ·开区域连同它的边界一起称为闭区域

D (3) 开区域及闭区域  若点集 E 的点都是内点，则称 E 为开集；  若点集 E E , 则称 E 为闭集；  若集 D 中任意两点都可用一完全属于 D 的折线相连 ,  开区域连同它的边界一起称为闭区域. 则称 D 是连通的 ;  连通的开集称为开区域 ,简称区域 ; 。 。  E 的边界点的全体称为 E 的边界, 记作E ;

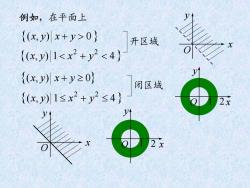
例如，在平面上 {(x)x+y>0} 开区域 {(x,y)1<x2+y2<4} {x,y)x+y≥0} 闭区域 {(x,y)1≤x2+y2≤4} 2x

例如，在平面上  yxyx  0),(   1),( 4  22 yxyx   yxyx  0),(   1),( 4  22 yxyx  开区域 闭区域 x y O x y O 1 2 x y O x y O 1 2

整个平面是最大的开域， 也是最大的闭域， 点集{(x,y)川x>1}是开集， 但非区域 对区域D,若存在正数K,使一切点PD与某定点 A的距离APkK,则称D为有界域，否则称为无 界域

整个平面 点集 xyx 1),( 是开集， 是最大的开域 , 也是最大的闭域 ; 但非区域 . 1 1 对区域 D , 若存在正数 K , 使一切点 PD 与某定点 A 的距离 AP K , 则称 D 为有界域 , 界域 . 否则称为无 x y O

二、多元函数的概念 定义1.设非空点集DCR”,映射f:D→R称为定义 在D上的n元函数，记作 u=f(x1,x2,…,xn)或u=f(P),P∈D 点集D称为函数的定义域；数集{uu=f(P),P∈D} 称为函数的值域。 特别地，当n=2时，有二元函数 z=f(x,y),(x,y)∈DcR2 当n=3时，有三元函数 u=f(x,y,z), (xy,z)∈DcR3

定义1. 设非空点集 , n D  R 或  ,)(  DPPfu 点集 D 称为函数的定义域 ; 数集  )(  DP,Pfuu  称为函数的值域 . 特别地 , 当 n = 2 时, 有二元函数 2  ),(),,( Dyxyxfz  R 当 n = 3 时, 有三元函数 3  ),,(),,,( Dzyxzyxfu  R 映射 f : D  R称为定义 在 D 上的 n 元函数 , 记作 ),,,( 21 n u  f  xxx 二、多元函数的概念

三、多元函数的极限 定义2.设n元函数f(P),P∈DcR”,Po是D的聚 点，若存在常数A,对任意正数ε，总存在正数6，对一 切P∈D∩U(P,),都有f(P)-A<c,则称A为函数 f(P)当PP时的极限，记作 lim f(P)=A(也称为n重极限) P→0 当n-2时，记p=PR=V(x-xo)2+(y-yo)2 二元函数的极限可写 作：limf(x,y)=A=limf(x,)=A p→0 x→x0 y→yo

三、多元函数的极限 定义2. 设 n 元函数 ( , n ), DPPf  R 点 , ,),( 0PUDP δ     APf  ε,)( 则称 A 为函数 (也称为 n 重极限 ) 当 n =2 时, 记 2 0 2 0 0   yyxxPP )()( 二元函数的极限可写 作： f  Ayx  ),(lim 0 f P A PP   )(lim0 P0 是 D 的聚 若存在常数 A , 对一 )( 当  PPPf 0时的极限，记作 f Ayx yy xx     ),(lim 0 0 都有 对任意正数  , 总存在正数  , 切