《信号与系统》课程教学课件（PPT讲稿）§8.1 引言

③号与兼安 §8.1引言 ￥ 新疆大学信息科学与工程学院电子系 2003.1 退出 开始

新疆大学信息科学与工程学院电子系 2003.1 §8.1 引言

引言 求解差分方程的工具，类似于拉普拉斯变换； z变换的历史可是追溯到18世纪； 20世纪50~60年代抽样数据控制系统和数字计算机的 研究和实践，推动了变换的发展； 70年代引入大学课程： 今后主要应用于DSP分析与设计，如语音信号处理等 问题。 本章主要讨论： 拉氏变换的定义、收敛域、性质，与傅氏变换和拉氏 变换的关系；利用z变换解差分方程； 利用z平面零极点的分布研究系统的特性。 合UD

X 第 2 页 •求解差分方程的工具，类似于拉普拉斯变换； •z变换的历史可是追溯到18世纪； •20世纪50~60年代抽样数据控制系统和数字计算机的 研究和实践，推动了z变换的发展； •70年代引入大学课程； •今后主要应用于DSP分析与设计，如语音信号处理等 问题。 本章主要讨论： •拉氏变换的定义、收敛域、性质，与傅氏变换和拉氏 变换的关系；利用z变换解差分方程； •利用z平面零极点的分布研究系统的特性。 一．引言

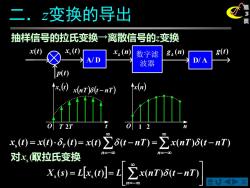
二.z变换的导出 抽样信号的拉氏变换→离散信号的z变换 x(t) x,(t) xk (n) 数字滤 8k(n) 8(t) A/D 波器 D/A ↑x(d) x(nT)5t-nT） x(n) 0T27 x@=r0-d,(④=x0∑6t-mn)=∑xnn)8t-nI) 对x,取拉氏变换 X,=c-L∑T)e-n)

X 第 3 二． 页 z变换的导出 抽样信号的拉氏变换→离散信号的z变换 ( ) ( ) ( ) s x t x t t  T =     =−   =−  = − = − n n x(t)  (t nT) x(nT) (t nT) 对 ( 取拉氏变换 ) s x t         = =  −  n=−  X (s) L x (t) L x(nT) (t nT) s s  ( ) s x t A/ D x (n) k 数字滤 波器 g (n) k D/ A g(t) p(t) x(t) O t x (t) s T 2T x(nT) (t − nT) O n x(n) 1 2

x,)=∑x(nT)Z[5t-nT]=∑x(nTe 其中s=g+j0 引入复变量z=er,为连续变量，将x(nT表示为r(n) X,(l,=∑x(mz"=Xa) 1=-0 对任一信号(n)的（双边）z变换式为 X(a)=∑x(nmz

X第4页 ( )     =−  =−  − = − = n n snT X s x(nT)L (t nT) x(nT)e s  其中 s = σ + j ω 引入复变量 z = e sT， 为连续变量 ( ) | ( ) ( ) s e X s x n z X z n n z s T =  = =−  − = 对任一信号x(n)的（双边） z变换式为 =−  − = n n X ( z ) x ( n ) z ，将x (nT )表示为x (n )

三.对z变换式的理解 00 Xa)=Σx(z” 1=-0∞ =.x(-2)z2+x(-1)z1 的正幂 +x(0)z°+x(1)z1+x(2)z2+.x(n)z”+ 的负幂 X2)是z的幂级数 级数的系数是x(n) 幂-n中的n指出x(n)的位置

X 第 5 页   =−  − = n n X(z) x(n)z      的负幂 的正幂 z n z x z x z x z x n z x z x z + + + + + = − + − − − − (0) (1) (2) ( ) ( 2) ( 1) 0 1 2 2 1 X(z)是z −1 的幂级数 幂− n中的n指出 x(n) 的位置 级数的系数是 x(n) 三．对z变换式的理解

说明 -o<n≤-1 z的正幂级数构成左边列 0≤n<oo z的负幂级数构成右边列 ●若双边序列取单边变换，或对因果信号（有起因序 列)n≥府在的序列取变换 Xa)=∑x(n)z"， 单边z变换 n=0

X 第 6 说明 页 X z x n z 单 边z变 换 n n ( ) ( ) , 0   = − = 0  n   z的负幂级数构成右边序列 −   n  −1 z的正幂级数构成左边序列 若双边序列取单边z变换，或对因果信号（有起因序 列） n  存在的序列取 0 z变换