《信号与系统》课程教学课件（PPT讲稿）§7.3 离散时间系统的数学模型—差分方程

心号与乘突 § 73离款时间系统的数学 模型一差分方程 ·用差分方程描述线性时不变离散系统 由实际问题直接得到差分方程 由微分方程导出差分方程 由系统框图写差分方程 ,差分方程的特点 新疆大学信息科学与工程学院电子系 2003.1 退出 开始

新疆大学信息科学与工程学院电子系 2003.1 §7.3 离散时间系统的数学 模型—差分方程 •用差分方程描述线性时不变离散系统 •由实际问题直接得到差分方程 •由微分方程导出差分方程 •由系统框图写差分方程 •差分方程的特点

用差分方程描述线性时不变离散裂绕 线性：均匀性、可加性均成立： x,(n) y(n 离散时间系统 x2(n) 离散时间系统 r2(n) c1x1(n)+c2x2(n) ciy(n)+c2y2(n) 离散时间系统

X 第 2 一．用差分方程描述线性时不变离散系统页 离散时间系统 ( ) x1 n ( ) y1 n 离散时间系统 ( ) x2 n ( ) y2 n 离散时间系统 ( ) ( ) c1 x1 n + c2 x2 n ( ) ( ) c1 y1 n + c2 y2 n 线性：均匀性、可加性均成立；

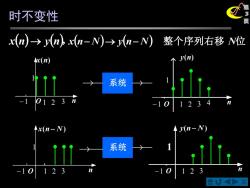
时不变性 x(m)→(nx(a-N)→(a-N） 整个序列右移N位 x(n) y(n 系统 0123 -10 123 n-N y(n-N 系统 1 -1 123 1

X 第 3 时不变性 页 x(n) → y(n)，x(n− N)→ y(n− N) 整个序列右移 N位 O n x(n) 1 −1 1 2 3 系统 O n y(n) 1 −1 1 2 3 4 O n x(n − N ) 1 −1 1 2 3 系统 O n y(n − N ) 1 −1 1 2 3

二，由实际问题直接得到差分方程 例如： Jy(n)表示一个国家在第n年的人口数 (常数)：出生率 b(常数)：死亡率 设x(n)是国外移民的净增数 则该国在第+1年的人口总数为： J(+1)-y(n+y(n)-by(n)+x(n） =(a-b+1)y(n)+x(n)

X 第 4 二．由实际问题直接得到差分方程 页 例如： y(n)表示一个国家在第n年的人口数 a(常数)：出生率 b(常数): 死亡率 设x(n)是国外移民的净增数 则该国在第n+1年的人口总数为： y(n+1)=y(n)+ay(n)-by(n)+x(n) =(a-b+1)y(n)+x(n)

三.由微分方程导出差分方程 0=0+f0 dt yG) 输出 ft)输入 时间间隔：T 后差 ⑨0)-t-T） dt 或前差 ≈t+T小- dt

X 第 5 三．由微分方程导出差分方程 页 ( ) ( ) ( ) T y t y t T t y t − −  d d ( ) ( ) ( ) T y t T y t t y t + −  d d 后差 或前差 ( ) ay(t) f (t) t y t = + d d y(t)：输出 f (t)：输入 时间间隔 : T

列差分方程 若用后差形式 -T）=o0+0) T 若在仁nT各点取得样值 d)=nr)→(a n代表序号 fd)=f(nT）-→fn -=+m =-*a网 当前输出 前一个输出 输入 合UD

X 第 6 列差分方程 页 y(t) = y(nT) → y(n) f (t) = f (nT)→ f (n) ( ) ( ) ay(n) f (n) T y n y n = + − −1 ( ) ( ) f (n) aT T y n aT y n − − + − = 1 1 1 1 若用后差形式 ( ) ( ) ay(t) f (t) T y t y t T = + − − 若在t=nT 各点取得样值 当前输出 前一个输出 输入 n代表序号

四.由系统框图写差分方程 1.基本单元 加法器： x(n) x (n)+x2(n) x,(n) ,( 乘法器 x(n） x (n)-x,(n) x2(n) 合U>风

X 第 7 四．由系统框图写差分方程 页 1．基本单元 x (n) 1 x (n) 2 x (n) x (n) 1 + 2  x (n) 1 x (n) 2 x (n) x (n) 1 + 2 加法器： 乘法器： x (n) 1 x (n) 2 x (n) x (n) 1 2 

系统框图 标量乘法器 x(n) ax(n) x(n)a ax(n) 延时器 2） y(n-1) 单位延时实际是一个移位寄存器，把前一个离 散值顶出来，递补。 创题 合U少通

X 第 8 页 x(n) ax(n) a x(n) a ax(n) 延时器 单位延时实际是一个移位寄存器，把前一个离 散值顶出来，递补。 y(n) y(n −1) E 1 y(n) y(n −1) −1 z 标量乘法器 系统框图

五.差分方程的特点 (1)输出序列的第个值不仅决定于同一瞬间的输入样 值，而且还与前面输出值有关，每个输出值必须依次 保留。 (2)差分方程的阶数：差分方程中变量的最高和最低 序号差数为阶数。 如果一个系统的第个输出决定于刚过去的几个输出 值及输入值，那么描述它的差分方程就是几阶的。 通式立a-)-立，x-）

X 第 9 五．差分方程的特点 页 (1)输出序列的第n个值不仅决定于同一瞬间的输入样 值，而且还与前面输出值有关，每个输出值必须依次 保留。 (2)差分方程的阶数：差分方程中变量的最高和最低 序号差数为阶数。 如果一个系统的第n个输出决定于刚过去的几个输出 值及输入值，那么描述它的差分方程就是几阶的。  ( )  ( ) = = − = − M r r N k k a y n k b x n r 0 0 通 式:

差分方程的特点 (3)微分方程可以用差分方程来逼近，微分方程解是 精确解，差分方程解是近似解，两者有许多类似之 处。 (4)差分方程描述离散时间系统，输入序列与输出序 列间的运算关系与系统框图有对应关系，应该会写会 画

X 第 10 差分方程的特点 页 (4)差分方程描述离散时间系统，输入序列与输出序 列间的运算关系与系统框图有对应关系，应该会写会 画。 (3)微分方程可以用差分方程来逼近，微分方程解是 精确解，差分方程解是近似解，两者有许多类似之 处