《信号与系统》课程教学课件(PPT讲稿)§5.9 从抽样信号恢复连续时间信号

心号与事我 §5,9从抽样信号恢复 连续时间信号 由抽样信号恢复原信号 零阶抽样保持 头 新疆大学信息科学与工程学院电子系 2003.1 退出 开始
新疆大学信息科学与工程学院电子系 2003.1 § 5.9 从抽样信号恢复 连续时间信号 •由抽样信号恢复原信号 •零阶抽样保持

由抽样信号恢复原信号 理想低通滤波器 个Fs(o) 0s>20 H0)- w>o. O0m F(@)=F(@)H(o)fd)=fd)*t) 滤除高频成分,即可恢复原信号 -0c00c F@ 从时域运算解释 -000m 0 合U
X 第 2 页 理想低通滤波器 滤除高频成分,即可恢复原信号 ( ) = c s c 0 T H F( ) = F ( ) H( ) f (t) = f (t)h(t) s s 一.由抽样信号恢复原信号 o H() − C C TS o F() − m m 1 o () FS S 1 T −S m S S − m S 2 m 从时域运算解释

时域运算 以理想抽样为例 时域:f)=f)6,(0)=∑f(nT)5t-nT) 1=-c0 缬域:Fo)=2 F)-P(w=)2ro-na) 理想低通滤波器 o>0 时球:h0=r2so,动 0=a-28-:gs®,) =T9∑fnI)sa@.i-nr)】 元
X 第 3 时域运算 页 以理想抽样为例 =− = = − n f (t) f (t) (t) f (nT ) (t nT ) 时域: s T s s ( ) ( ) ( ) ( ) =− = = − n F n T F F P s S s 1 2π 1 频域: 理想低通滤波器: ( ) = c s c 0 T 频域:H h(t) T ( t) c c s Sa π 时域: = ( ) ( ) ( ) = = − =− f t f t h t f nT t nT T t n c c s s s s Sa π ( ) ( ) ( ) ( ) s c s c s ( )Sa π T f nT t nT n = − =−

说明 r()=nruT)salo.(-nT)] =-00 连续信号f)可以展开成Sa函数的无穷级数,级数的系 数等于抽样值fnTs)。 ·也可以说在抽样信号f①)的每个抽样值上画一个峰值 为fnT)的Sa函数波形,由此合成的信号就是)。 当0,=20m’则有0.=0m,T、= 2π 元 此时r0)=ΣfnI)sa[o.k-mI)] 演示
X 第 4 页 • 连续信号f(t)可以展开成Sa函数的无穷级数,级数的系 数等于抽样值f(nTs )。 • 也可以说在抽样信号fs (t)的每个抽样值上画一个峰值 为f(nTs ) 的Sa函数波形,由此合成的信号就是fs (t) 。 s c m c m s 2π π 2 , 当s = ,则有 = T = = ( ) ( ) s Sa c s f t f (nT ) t nT n = − =− 此 时 ( ) ( ) s c s c s ( )Sa π f t T f nT t nT n = − =− 说明
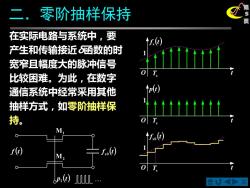
二.零阶抽样保持 在实际电路与系统中,要 产生和传输接近6涵数的时 宽窄且幅度大的脉冲信号 比较困难。为此,在数字 通信系统中经常采用其他 ↑pd 抽样方式,如零阶抽样保 tttttttt 持。 r(t M
X 第 5 二.零阶抽样保持 页 M1 M2 f (t) f (t) s0 p (t) 1 在实际电路与系统中,要 产生和传输接近δ函数的时 宽窄且幅度大的脉冲信号 比较困难。为此,在数字 通信系统中经常采用其他 抽样方式,如零阶抽样保 持。 O f (t) s t 1 O f (t) s0 t 1 Ts Ts O p(t) t 1 Ts

ho(t) 为求得断d)的频谱,构造一个线姓时不变系统 n( 积分器 五) n()=[[5()-5(-T.)at=u()-u(-7.) n.-tsa To
X第6页 h 0 ( t) 为求得fs0 (t)的频谱,构造一个线性时不变系统: 积分器 Ts f (t) s + − f (t) s0 h (t) 0 ( ) ( ) ( ) ( ) ( ) 0 s d Ts h t t t T t u t u t t = − − = − − − ( ) 2 j s 0 s s 2 Sa T e T H T − =
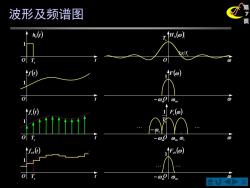
波形及频谱图 ↑,(d TfH.(o) o T. r -000m F.) @O 0m0 0 n.() fF.(@) O T. -000m
X 第 7 波形及频谱图 页 O h (t) 0 t 1 Ts O O f (t) t 1 O f (t) s t 1 O f (t) s0 t 1 Ts () H0 π s 2 T O F() − m m O () Fs − m m −s s 1 s 1 T O () Fs0 − m m 1 Ts Ts

补偿低通滤波器 F,(o)=F,(o)H(o) [2e-〉] -a)so 补偿低通滤波器 Sa 合U
X 第 8 补偿低通滤波器 页 ( ) ( ) ( ) ( ) ( ) =− − − =− = − = − = n T T n s s T F n T F n T T F F H 2 j s 2 j s s s s 0 0 s s s e 2 Sa e 2 Sa 1 补偿低通滤波器 = 2 0 2 e 2 Sa 1 s s 2 j s 0r s T T H

信号的恢复 F.@) 补偿低通滤波器 Sa -0.0m Hor(j@) p@ 0 0> @.0 此滤波器的相位超前, 无法实现,实际中允许 F(o】 延时存在,但要求系统 为线性相位。 -0.01 合心D风
X 第 9 信号的恢复 页 O (j) H0r 2 s − 2 s O () 2 s − 2 s O () Fs0 − m m 1 O F() − m m 1 补偿低通滤波器 = 2 0 2 e 2 Sa 1 s s 2 j s 0r s T T H 此滤波器的相位超前, 无法实现,实际中允许 延时存在,但要求系统 为线性相位
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《信号与系统》课程教学课件(PPT讲稿)§5.8 带通滤波系统的运用.ppt
- 《信号与系统》课程教学课件(PPT讲稿)辐射与波长的关系.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§5.7 调制与解调.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§5.6 希尔伯特变换.ppt
- 《信号与系统》课程教学课件(PPT讲稿)可实现的低通.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§5.5 系统的物理可实现性、佩利-维纳准则.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§5.4 理想低通滤波器.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§5.3 无失真传输.ppt
- 《信号与系统》课程教学课件(PPT讲稿)正弦信号激励下系统的稳态响应.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§5.2 利用系统函数求响应.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§5.1 引言.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§4.12 拉普拉斯变换与傅氏变换的关系.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§4.9 全通函数与最小相移函数的零、极点分布.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§4.11 双边拉氏变换.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§4.10 线性系统的稳定性.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§4.8 由系统函数零、极点分布决定频响特性.ppt
- 《信号与系统》课程教学课件(PPT讲稿)比较H(s)和H(p).ppt
- 《信号与系统》课程教学课件(PPT讲稿)§4.7系统函数零、极点分布决定时域特性.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§4.6 系统函数(网络函数)H(S).ppt
- 《信号与系统》课程教学课件(PPT讲稿)§4.5 用拉普拉斯变换法分析电路、S域元件模型.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§5.10 脉冲编码调制(PCM).ppt
- 《信号与系统》课程教学课件(PPT讲稿)§5.11 频分复用与时分复用.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§6.1 引言.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§6.2 信号矢量空间的基本概念.ppt
- 《信号与系统》课程教学课件(PPT讲稿)柯西-施瓦茨不等式.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§6.3 信号的正交函数分解.ppt
- 《信号与系统》课程教学课件(PPT讲稿)相关系数.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§6.4 完备正交函数集、帕塞瓦尔定理1.ppt
- 《信号与系统》课程教学课件(PPT讲稿)帕塞瓦尔定理证明.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§6.5 相关.ppt
- 《信号与系统》课程教学课件(PPT讲稿)相关定理证明.ppt
- 《信号与系统》课程教学课件(PPT讲稿)相关系数.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§6.6 能量谱和功率谱.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§6.7 信号通过线性系统的自相关函数能量谱和功率谱分析.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§6.8 匹配滤波器.ppt
- 《信号与系统》课程教学课件(PPT讲稿)匹配滤波器的约束关系.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§6.9 码分复用、码分多址(CDMA)通信.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§7.1 引言.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§7.2 离散时间信号——序列.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§7.3 离散时间系统的数学模型—差分方程.ppt
