《高等数学》课程教学课件（讲稿）余弦函数的图像与性质

数学（二） 第四章：三角函数

三角函数 数学（二） 第四章：三角函数

第九讲 余弦函数的图像与性质 主讲人：黄发英

三角函数 第九讲： 余弦函数的图像与性质 主讲人：黄发英

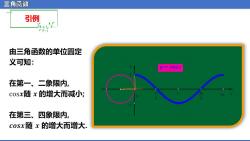
三角还数 引例 由三角函数的单位圆定 义可知： M三C0a 在第一、二象限内， cosx随x的增大而减小； 在第三、四象限内， cosx随x的增大而增大

三角函数 引例

三角函数 我们用描点法作出了正弦函数y=six在[0,2π]上的图像，通过不断 向左、向右平移（每次移动2π个单位长度）得到了正弦函数 y=sinx,x∈R的图像，并通过正弦曲线研究了正弦函数的性质. 对于余弦函数y=cosx,x∈R,可否用同样的方法来研究？ y=cosa (cosa sina) 0 -2m 2m 3π 4m x

三角函数

三角还数 举例 例1用描点法作出余弦函数y=coSx在[0,2π]上的图像！ (1)列表 把区间0,2π]分成12等份，分别求出y=cosx在各分点及区 间端点的余弦函数值. π 几-3 2π 5π 7x 4π 3π 5π 0 11π 2 6 2π 6 3 6 3 2 3 6 5 3 5 y=cOSx 0 -1 0 2 2 2 2 2 2 2 2

三角函数 举例

三角函数 (2)描点作图 . 根据表中x,y的数值在平面直角坐标系内描点(x,y),再用 平滑曲线顺次连接各点，就得到余弦函数y=cosx在[O,2π]上的 图像. y=c0sE,x∈0,2π] 0 π 5T 74r35m11T2x 3 3236

三角函数 (2) 描点作图．

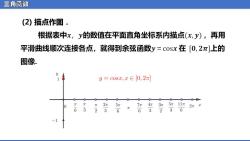
三角函数 (2)描点作图 根据表中x,y的数值在平面直角坐标系内描点(x,y)，再用 平滑曲线顺次连接各点，就得到余弦函数y=Cosx在[0,2π]上的 图像。 9 y=c0sx,x∈0,2π 0 Tππ2π 7π4r3r 5m11T2元x 6323 6 63236

三角函数 (2) 描点作图．

三角函数 观察函数y=c0Sx在[0,2π上的图像发现，在确定图像的 形状时，起关键作用的点有以下五个，描出这五个点后，余弦 函数的图像就基本确定了. (0,1), y=c0sx,x∈[0,2π] 3n 2 2 2

三角函数

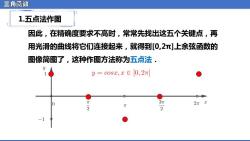
三角函数 1.五点法作图 因此，在精确度要求不高时，常常先找出这五个关键点，再 用光滑的曲线将它们连接起来，就得到[0,2π]上余弦函数的 图像简图了，这种作图方法称为五点法. y=c0sx,x∈0,2r] 0 3不 2πx 2 2

三角函数 1.五点法作图 因此，在精确度要求不高时，常常先找出这五个关键点，再 用光滑的曲线将它们连接起来，就得到[0,2π]上余弦函数的 图像简图了，这种作图方法称为五点法．

三角函数 因为余弦函数的周期是2π，所以余弦函数值每隔2π重 复出现一次.于是，我们只要将函数y=cosx在[0,2π上的 图像沿x轴向左或向右平移2kπ(k∈Z),就可得到余弦函数 y=coSx,x∈R的图像余弦函数的图像也称为余弦曲线， 它是一条“波浪起伏”的连续光滑曲线. -2 2元 4元

三角函数 ᵆ ᵆ ᵄ 2ᵰ 4ᵰ