聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 2.6 基与于基

第六节基与于基

定义2.6.1设(X,T)是一个拓扑空 间,B是T的一个子族.如果T中的 每一个元素(即拓扑空间X中的每一个 开集)是B中某些元素的并,即对于每 一个U∈T,存在B,cB使得 U=UB B∈B1 则称B是拓扑T的一个基,或称B是 拓扑空间X的一个基
B B 1 B B 1 U B = 定义2.6.1 设(X, T)是一个拓扑空 间,B 是 T 的一个子族.如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并,即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基,或称B 是 拓扑空间 X 的一个基. B B 1 B B 1 U B = 定义2.6.1 设(X, T)是一个拓扑空 间,B 是 T 的一个子族.如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并,即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基,或称B 是 拓扑空间 X 的一个基. B B 1 B B 1 U B = 定义2.6.1 设(X, T)是一个拓扑空 间,B 是 T 的一个子族.如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并,即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基,或称B 是 拓扑空间 X 的一个基. B B 1 B B 1 U B = 定义2.6.1 设(X, T)是一个拓扑空 间,B 是 T 的一个子族.如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并,即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基,或称B 是 拓扑空间 X 的一个基. B B 1 B B 1 U B = 定义2.6.1 设(X, T)是一个拓扑空 间,B 是 T 的一个子族.如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并,即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基,或称B 是 拓扑空间 X 的一个基. B B 1 B B 1 U B = 定义2.6.1 设(X, T)是一个拓扑空 间,B 是 T 的一个子族.如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并,即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基,或称B 是 拓扑空间 X 的一个基. B B 1 B B 1 U B = 定义2.6.1 设(X, T)是一个拓扑空 间,B 是 T 的一个子族.如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并,即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基,或称B 是 拓扑空间 X 的一个基. B B 1 B B 1 U B = 定义2.6.1 设(X, T)是一个拓扑空 间,B 是 T 的一个子族.如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并,即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基,或称B 是 拓扑空间 X 的一个基. B B 1 B B 1 U B = 定义2.6.1 设(X, T)是一个拓扑空 间,B 是 T 的一个子族.如果 T 中的 每一个元素(即拓扑空间 X 中的每一个 开集)是 B 中某些元素的并,即对于每 一个 U∈T ,存在 使得 则称 B 是拓扑T 的一个基,或称B 是 拓扑空间 X 的一个基.

定理2.6.1一个度量空间中的 所有球形邻域构成的集族是这个度 量空间作为拓扑空间时的一个基. 注:(1)实数空间R中所有的开区间 构成的集族是它的一个基。 (2)离散空间中所有单点集构成 的族是它的一个基
定理2.6.1 一个度量空间中的 所有球形邻域构成的集族是这个度 量空间作为拓扑空间时的一个基. 注:(1)实数空间 R 中所有的开区间 构成的集族是它的一个基. (2)离散空间中所有单点集构成 的族是它的一个基

问 题 ◆任何一个拓空间是否都存在基? ◆拓扑空间的基是否夺一?
问 题 ◆任何一个拓扑空间是否都存在基? ◆拓扑空间的基是否存一?

定理2.6.2 设B是拓扑空间 (X,T)的一个开集族,则B是拓扑 空间X的一个基当且仅当对于每一 个x∈X和x的每一个邻域U, 存在V∈B使得x∈VCU
Ux Vx B x x x V U 定 理2.6.2 设 B 是拓扑空间 (X,T)的一个开集族,则 B 是拓扑 空间 X 的一个基当且仅当对于每一 个 x∈X 和 x 的每一个邻域 , 存在 使得 . Ux Vx B x x x V U 定 理2.6.2 设 B 是拓扑空间 (X,T)的一个开集族,则 B 是拓扑 空间 X 的一个基当且仅当对于每一 个 x∈X 和 x 的每一个邻域 , 存在 使得 . Ux Vx B x x x V U 定 理2.6.2 设 B 是拓扑空间 (X,T)的一个开集族,则 B 是拓扑 空间 X 的一个基当且仅当对于每一 个 x∈X 和 x 的每一个邻域 , 存在 使得 . Ux Vx B x x x V U 定理2.6.2 设 B 是拓扑空间 (X,T)的一个开集族,则 B 是拓扑 空间 X 的一个基当且仅当对于每一 个 x∈X 和 x 的每一个邻域 , 存在 使得

证明:必要性:如果B是X的 一个基,则对于每一个x∈X和x的 每一个邻域U,存在x的一个开邻 域W,使得x∈WcUx.由于W 是一个开集,根据基的定义,存在 B,cB,使得W=UA.故存在 A∈B1 V,∈B,cB使得 x∈VCUA=W,cU, A∈B1
证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U = 证明:必要性:如果 B 是 X 的 一个基,则对于每一个 x∈X 和 x 的 每一个邻域 ,存在 x 的一个开邻 域 使得 .由于 是—个开集,根据基的定义,存在 ,使得 .故存在 使得 Ux Wx x x x W U Wx B B 1 B 1 x A W A = Vx B B 1 B 1 x x x A x V A W U =
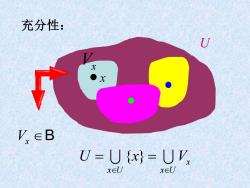
充分性: U X ●x y∈B U=Ux=UK x∈UJ x∈LU
充分性: U x Vx Vx B { } x x U x U U x V = =

充分性:如果是X中的任意开 集,则对于每一个x∈U,由于U是x 的一个邻域,故存在V∈B,使得 x∈VcU.于是 U=UxEUK.cU x∈UU x∈LU 因此U=UV,,故U是B中某些 XEU 元素之并,从而B是X的一个基
充分性:如果 U 是 X 中的任意开 集,则对于每一个 x∈U,由于U 是 x 的一个邻域,故存在 ,使得 . 于是 因此 ,故 U 是 B 中某些 元素之并,从而 B 是 X 的一个基. x x V U Vx B { } x x U x U U x V U = x x U U V = 充分性:如果 U 是 X 中的任意开 集,则对于每一个 x∈U,由于U 是 x 的一个邻域,故存在 ,使得 . 于是 因此 ,故 U 是 B 中某些 元素之并,从而 B 是 X 的一个基. x x V U Vx B { } x x U x U U x V U = x x U U V = 充分性:如果 U 是 X 中的任意开 集,则对于每一个 x∈U,由于U 是 x 的一个邻域,故存在 ,使得 . 于是 因此 ,故 U 是 B 中某些 元素之并,从而 B 是 X 的一个基. x x V U Vx B { } x x U x U U x V U = x x U U V = 充分性:如果 U 是 X 中的任意开 集,则对于每一个 x∈U,由于U 是 x 的一个邻域,故存在 ,使得 . 于是 因此 ,故 U 是 B 中某些 元素之并,从而 B 是 X 的一个基. x x V U Vx B { } x x U x U U x V U = x x U U V = 充分性:如果 U 是 X 中的任意开 集,则对于每一个 x∈U,由于U 是 x 的一个邻域,故存在 ,使得 . 于是 因此 ,故 U 是 B 中某些 元素之并,从而 B 是 X 的一个基. x x V U Vx B { } x x U x U U x V U = x x U U V = 充分性:如果 U 是 X 中的任意开 集,则对于每一个 x∈U,由于U 是 x 的一个邻域,故存在 ,使得 . 于是 因此 ,故 U 是 B 中某些 元素之并,从而 B 是 X 的一个基. x x V U Vx B { } x x U x U U x V U = x x U U V = 充分性:如果 U 是 X 中的任意开 集,则对于每一个 x∈U,由于U 是 x 的一个邻域,故存在 ,使得 . 于是 因此 ,故 U 是 B 中某些 元素之并,从而 B 是 X 的一个基. x x V U Vx B { } x x U x U U x V U = x x U U V = 充分性:如果 U 是 X 中的任意开 集,则对于每一个 x∈U,由于U 是 x 的一个邻域,故存在 ,使得 . 于是 因此 ,故 U 是 B 中某些 元素之并,从而 B 是 X 的一个基. x x V U Vx B { } x x U x U U x V U = x x U U V = 充分性:如果 U 是 X 中的任意开 集,则对于每一个 x∈U,由于U 是 x 的一个邻域,故存在 ,使得 . 于是 因此 ,故 U 是 B 中某些 元素之并,从而 B 是 X 的一个基. x x V U Vx B { } x x U x U U x V U = x x U U V = 充分性:如果 U 是 X 中的任意开 集,则对于每一个 x∈U,由于U 是 x 的一个邻域,故存在 ,使得 . 于是 因此 ,故 U 是 B 中某些 元素之并,从而 B 是 X 的一个基. x x V U Vx B { } x x U x U U x V U = x x U U V =

定理2.6.3设X是一个集合,B 是集合X的一个子集族.如果B满 足条件: (1)UBeB B=X (2)如果B,B2∈B,则对于任何 x∈B∩B2,存在B∈B使得 x∈BCB,∩B2
定理2.6.3 设 X 是一个集合,B 是集合 X 的一个子集族.如果 B 满 足条件: (1) ; (2) 如果 ,则对于任何 ,存在 使得 . BB B X = 1 2 B B, B 1 2 x B B BB 1 2 x B B B 定理2.6.3 设 X 是一个集合,B 是集合 X 的一个子集族.如果 B 满 足条件: (1) ; (2) 如果 ,则对于任何 ,存在 使得 . BB B X = 1 2 B B, B 1 2 x B B BB 1 2 x B B B 定理2.6.3 设 X 是一个集合,B 是集合 X 的一个子集族.如果 B 满 足条件: (1) ; (2) 如果 ,则对于任何 ,存在 使得 . BB B X = 1 2 B B, B 1 2 x B B BB 1 2 x B B B

则X的子集族 T=UCX|存在BucB使得U=UB} BeB U 是集合X的唯一的一个以B为基 的拓扑; 反之,如果X的一个子集族B是X 的某一个拓扑的基,则B一定满足 条件(1)和(2):
{U X | 存在 使得U B} B U T B U B B = = 则 X 的子集族 是集合 X 的唯一的一个以 B 为基 的拓扑; 反之,如果 X 的一个子集族B是 X 的某一个拓扑的基,则B一定满足 条件(1)和(2). {U X | 存在 使得U B} B U T B U B B = = 则 X 的子集族 是集合 X 的唯一的一个以 B 为基 的拓扑; 反之,如果 X 的一个子集族B是 X 的某一个拓扑的基,则B一定满足 条件(1)和(2)
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 2.7 拓扑空问中的序到.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 §2.5 内部、边界.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 §2.4 导集、闭集、闭包.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 §2.3 邻域与邻域系.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 §2.2 拓扑空间与连续映射.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 §2.1 度量空间与连续映射.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第一章 集合论初步 第六节 集族及其运算.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第一章 集合论初步 第五节 映射.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第一章 集合论初步 第四节 等价关系.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第一章 集合论初步 第三节 关系.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第一章 集合论初步 第一节 集合的基本概念.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)拓扑学引言(导论).ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(授课教案,孟晗).doc
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第三章 复变函数的积分 §3.3 Cauchy积分公式.ppt
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第三章 复变函数的积分 §3.2 柯西积分定理与原函数.ppt
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第三章 复变函数的积分 §3.1 复变函数的积分.ppt
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第二章 解析函数 §2.3 初等解析函数.ppt
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第二章 解析函数 §2.1 解析函数的概念.ppt
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第一章 复数与复变函数.ppt
- 运城学院:《复变函数论 Theory of Functions of Complex Variable》课程教学资源(讲义课件)复变函数复习(图片版).pdf
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第三章 子空间、积空间、商空间 §3.1 子空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第三章 子空间、积空间、商空间 §3.2(有限)积空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第三章 子空间、积空间、商空间 §3.3 商空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第四章 连通性 §4.1连通空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第四章 连通性 §4.2 连通性的某些简单应用.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第四章 连通性 §4.3 连通分支.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第四章 连通性 §4.4 局部连通空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第四章 连通性 §4.5 道路连通空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第五章 可数性公理 §5.1 第一与第二可数性公理.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第五章 可数性公理 §5.2 可分空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第五章 可数性公理 §5.3 Lindelöff 空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.1 T0 ,T1,Hausdorff空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.2 正则,正规,T3 ,T4空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.3 Urysohn引理和Tietze扩张定理.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.4 完全正则空间,Tychonoff空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.5 分离性公理与子空间,(有限)积空间和商空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.6 可度量化空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第七章 紧致性 §7.1 紧致空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第七章 紧致性 §7.2 紧致性与分离性公理.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第七章 紧致性 §7.3 n维欧氏空间Rn中的紧致子集.ppt
