《复变函数论 Theory of Functions of Complex Variable》课程教学资源（PPT课件讲稿）第三章 复变函数的积分 §3.3 Cauchy积分公式

§3.3 Cauchy和分公式 设f(z)在单连域D内解析，o∈D,则函数 f( 在处不解析。由复合闭路定理，设C z-20 是以为中心，δ为半径的正向圆周，则对任 意的6>0，积分重 dz取相同的积分值。 若让60，则z→2o,形式地有 如→4净 dz =f(3o)2πi

§3.3 Cauchy积分公式 设 f (z)在单连域D内解析， 0 z D  , 则函数 ( ) 0 f z z z − 在 z0 处不解析。由复合闭路定理，设C 0 是以 z 为中心，  为半径的正向圆周，则对任 意的   0, ( ) 0 d C f z z z z − 积分  取相同的积分值。 若让  → 0, 0 则 z z → ， 形式地有 ( ) 0 d c f z z z z −  ( 0 ) 0 d c f z z z z → −  ( 0 ) 0 1 d c f z z z z = −  =  f z( 0 ) 2πi

来 一、村西积分公式 定理3.7设f()在区域D内处处解析，C为D内的 任何一条正向简单曲线，它的内部完全含于D, 为C内的任一点，则： e-a (3.3.1) 证明由于f(②在z连续，任意 给定8>0，必存在一个6>0， 当2-0<δ时，有 f(z)-f(o)<ε 现以z为中心，R为半径作圆周K:2-o=R,使其 全部包含在C的内部，且R<δ，则有

D 0 0 1 ( ) ( ) d (3.3.1) 2πi ( ) C f z f z z z z = −  一 、柯西积分公式 定理3.7 设 f (z)在区域D内处处解析，C为D内的 任何一条正向简单曲线，它的内部完全含于D, z0为C内的任一点，则： 证明 K 0 z R z 由于 f (z)在z0 连续， 给定   0, 任意 必存在一个   0, 当 0 z z −   时，有 f z f z ( ) −  ( 0 )  现以z0为中心， 0 R 为半径作圆周K：z z R − = , 全部包含在C的内部， 使其 且 R  , 则有 C

米 9f7③+f.日e 2-20 =2i/()+f.0e-f4 2-20 而 29e4 <R-2w 由ε的任意性，有 )-f dz 0 z-20 所以 重/回=2e）

( ) ( ) 0 0 d d c K f z f z z z z z z z = − −   ( ) ( ) ( 0 ) 0 0 2πi d K f z f z f z z z z − = + −  ( 0 0 ) ( ) ( ) 0 0 d d K K f z f z f z z z z z z z − = + − −   ( ) ( ) ( ) ( 0 ) 0 0 0 d d K K f z f z f z f z z s z z z z − −  − −   2 K ds R   =   而 ( ) ( 0 ) 0 d 0 K f z f z z z z − = −  所以 ( ) 0 0 d 2πi ( ) c f z z f z z z = −  由  的任意性，有

米 说明 设区域D是简单闭曲线C的内部，f(z)在 D内解析，在闭区域D=D+C上连续， 则Cauchy积分公式(3.3.1)仍然成立。 ② 上述简单闭曲线可以是一个复合闭路， 即D不必是单连域。 3 Cauchyi积分公式(3.3.1)表明，解析函数 f(2)在C内部任意一点的值，完全由它 在其边界上的值所确定

说明 ① 设区域D是简单闭曲线C的内部，f (z)在 D内解析，在闭区域 D D C = + 上连续， 则Cauchy积分公式(3.3.1)仍然成立。 ② 即D不必是单连域。 上述简单闭曲线可以是一个复合闭路， ③ Cauchy积分公式(3.3.1)表明，解析函数 f (z)在C内部任意一点的值， 在其边界上的值所确定。 完全由它

米 例1计第称分1=小e-1e-2 dz 其中： 1)C是正向圆周|z=1/2 2)c是正向圆周z-1=1/4 3)C是正向圆周z=3 解：1)I=0(Cauchy7积分定理) 2）1=④n(e-1e-2 dz 1 -2）d=2元i1 =-2πi -2

例1 计算积分 d ( 1)( 2) C z I z z = − −  其中： 1）C是正向圆周 | z|=1 2 2）C是正向圆周 | z −1|=1 4 3）C是正向圆周 | z|= 3 解：1） I = 0 (Cauchy积分定理) 2） | 1| 1 4 1 d z ( 1)( 2) I z − = z z = − −  | 1| 1 4 1 ( 2) d z 1 z z − = z − = −  1 1 2πi 2πi 2 z z = = = − −

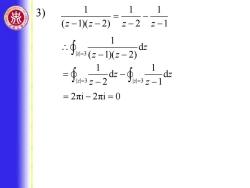
炭 3) 1 11 (z-1)(z-2)z-22-1 f.e--2 1 z =∮2-f止 =2πi-2πi=0

1 1 1 ( 1)( 2) 2 1 z z z z = − − − − − | | 3 | | 3 1 1 d d z z 2 1 z z z z = = = − − −   3) | | 3 1 d ( 1)( 2) z z z z =  − −  =−= 2πi 2πi 0

例2求下列积分的值： 米 (1I) 内fo-je dz 练(0乐止=2xn=0 2fo-je 2 -dz 2 9*品 π

例2 求下列积分的值： 2 sin z z dz z  = (1) ( )( ) 2 2 9 z z dz z z i = − + (2)  解 (1) 2 sin d z z z z  = 0 2 sin 0 z  i z = = = (2) ( )( ) 2 2 9 z z dz z z i = − +  ( ) 2 2 9 z z z dz z i = − = − −  2 2 9 5 z i z i z  = =  = − −

米 例3设 fe)=∮+)sin5d5, 151=2 5-2 求f'(①和f'(2+3i) 解：由Cauchyi积分公式和Cauchyi积分定理，有 2πi(z2+1)sinz2 f'①)=4πisinz+2iπ(z2+1)cosz =-4πSin1 f'(2+3i)=0

例3 设 2 | | 2 ( 1)sin f z( ) d , z      = + = −  解：由Cauchy积分公式和Cauchy积分定理，有 2 2πi( 1)sin 2 ( ) 0 2 z z z f z z  +  =    2 i (i) 4πi sin 2πi( 1)cos z f z z z z =  = + + 求 f (i) 和 f (2 3i) + f (2 3i) 0 + = = -4 sin1