聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第三章 子空间、积空间、商空间 §3.1 子空间

§3.1子空J 间
§3.1 子 空 间

定义3.1.1设(X,p)是一个度量空 间,Y是X的一个子集. 因此,Y×YcX×X.显然 prxy:Y×Y→R是Y的一个度量 称Y的度量pxy是由X的度量P诱导 出来的度量.度量空间(Y,pxxy称为 度量空间(X,p)的一个度量子空间
( , ) X Y Y X X | : Y Y Y Y R →| Y Y ( , | ) Y Y Y ( , ) X 定义3.1.1 设 是一个度量空 间,Y 是 X 的一个子集. 因此, . 显然 是Y 的一个度量. 称 Y 的度量 是由 X 的度量 诱导 出来的度量.度量空间 称为 度量空间 的一个度量子空间. ( , ) X Y Y X X | : Y Y Y Y R →| Y Y ( , | ) Y Y Y ( , ) X 定义3.1.1 设 是一个度量空 间,Y 是 X 的一个子集. 因此, . 显然 是Y 的一个度量. 称 Y 的度量 是由 X 的度量 诱导 出来的度量.度量空间 称为 度量空间 的一个度量子空间. ( , ) X Y Y X X | : Y Y Y Y R →| Y Y ( , | ) Y Y Y ( , ) X 定义3.1.1 设 是一个度量空 间,Y 是 X 的一个子集. 因此, . 显然 是Y 的一个度量. 称 Y 的度量 是由 X 的度量 诱导 出来的度量.度量空间 称为 度量空间 的一个度量子空间.

注意 >我们说度量空间Y是度量空间X的 一个度量子空间,意思就是Y是X 的一个子集,并且Y的度量是 由X的度量诱导出来的. >常将度量空间的任何一个非空子集 自动看作一个度量子空间
注 意 ➢我们说度量空间 Y 是度量空间 X的 一个度量子空间,意思就是 Y 是 X 的一个子集 , 并 且 Y 的度量是 由 X 的度量诱导出来的. ➢常将度量空间的任何一个非空子集 自动看作一个度量子空间

常见度量子空间 (1)(a,b),[a,b],(a,b] n+1 (2)S”={x=(x,x2,…,xn+)eR"|∑x2=1} i=1 (3)D={x=(x,x2,,x,)eR"2x<l -1 (4)E={x=(,x2,,xn)eR"|∑x≤1 i=l (5)(0,1)”,[0,1]
( , ),[ , ], ( , ] a b a b a b 1 1 2 1 2 1 1 { ( , , , ) | 1} n n n n i i S x x x x R x + + + = = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i D x x x x R x = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i E x x x x R x = = = (0,1) ,[0,1] n n 常见度量子空间 (1) (2) (3) (4) (5) ( , ),[ , ], ( , ] a b a b a b 1 1 2 1 2 1 1 { ( , , , ) | 1} n n n n i i S x x x x R x + + + = = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i D x x x x R x = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i E x x x x R x = = = (0,1) ,[0,1] n n 常见度量子空间 (1) (2) (3) (4) (5) ( , ),[ , ], ( , ] a b a b a b 1 1 2 1 2 1 1 { ( , , , ) | 1} n n n n i i S x x x x R x + + + = = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i D x x x x R x = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i E x x x x R x = = = (0,1) ,[0,1] n n 常见度量子空间 (1) (2) (3) (4) (5) ( , ),[ , ], ( , ] a b a b a b 1 1 2 1 2 1 1 { ( , , , ) | 1} n n n n i i S x x x x R x + + + = = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i D x x x x R x = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i E x x x x R x = = = (0,1) ,[0,1] n n 常见度量子空间 (1) (2) (3) (4) (5) ( , ),[ , ], ( , ] a b a b a b 1 1 2 1 2 1 1 { ( , , , ) | 1} n n n n i i S x x x x R x + + + = = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i D x x x x R x = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i E x x x x R x = = = (0,1) ,[0,1] n n 常见度量子空间 (1) (2) (3) (4) (5) ( , ),[ , ], ( , ] a b a b a b 1 1 2 1 2 1 1 { ( , , , ) | 1} n n n n i i S x x x x R x + + + = = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i D x x x x R x = = = 2 1 2 1 { ( , , , ) | 1} n n n n i i E x x x x R x = = = (0,1) ,[0,1] n n 常见度量子空间 (1) (2) (3) (4) (5)

定理3.1.1设Y是度量空间X的 一个度量子空间.则Y的子集U是Y 中的一个开集当且仅当存在一个X的 开集V使得U=/OY
定理3.1.1 设Y 是度量空间 X 的 一个度量子空间.则 Y 的子集U 是Y 中的一个开集当且仅当存在一个X 的 开集 V 使得 U V Y = . 定理3.1.1 设Y 是度量空间 X 的 一个度量子空间.则 Y 的子集U 是Y 中的一个开集当且仅当存在一个X 的 开集 V 使得 U V Y = . 定理3.1.1 设Y 是度量空间 X 的 一个度量子空间.则 Y 的子集U 是Y 中的一个开集当且仅当存在一个X 的 开集 V 使得 U V Y = . 定理3.1.1 设Y 是度量空间 X 的 一个度量子空间.则 Y 的子集U 是Y 中的一个开集当且仅当存在一个X 的 开集 V 使得 U V Y = . 定理3.1.1 设Y 是度量空间 X 的 一个度量子空间.则 Y 的子集U 是Y 中的一个开集当且仅当存在一个X 的 开集 V 使得 U V Y =

定义3.12设A是一个集族,Y是 一个集合.集族 {A∩Y|A∈A} 称为A在集合Y上的限制,记作A. 例:A={{1},{2,3},{1,2}{2,5},1,2,5} Y={1,2,3,6} A1y={{1},{2,3},{L,2,2}
定义3.1.2 设 A 是一个集族,Y 是 一个集合. 集族 称为 A 在集合 Y 上的限制,记作 . 例: { | } A Y A A A| Y A ={{1},{2,3},{1, 2},{2,5},{1, 2,5}} Y ={1, 2,3, 6} A | {{1},{2,3},{1, 2},{2}} Y = 定义3.1.2 设 A 是一个集族,Y 是 一个集合. 集族 称为 A 在集合 Y 上的限制,记作 . 例: { | } A Y A A A| Y A ={{1},{2,3},{1, 2},{2,5},{1, 2,5}} Y ={1, 2,3, 6} A | {{1},{2,3},{1, 2},{2}} Y = 定义3.1.2 设 A 是一个集族,Y 是 一个集合. 集族 称为 A 在集合 Y 上的限制,记作 . 例: { | } A Y A A A| Y A ={{1},{2,3},{1, 2},{2,5},{1, 2,5}} Y ={1, 2,3, 6} A | {{1},{2,3},{1, 2},{2}} Y = 定义3.1.2 设 A 是一个集族,Y 是 一个集合. 集族 称为 A 在集合 Y 上的限制,记作 . 例: { | } A Y A A A| Y A ={{1},{2,3},{1, 2},{2,5},{1, 2,5}} Y ={1, 2,3, 6} A | {{1},{2,3},{1, 2},{2}} Y = 定义3.1.2 设 A 是一个集族,Y 是 一个集合. 集族 称为 A 在集合 Y 上的限制,记作 . 例: { | } A Y A A A| Y A ={{1},{2,3},{1, 2},{2,5},{1, 2,5}} Y ={1, 2,3, 6} A | {{1},{2,3},{1, 2},{2}} Y = 定义3.1.2 设 A 是一个集族,Y 是 一个集合. 集族 称为 A 在集合 Y 上的限制,记作 . 例: { | } A Y A A A| Y A ={{1},{2,3},{1, 2},{2,5},{1, 2,5}} Y ={1, 2,3, 6} A | {{1},{2,3},{1, 2},{2}} Y = 定义3.1.2 设 A 是一个集族,Y 是 一个集合. 集族 称为 A 在集合 Y 上的限制,记作 . 例: { | } A Y A A A| Y A ={{1},{2,3},{1, 2},{2,5},{1, 2,5}} Y ={1, 2,3, 6} A | {{1},{2,3},{1, 2},{2}} Y =

引理3.1.2设Y是拓扑空间(X,T) 的一个子集,则集族Tx是Y的一个拓 扑. 证明()由于Y=X∩Y,且X∈T, 故Y∈Tly.又因为中=中OY, 且∈T,故eT|y;
引理3.1.2 设Y 是拓扑空间 的一个子集, 则集族 是Y 的一个拓 扑. 证明 (i) 由于 ,且 , 故 . 又因为 , 且 , 故 ; ( , ) X T T | Y Y X Y = X T Y T| Y = Y T T| Y 引理3.1.2 设Y 是拓扑空间 的一个子集, 则集族 是Y 的一个拓 扑. 证明 (i) 由于 ,且 , 故 . 又因为 , 且 , 故 ; ( , ) X T T | Y Y X Y = X T Y T| Y = Y T T| Y 引理3.1.2 设Y 是拓扑空间 的一个子集, 则集族 是Y 的一个拓 扑. 证明 (i) 由于 ,且 , 故 . 又因为 , 且 , 故 ; ( , ) X T T | Y Y X Y = X T Y T| Y = Y T T| Y 引理3.1.2 设Y 是拓扑空间 的一个子集, 则集族 是Y 的一个拓 扑. 证明 (i) 由于 ,且 , 故 . 又因为 , 且 , 故 ; ( , ) X T T | Y Y X Y = X T Y T| Y = Y T T| Y 引理3.1.2 设Y 是拓扑空间 的一个子集, 则集族 是Y 的一个拓 扑. 证明 (i) 由于 ,且 , 故 . 又因为 , 且 , 故 ; ( , ) X T T | Y Y X Y = X T Y T| Y = Y T T| Y

()若A,B∈Ty,即存在A,B,∈T 使得A=AOY,B=B,∩Y 于是AOB=(A⌒B)OY 由于AOB∈T,故A∩B∈T|y. ()若T1是集族T|y的一个子集族, 即对于每一个A∈T1,存在A 使得A=A∩Y.因此 UA=U(4∩Y)=(UA)⌒Y∈T A∈T1 A∈T1 AET
(ii) 若 ,即存在 使得 于是 由于 ,故 . (iii) 若 是集族 的一个子集族, 即对于每一个 ,存在 使得 . 因此 , A BT| Y 1 1 A B, T 1 1 A A Y B B Y = = , 1 1 A B A B Y = ( ) A B 1 1 T A B T| Y T1 T| Y AT1 A1 A A Y = 1 1 1 1 1 1 ( ) ( ) T T T T|Y A A A A A Y A Y = = (ii) 若 ,即存在 使得 于是 由于 ,故 . (iii) 若 是集族 的一个子集族, 即对于每一个 ,存在 使得 . 因此 , A BT| Y 1 1 A B, T 1 1 A A Y B B Y = = , 1 1 A B A B Y = ( ) A B 1 1 T A B T| Y T1 T| Y AT1 A1 A A Y = 1 1 1 1 1 1 ( ) ( ) T T T T|Y A A A A A Y A Y = = (ii) 若 ,即存在 使得 于是 由于 ,故 . (iii) 若 是集族 的一个子集族, 即对于每一个 ,存在 使得 . 因此 , A BT| Y 1 1 A B, T 1 1 A A Y B B Y = = , 1 1 A B A B Y = ( ) A B 1 1 T A B T| Y T1 T| Y AT1 A1 A A Y = 1 1 1 1 1 1 ( ) ( ) T T T T|Y A A A A A Y A Y = = (ii) 若 ,即存在 使得 于是 由于 ,故 . (iii) 若 是集族 的一个子集族, 即对于每一个 ,存在 使得 . 因此 , A BT| Y 1 1 A B, T 1 1 A A Y B B Y = = , 1 1 A B A B Y = ( ) A B 1 1 T A B T| Y T1 T| Y AT1 A1 A A Y = 1 1 1 1 1 1 ( ) ( ) T T T T|Y A A A A A Y A Y = = (ii) 若 ,即存在 使得 于是 由于 ,故 . (iii) 若 是集族 的一个子集族, 即对于每一个 ,存在 使得 . 因此 , A BT| Y 1 1 A B, T 1 1 A A Y B B Y = = , 1 1 A B A B Y = ( ) A B 1 1 T A B T| Y T1 T| Y AT1 A1 A A Y = 1 1 1 1 1 1 ( ) ( ) T T T T|Y A A A A A Y A Y = = (ii) 若 ,即存在 使得 于是 由于 ,故 . (iii) 若 是集族 的一个子集族, 即对于每一个 ,存在 使得 . 因此 , A BT| Y 1 1 A B, T 1 1 A A Y B B Y = = , 1 1 A B A B Y = ( ) A B 1 1 T A B T| Y T1 T| Y AT1 A1 A A Y = 1 1 1 1 1 1 ( ) ( ) T T T T|Y A A A A A Y A Y = = (ii) 若 ,即存在 使得 于是 由于 ,故 . (iii) 若 是集族 的一个子集族, 即对于每一个 ,存在 使得 . 因此 , A BT| Y 1 1 A B, T 1 1 A A Y B B Y = = , 1 1 A B A B Y = ( ) A B 1 1 T A B T| Y T1 T| Y AT1 A1 A A Y = 1 1 1 1 1 1 ( ) ( ) T T T T|Y A A A A A Y A Y = = (ii) 若 ,即存在 使得 于是 由于 ,故 . (iii) 若 是集族 的一个子集族, 即对于每一个 ,存在 使得 . 因此 , A BT| Y 1 1 A B, T 1 1 A A Y B B Y = = , 1 1 A B A B Y = ( ) A B 1 1 T A B T| Y T1 T| Y AT1 A1 A A Y = 1 1 1 1 1 1 ( ) ( ) T T T T|Y A A A A A Y A Y = = (ii) 若 ,即存在 使得 于是 由于 ,故 . (iii) 若 是集族 的一个子集族, 即对于每一个 ,存在 使得 . 因此 , A BT| Y 1 1 A B, T 1 1 A A Y B B Y = = , 1 1 A B A B Y = ( ) A B 1 1 T A B T| Y T1 T| Y AT1 A1 A A Y = 1 1 1 1 1 1 ( ) ( ) T T T T|Y A A A A A Y A Y = = (ii) 若 ,即存在 使得 于是 由于 ,故 . (iii) 若 是集族 的一个子集族, 即对于每一个 ,存在 使得 . 因此 , A BT| Y 1 1 A B, T 1 1 A A Y B B Y = = , 1 1 A B A B Y = ( ) A B 1 1 T A B T| Y T1 T| Y AT1 A1 A A Y = 1 1 1 1 1 1 ( ) ( ) T T T T|Y A A A A A Y A Y = = (ii) 若 ,即存在 使得 于是 由于 ,故 . (iii) 若 是集族 的一个子集族, 即对于每一个 ,存在 使得 . 因此 , A BT| Y 1 1 A B, T 1 1 A A Y B B Y = = , 1 1 A B A B Y = ( ) A B 1 1 T A B T| Y T1 T| Y AT1 A1 A A Y = 1 1 1 1 1 1 ( ) ( ) T T T T|Y A A A A A Y A Y = =

综上有T|x是Y的拓扑 定义3.1.3设Y是拓扑空间(X,T) 的一个子集.Y的拓扑Ty称为(相对于 X的拓扑T而言的)相对拓扑: 拓扑空间(Y,T|y)称为拓扑空间X的 一个(拓扑)子空间
综上有 是Y 的拓扑. 定义3.1.3 设Y 是拓扑空间 的一个子集. Y 的拓扑 称为(相对于 X的拓扑 而言的)相对拓扑; 拓扑空间 称为拓扑空间 X 的 一个(拓扑)子空间. T | Y ( , ) X T T | Y T ( , ) Y T | Y 综上有 是Y 的拓扑. 定义3.1.3 设Y 是拓扑空间 的一个子集. Y 的拓扑 称为(相对于 X的拓扑 而言的)相对拓扑; 拓扑空间 称为拓扑空间 X 的 一个(拓扑)子空间. T | Y ( , ) X T T | Y T ( , ) Y T | Y 综上有 是Y 的拓扑. 定义3.1.3 设Y 是拓扑空间 的一个子集. Y 的拓扑 称为(相对于 X的拓扑 而言的)相对拓扑; 拓扑空间 称为拓扑空间 X 的 一个(拓扑)子空间. T | Y ( , ) X T T | Y T ( , ) Y T | Y 综上有 是Y 的拓扑. 定义3.1.3 设Y 是拓扑空间 的一个子集. Y 的拓扑 称为(相对于 X的拓扑 而言的)相对拓扑; 拓扑空间 称为拓扑空间 X 的 一个(拓扑)子空间. T | Y ( , ) X T T | Y T ( , ) Y T | Y 综上有 是Y 的拓扑. 定义3.1.3 设Y 是拓扑空间 的一个子集. Y 的拓扑 称为(相对于 X的拓扑 而言的)相对拓扑; 拓扑空间 称为拓扑空间 X 的 一个(拓扑)子空间. T | Y ( , ) X T T | Y T ( , ) Y T | Y 综上有 是Y 的拓扑. 定义3.1.3 设Y 是拓扑空间 的一个子集. Y 的拓扑 称为(相对于 X的拓扑 而言的)相对拓扑; 拓扑空间 称为拓扑空间 X 的 一个(拓扑)子空间. T | Y ( , ) X T T | Y T ( , ) Y T | Y 综上有 是Y 的拓扑. 定义3.1.3 设Y 是拓扑空间 的一个子集. Y 的拓扑 称为(相对于 X的拓扑 而言的)相对拓扑; 拓扑空间 称为拓扑空间 X 的 一个(拓扑)子空间. T | Y ( , ) X T T | Y T ( , ) Y T | Y
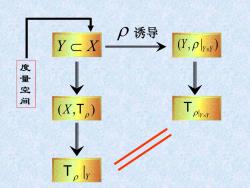
P诱导 YCX (Ypa) 度量空间 (X,T) Toly
Y X 度 量 空 间 诱导 ( , | ) Y Y Y T | Y Y ( , ) X T T | Y
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 2.6 基与于基.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 2.7 拓扑空问中的序到.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 §2.5 内部、边界.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 §2.4 导集、闭集、闭包.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 §2.3 邻域与邻域系.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 §2.2 拓扑空间与连续映射.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第二章 度量空间与连续映射 §2.1 度量空间与连续映射.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第一章 集合论初步 第六节 集族及其运算.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第一章 集合论初步 第五节 映射.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第一章 集合论初步 第四节 等价关系.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第一章 集合论初步 第三节 关系.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第一章 集合论初步 第一节 集合的基本概念.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)拓扑学引言(导论).ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(授课教案,孟晗).doc
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第三章 复变函数的积分 §3.3 Cauchy积分公式.ppt
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第三章 复变函数的积分 §3.2 柯西积分定理与原函数.ppt
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第三章 复变函数的积分 §3.1 复变函数的积分.ppt
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第二章 解析函数 §2.3 初等解析函数.ppt
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第二章 解析函数 §2.1 解析函数的概念.ppt
- 《复变函数论 Theory of Functions of Complex Variable》课程教学资源(PPT课件讲稿)第一章 复数与复变函数.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第三章 子空间、积空间、商空间 §3.2(有限)积空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第三章 子空间、积空间、商空间 §3.3 商空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第四章 连通性 §4.1连通空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第四章 连通性 §4.2 连通性的某些简单应用.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第四章 连通性 §4.3 连通分支.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第四章 连通性 §4.4 局部连通空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第四章 连通性 §4.5 道路连通空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第五章 可数性公理 §5.1 第一与第二可数性公理.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第五章 可数性公理 §5.2 可分空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第五章 可数性公理 §5.3 Lindelöff 空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.1 T0 ,T1,Hausdorff空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.2 正则,正规,T3 ,T4空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.3 Urysohn引理和Tietze扩张定理.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.4 完全正则空间,Tychonoff空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.5 分离性公理与子空间,(有限)积空间和商空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第六章 分离性公理 §6.6 可度量化空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第七章 紧致性 §7.1 紧致空间.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第七章 紧致性 §7.2 紧致性与分离性公理.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第七章 紧致性 §7.3 n维欧氏空间Rn中的紧致子集.ppt
- 聊城大学:《拓扑学 Topology》课程教学资源(PPT课件讲稿)第七章 紧致性 §7.4 几种紧致性以及其间的关系.ppt
