聊城大学：《拓扑学 Topology》课程教学资源（PPT课件讲稿）第六章 分离性公理 §6.2 正则，正规，T3 ,T4空间

§6.2正则，正规，T3,T4空间 定义6.2.1 设X是一个拓扑空间， A,UcX.若AC乙U°，则称U是 集合A的一个邻域. 换言之 特别的，若还是一个开集（闭集）， 则称U是A的一个开（闭）邻域： 继续

§6.2 正则，正规，T3 ,T4空间 定义6.2.1 设X是一个拓扑空间， . 若 ，则称U是 集合A的一个邻域. 特别的，若U还是一个开集（闭集）， 则称U是A的一个开（闭）邻域. A U X ,  A U  换言之 继续

也可以换一个说法 若存在一个开集满足： ACYCU 则称U是A的一个邻域。 心

也可以换一个说法 若存在一个开集V满足: 则称U是A的一个邻域. A V U  

定义6.2.2 设X是一个拓扑空 间，若X中的任何一个点x和任何 一个不包含x的闭集A都各有一个 开邻域U,V,使得U⌒V=Φ 则称X是一个正则空间

定义6.2.2 设X是一个拓扑空 间，若X中的任何一个点x和任何 一 个不包含x的闭集A都各有一个 开邻域U,V，使 得 ， 则称X是一个 . U V = 

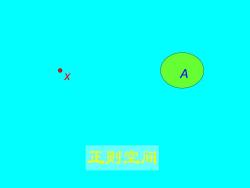
X A 正则空间

x A

定理6.2.1X是一个拓扑空间 则X是一个正则空间当且仅当对于 任何点x∈X和x的任意一个邻 域U,存在一个x的开邻域V使得：

定理6.2.1 是一个拓扑空间, 则 是一个正则空间当且仅当对于 任 何点 和 的任意一个邻 域U,存在一个 的开邻域V使得: V U x X  x x X X

证明：必要性设X是一个正则空 间，U是x的任何一个开邻域，则U是 不包含x的闭集 图示 从而x和U分别有开邻域V和V使 得VOY=Φ，从而V二Y' 所以VcY=cU 继续

证明: 必要性 设X是一个正则空 间,U是 x 的任何一个开邻域,则 是 不包含 x 的闭集, 从而 x 和 分别有开邻域 和 使 得 ,从而 , 所以 . U U V V1 V V  =  1 V V1   V V V U 1 1 − −  =    图示 继续

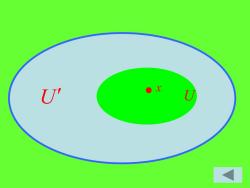
U' ●x U

x U  U

充分性对任意的x∈X和不包含x 的任意闭集A,则A'是x的一个开邻域， 故有x的开邻域U使得UcA', 令 =乙- 则有AcY,所以V是A 的一个开邻域，并且有UOV= 这说明X是一个正则空间： 继续

充分性 对任意的x∈X和不包含x 的任意闭集A,则 是x的一个开邻域, 故有x的开邻域U 使得 , 令 ,则有 ,所以V是A 的一个开邻域,并且有 , 这说明X是一个正则空间. A U A   ' V U − = A V  U V =  图 继续

A A ●比

A x A

定义6.23 设X是一个拓扑空间， 若X中任意两个互不相交的闭集A、B 都各有一个开邻域U、V,满足 U⌒V=( 则称拓扑空间X是一个正规空间

定义6.2.3 设X是一个拓扑空间, 若X中任意两个互不相交的闭集A、B 都各有一个开邻域U、V，满足 则称拓扑空间X 是一个正规空间. U V = 