《水文地质学基础》课程授课教案（讲稿）第四章 地下水运动的基本规律 §1 水力学的基本概念 §2 重力水运动的基本规律

课程名称：水文地质学基础第4 讲次第四章地下水运动的基本规律授课题目(章、节)S1水力学的基本概念S2重力水运动的基本规律本讲目的及重点：【目的要求]：通过本讲学习，使学生掌握地下水水头及其构成、水力梯度及其意义：掌握达西定律并认识地下水线性流动的特点。[重点]：地下水水头及其构成、水力梯度及其意义，达西定律及其适用性[难点]：地下水水头及其构成、水力梯度，线性地下水流的特点内容备注[本讲内容的引入】地下水在各种因素的影响下经常处于不断运动之中。地下水的运动使其水量和水质发生变化、并产生地质作用，改造着周围环境。研究地下水的运动无论在理论上还是在实际问题中部具有重要意义，它是水文地质学重要的组成部分，并已成为一门独立的学科一一地下水动力学。在水文地质工作中，诸如矿坑涌水量预测、水资源评价、地下水动态预报或水质变化预测等等方面，都与重力地下水的运动密切相关。在此只讨论液态重力地下水的运动。[本讲内容]s1水力学的基本概念一、静止液体的位置高度、测压管高度、测压管水头图见PPT1、概念装有静止液体的容器\液面之下任意不同高度的A、B两处I假定管内的毛细现象可以忽略不计测压管在容器底而以下，取任一水平面OO作为基准面，（1）位置高度：A点到基准面的垂直距,用ZA表示，其量纲为[L]。（2）测压管高度：A点到测压管液面之间的高度，用表示，其中PA代表A点处液体Y本身所形成的压强，其量纲为[]（3）测压管水头：位置高度与测压管高度之和。静止液体中各点的测压管水头为一常数

课程名称:水文地质学基础 第 4 讲次 授课题目(章、节) 第四章 地下水运动的基本规律 §1 水力学的基本概念 §2 重力水运动的基本规律 本讲目的及重点： [目的要求]： 通过本讲学习，使学生掌握地下水水头及其构成、水力梯度及其意义；掌握达西定律并认 识地下水线性流动的特点。 [重点]： 地下水水头及其构成、水力梯度及其意义，达西定律及其适用性 [难点]： 地下水水头及其构成、水力梯度，线性地下水流的特点 内 容 备 注 [本讲内容的引入] 地下水在各种因素的影响下经常处于不断运动之中。地下水的运动使其 水量和水质发生变化、并产生地质作用，改造着周围环境。研究地下水的运动无论在理论 上还是在实际问题中部具有重要意义，它是水文地质学重要的组成部分，并已成为一门独 立的学科——地下水动力学。在水文地质工作中，诸如矿坑涌水量预测、水资源评价、地 下水动态预报或水质变化预测等等方面，都与重力地下水的运动密切相关。在此只讨论液 态重力地下水的运动。 [本讲内容] §1 水力学的基本概念 一、静止液体的位置高度、测压管高度、测压管水头 图见 PPT 1、概念 装有静止液体的容器\液面之下任意不同高度的 A、B 两处\假定管内的毛细现象可以忽 略不计\测压管\在容器底而以下，取任一水平面 OO’作为基准面。 （1）位置高度：A 点到基准面的垂直距,用 ZA 表示，其量纲为[L]。 （2）测压管高度：A 点到测压管液面之间的高度，用  PA 表示，其中 PA 代表 A 点处液体 本身所形成的压强，其量纲为[L] （3）测压管水头：位置高度与测压管高度之和。 静止液体中各点的测压管水头为一常数

+P4=Zo+PZ.1112、位置高度、测压管高度、测压管水头的物理意义（1）位置高度Z：代表相对于基准面的单位位置势能位置势能=mgZ，单位重力(mg=1)的液体（2）测压管高度一：代表压能。因取单位重力(mg=1)，称为单为压能。（3）测压管水头：是位置高度Z与测压管高度之和，代表单位重力液体的总势能P一压能的作用，使得在该点处安上测压管后液体便沿测压管上升到的高度，压能便转化y为位置势能。静止液体内各点的单位总势能是相等的，这是静水力学中的能量守恒定律，二、稳定流及其运动的能量方程1.概念稳定流：在流场中，任何固定空间点的流速、流量及动水压强（运动液体内任一点的压应力）等所有运动要素都不随时间变化的液体流动。运动要素仅是空间坐标的函数，而与时间无关。非稳定流：如果有任一运动要素随时间而变化。2.稳定液流的能量方程稳定液流的能量方程反映了液体运动中能量守恒与转化关系的规律，它是由瑞士科学家伯诺里(Bernoulli)于1738年根据动能定理推导出来的，故又叫伯诺里方程.在推导过程中，伯诺里作了如下假定：①液体是不可压缩的理想液体：②液流是稳定流：③液体运动为缓变流，其中的流线几乎是相互平行的，并且曲率很小，流线几乎都是直线：流量沿程不变。根据动能定理及上述假定，伯诺里把液流过水断面（即与液流的所有流线构成正交的横断面)上单位重量液体所具有的机械能表达为：P+av?H=Z+-y2g式中，g—一重力加速V一一液流过水断面的平均流速

  B B A A P Z P Z + = + 2、位置高度、测压管高度、测压管水头的物理意义 （1）位置高度 Z：代表相对于基准面的单位位置势能． 位置势能=mgZ，单位重力(mg=1)的液体 （2）测压管高度  P ：代表压能。因取单位重力(mg=1)，称为单为压能。 （3）测压管水头：是位置高度 Z 与测压管高度之和，代表单位重力液体的总势能．  P 压能的作用，使得在该点处安上测压管后液体便沿测压管上升到的高度，压能便转化 为位置势能。 静止液体内各点的单位总势能是相等的，这是静水力学中的能量守恒定律． 二、稳定流及其运动的能量方程 1．概念 稳定流：在流场中，任何固定空间点的流速、流量及动水压强(运动液体内任一点的压应力) 等所有运动要素都不随时间变化的液体流动。运动要素仅是空间坐标的函数，而与时间无 关。 非稳定流：如果有任一运动要素随时间而变化。 2．稳定液流的能量方程 稳定液流的能量方程反映了液体运动中能量守恒与转化关系的规律，它是由瑞士科 学家伯诺里(Bernoulli)于 1738 年根据动能定理推导出来的，故又叫伯诺里方程． 在推导过程中，伯诺里作了如下假定：①液体是不可压缩的理想液体：②液流是稳 定流：⑥液体运动为缓变流，其中的流线几乎是相互平行的，并且曲率很小，流线几乎都 是直线：流量沿程不变。根据动能定理及上述假定，伯诺里把液流过水断面(即与液流的所 有流线构成正交的横断面)上单位重量液体所具有的机械能表达为： g P aV H Z 2 2 = + +  式中，g——重力加速 V——液流过水断面的平均流速

a一一动能修正系数（修正用过水断面的平均流速代替实际流速所造成的偏差.其位大小取决于断面上流速的分布状况，分布愈均匀，值愈接近于1，一般情况下为a=1.06一1.10av?一为速度水头。2gH称为总水头，它代表着过水断面上单位重力液体所具有的总机械能。如果在缓变流的实际水流中，沿流向任取两个过水断面1一1和2一2，两断面的总水头分别以HI、H2表示，则通过两断面的能量方程可表达如下：Hi=H2十 hw1-2或Z+4+笨=Z.++等签+hu12g2g式中hw1-2是平均单位重力液体从断面1—1流到断面2—2过程中，由于克服水流摩擦阻力而消耗的机械能。这部分机械能转化为热能而散失，称为水头损失。该方程为稳定液流的能量方程，它是研究液体运动（包括地下水运动）规律的基本方程之一.三、地下水水头、水力梯度P.av?H=Z+-y2g水头：是表示液流中某点位能、压能、动能的总和，在研究地下水运动时，考虑到在一般情况下地下水运动的速度比较缓慢，渗透流速则更小，上式中的速度水头相对于测压水头是微不足道的，故可略去速度水头，用测压水头近似代表总水头：即，1、地下水水头：H=Z+PY2、水力梯度：图见PPT沿流线方向，ab为地下水水头线。水头线上某点的曲率即为该点的水力梯度/水力梯度就是沿地下水流方向上单位渗透途径上的水头损失。I=_dhds

a——动能修正系数(修正用过水断面的平均流速代替实际流速所造成的偏差．其位大 小取决于断面上流速的分布状况，分布愈均匀，值愈接近于 1，一般情况下为 a=1．06—1．10， g aV 2 2 为速度水头。 H 称为总水头，它代表着过水断面上单位重力液体所具有的总机械能。 如果在缓变流的实际水流中，沿流向任取两个过水断面 1—1 和 2—2，两断面的总水 头分别以 H1、H2 表示，则通过两断面的能量方程可表达如下： H1=H2 十 hw1-2 或 1 2 2 2 2 2 2 2 1 1 1 1 2 2 + + = + + + hw − g P a V Z g P a V Z   式中 hw1-2 是平均单位重力液体从断面 1—1 流到断面 2—2 过程中，由于克服水流摩擦阻力 而消耗的机械能。这部分机械能转化为热能而散失，称为水头损失。 该方程为稳定液流的能量方程，它是研究液体运动(包括地下水运动)规律的基本方程 之一． 三、地下水水头、水力梯度 g P aV H Z 2 2 = + +  水头：是表示液流中某点位能、压能、动能的总和． 在研究地下水运动时，考虑到在一般情况下地下水运动的速度比较缓慢，渗透流速则 更小，上式中的速度水头相对于测压水头是微不足道的，故可略去速度水头，用测压水头 近似代表总水头．即，1、地下水水头：  P H = Z + 2、水力梯度： 图见 PPT 沿流线方向，ab 为地下水水头线。 水头线上某点的曲率即为该点的水力梯度/水力梯度就是沿地下水流方向上单位渗透 途径上的水头损失。 dS dh I = −

式中：I一一水力梯度（无量纲）：dS—一渗透途径上无限小的长度[]dh——ds长度上的水头变化值[L]严格说来，ds应是弧形线段，因为一般情况下水力梯度很小，故在实际确定水力梯度时，常用水平长度代替渗透途径上的长度，用平均水力梯度代替微分水力梯度：如图4一5所示，A、B是沿地下水流向所分布的两个钻孔，其水头值分别为ha、hb，两孔的水平距离为L，则两孔间的平均水力梯度便是I=h-hL32重力水运动的基本规律渗流与渗流场：地下水在岩石空隙中的运动称为渗流（渗透）。发生渗流的区域称为渗流场。流体运动可分为层流与紊流。在岩层空隙中渗流时，水的质点作有秩序的、互不混杂的流动，称为层流。在具狭小空隙的岩石（如砂岩孔隙、狭窄裂隙）中流动时，重力水受介质的吸引力较大，水的质点排列较有秩序，作层流运动。水的质点无秩序地、互相混杂的流动，称为紊流运动。紊流运动时，水流所受阻力比层流状态大，消耗的能量较多。在宽大的空隙中，水的流速较大时，容易呈素流运动。1.达西定律：1856年，法国水力学家达西由大量试验得到的地下水的线性渗透基本定律h=KolQ=K0L式中，Q一一渗透流量(出口处流量即为通过砂柱各断面的流量)：の一一过水断面（在实验中相当于砂柱横断面积）：h——水头损失(h=H一H2，即上下游过水断面的水头差）L一一渗透长度(上下游过水断面的距离)；I—一水力坡度(即水头差除以渗透长度)，K一一渗透系数。此即达西公式。从水力学已知，通过某一断面的流量Q等于流速与过水断面面积的乘积，即：

式中：I——水力梯度（无量纲）； dS——渗透途径上无限小的长度[L] dh——dS 长度上的水头变化值[L] 严格说来，ds 应是弧形线段，因为一般情况下水力梯度很小，故在实际确定水力梯度 时，常用水平长度代替渗透途径上的长度，用平均水力梯度代替微分水力梯度．如图 4—5 所示，A、B 是沿地下水流向所分布的两个钻孔，其水头值分别为 ha、hb，两孔的水平距 离为 L，则两孔间的平均水力梯度便是： L h h I a − b = §2 重力水运动的基本规律 渗流与渗流场：地下水在岩石空隙中的运动称为渗流(渗透)。发生渗流的区域称为渗 流场。 流体运动可分为层流与紊流。 在岩层空隙中渗流时，水的质点作有秩序的、互不混杂的 流动，称为层流。在具狭小空隙的岩石（如砂岩孔隙、狭窄裂隙）中流动时，重力水受介 质的吸引力较大，水的质点排列较有秩序，作层流运动。水的质点无秩序地、互相混杂的 流动，称为紊流运动。紊流运动时，水流所受阻力比层流状态大，消耗的能量较多。在宽 大的空隙中，水的流速较大时，容易呈紊流运动。 1.达西定律： 1856 年,法国水力学家达西由大量试验得到的地下水的线性渗透基本定律: K I L h Q = K =  式中, Q ——渗透流量(出口处流量即为通过砂柱各断面的流量)；  ——过水断面(在实验中相当于砂柱横断面积)； h——水头损失(h＝Hl 一 H2，即上下游过水断面的水头差) L——渗透长度(上下游过水断面的距离)； I——水力坡度(即水头差除以渗透长度)， K——渗透系数。 此即达西公式。 从水力学已知，通过某一断面的流量 Q 等于流速与过水断面面积的乘积，即：

Q=@V则V=Q/0V=KI达西定律也可以另一种形式表达之：V称作渗透流速，其余各项意义同前。2.渗透流速：图4-20=one水流实际流过的为扣除结合水所占据的范围以外的空隙面积，o'=onen。为有效空隙度，为重力水流动的空隙体积与岩石体积之比。孔隙度n：结合水、重力水所占据的空间与岩石体积之比。。给水度U：除结合水、毛细水、孔角毛细水之外μ<n,<n只有空隙大的岩层：μ～n。n可知V并不是真实流速，而是假设水流通过包括骨架与空隙在内的断面(の)时所具有的-一种虚拟流速。假设实际流速为u，即：Q='u则のV=のu因为α'=on则V=n.u3.水力梯度I：沿渗透途径水头损失与相应渗透途径长度的比值。I=h_H-H2LL水流通过单位长度渗透途径为克服摩擦阻力所耗失的机械能。驱动力，即克服摩擦阻力使水以一定速度流动的力量。4.渗透系数V=KI，1无量纲，K表示水力梯度等于1时的渗透流速。单位为m/d，cm/s。渗透系数可定量说明岩石的渗透性能

Q = V 则 V = Q / 达西定律也可以另一种形式表达之: V = KI V 称作渗透流速，其余各项意义同前。 2.渗透流速：图 4-2  = ne 水流实际流过的为扣除结合水所占据的范围以外的空隙面积,  = ne  e n 为有效空隙度，为重力水流动的空隙体积与岩石体积之比。 孔隙度 n：结合水、重力水所占据的空间与岩石体积之比。 给水度μ：除结合水、毛细水、孔角毛细水之外 μ< e n <n 只有空隙大的岩层: μ≈ e n ≈n 可知 V 并不是真实流速,而是假设水流通过包括骨架与空隙在内的断面(  )时所具有的一 种虚拟流速。假设实际流速为 u，即： Q = u 则 V = u 因为  = ne  则 V = ne u 3． 水力梯度 I：沿渗透途径水头损失与相应渗透途径长度的比值。 L H H L h I 1 − 2 = = 水流通过单位长度渗透途径为克服摩擦阻力所耗失的机械能。 驱动力，即克服摩擦阻力使水以一定速度流动的力量。 4． 渗透系数 V = KI ， I 无量纲，K 表示水力梯度等于 1 时的渗透流速。单位为 m/d，cm/s。 渗透系数可定量说明岩石的渗透性能

根据K值大小，可将岩石分为以下几类：K>10米/日如粗砂、砾、岩溶发育岩石强透水岩石透水岩石K=10一1米/日如砂、裂隙发育岩石微透水岩石K=1—0.01米/日如亚砂土、裂隙发育微弱岩石透水极弱岩石X=0.01一0.001米/日如亚粘土，粘土，淤泥不透水岩石K2320为紊流实际资料表明，自然界中的孔隙岩层、裂隙岩层以及溶穴不十分发育的岩溶岩层中的地下水运动基本上部属层流运动。仅在溶洞发育和粗大的卵砾石岩层中才会形成局部的紊流运动。因此，达西公式能广泛地应用于自然界中的地下水计算。可以说，达西定律是定性分析水文地质问题和定量研究地下水运动规律的最基本定律，【课程小结本讲讲述了地下水水头及其构成、水力梯度及其意义；重点讲述达西定律，地下水线性流动，达西定律的适用性。[本讲作业及要求]：（1）请对比以下概念渗透流速与实际流速；渗透系数与渗透率：水头与水位（2）达西定律的应用

根据 K 值大小，可将岩石分为以下几类: 强透水岩石 K＞10 米／日 如粗砂、砾、岩溶发育岩石 透水岩石 K=10 一 1 米／日 如砂、裂隙发育岩石 微透水岩石 K＝l—0 .01 米／日如亚砂土、裂隙发育微弱岩石 透水极弱岩石 X＝0．01 一 0．001 米／日如亚粘土，粘土，淤泥 不透水岩石 K＜0．001 米／日 如致密坚岩(包括沉积岩岩浆岩，变质岩)，粘土，淤泥， 泥岩 K 与岩石的空隙性质有关 与水的物理性质有关。 5． 达西定律的适用性 线性渗透定律：适用于雷诺数小于 1-10 之间某一数值的层流才服从达西定律. d v   10 = Re v为层流与紊流之间的临界流速,  为流体粘度,单位为Pa.s,流水的粘度为≈10-3Pa.s,  为 流体密度,单位为 g/cm3,d 为管径,单位为 cm; Re 的物理含义为流体的惯性力与流体粘滞 力之间的比率关系. Re 越大,即惯性力越大,愈容易出现紊流.一般 Re 2320 为紊流. 实际资料表明，自然界中的孔隙岩层、裂隙岩层以及溶穴不十分发育的岩溶岩层中的 地下水运动基本上部属层流运动。仅在溶洞发育和粗大的卵砾石岩层中才会形成局部的紊 流运动。因此，达西公式能广泛地应用于自然界中的地下水计算。可以说，达西定律是定 性分析水文地质问题和定量研究地下水运动规律的最基本定律． [课程小结]本讲讲述了地下水水头及其构成、水力梯度及其意义；重点讲述达西定律，地 下水线性流动，达西定律的适用性。 [本讲作业及要求]： (1) 请对比以下概念 渗透流速与实际流速；渗透系数与渗透率；水头与水位 （2）达西定律的应用

7asp3s,-图15水平隔水层上的潜水流在实际工件中，常需要计算地下水的天然流量。如图15所示，为一潜水含水层，由均质的砂组成，隔水底板水平，在平面上水流作平行流动。求单位过水断面的流量。dh提示：（a）I=为变数ds（b）单位过水段面的面积W=h*1=含水层厚度单位宽度渗透流量以q表示q=-Khdhds(c）求解：hi+hz hi-hzq=K.2L（3）一般情况下，可以用渗透流速除以孔隙度得到实际流速，这个实际流速与水质点的流动速度有什么联系？（4）达西定律有哪些适用条件，分析一下该定律在裂隙含水层中应用时需注意哪些问题?（5）某土柱渗流试验如下图所示，土样A和B被透水石隔开，土柱顶部水位保持恒定，当底部排水流量稳定为Q时，所测得的测压管水位H已经在图中标出，用KA和KB分别倍。表示A和B的渗透系数，则KB是KA的

在实际工件中，常需要计算地下水的天然流量。如图 15 所示，为一潜水含水层，由均质 的砂组成，隔水底板水平，在平面上水流作平行流动。求单位过水断面的流量。 提示：（a） ds dh I = − 为变数 （b）单位过水段面的面积 W=h *1=含水层厚度 单位宽度渗透流量以 q 表示 ds dh q = −Kh （c）求解： L h h h h q K 1 2 1 2 2 −  + =  （3）一般情况下，可以用渗透流速除以孔隙度得到实际流速，这个实际流速与水质点的 流动速度有什么联系？ （4） 达西定律有哪些适用条件，分析一下该定律在裂隙含水层中应用时需注意哪些问 题？ （5）某土柱渗流试验如下图所示，土样 A 和 B 被透水石隔开，土柱顶部水位保持恒定， 当底部排水流量稳定为 Q 时，所测得的测压管水位 H 已经在图中标出，用 KA 和 KB分别 表示 A 和 B 的渗透系数，则 KB是 KA 的 倍

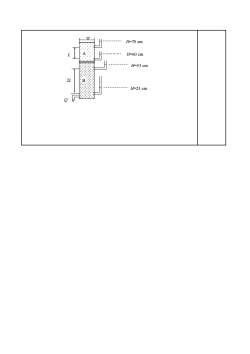
H=70 cmH=60 cmH=53cm2LH=23 cm

A B L 2L H=70 cm H=60 cm H=53 cm H=23 cm Q