《计量经济学》课程教学课件(PPT讲稿)05 多重共线性(Multicollinearity)

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 第五章 多重共线性 (Multicollinearity)
第五章 多重共线性 (Multicollinearity)

中图寒聋大些红济管挥学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 学习要点 一、 多重共线性的会义 二、多重共线性来源及对○儿SE性质的影响 三、多重共线检验:可决系数法、方差膨胀因子 四、多重共线的解决办法:逐步回归法 五、遗漏重要解释变量的后果 六、理解案例
学习要点 一、多重共线性的含义 二、多重共线性来源及对OLSE性质的影响 三、多重共线检验:可决系数法、方差膨胀因子 四、多重共线的解决办法:逐步回归法 五、遗漏重要解释变量的后果 六、理解案例

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 一、多重共线性的会义 1.以二元线性回归模型解释多重共线会义 ◆满他湿:风2好8 )(1) (2) (1)减(2:y-7=B(X1-1))+B2(X2-X2)+4-u 令y=y-了,x1=X-X,X2=X2-2 得:y,=Bx1+By,2+4,-五(=1,2,n) X11 X12 X21 X22 =(x x2)
一、多重共线性的含义 ( 1,2,., ) Y = 0 + 1 X1 + 2 X2 +u i = n ( 1,2,., ) yi = 1 xi1 + 2 yi2 +ui −u i = n 1. 以二元线性回归模型解释多重共线含义 ( 1,2,., ) Yi = 0 + 1 Xi1 + 2 Xi2 +ui i = n i 1 1 1 i 2 2 2 令 yi = Yi −Y , x = Xi − X , x = Xi − X ( ) , 1 2 1 2 21 22 11 12 x x x x x x x x x n n = = (1) (2) (1)减(2): Yi −Y = 1 (Xi1 − X1 ) + 2 (Xi2 − X2 ) + ui −u 得: ◆简化模型:

中虚寒靠大季红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL ◆多重共线性分析涉及到的相关计算: 1)xx= 2)R(x)=2 3)x=∑xx号-(∑xx)2=D ∑x∑五 简单相关系数 50)-
( ) = = = 2 1 2 2 1 2 2 1 2 1 2 2 1 1 1 2 1 2 2 1 1) x x x x x x x x x x x x x x x x x x x x = 2 2 2 1 1 2 4) x x x x r 简单相关系数 − − = − 2 1 2 1 1 2 2 1 1 2 5) ( ) x x x x x x D x x 2) R(x) = 2 3) ( ) D 2 1 2 2 2 2 x x =x1 x − x x = ◆多重共线性分析涉及到的相关计算:

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 2.多重共线的三种情况 (1)完全共线的情形 x2=ax1∑xx=a∑x,∑x号=a2∑x ww2器器x0副 2)R(x'x)=1 3)x'x=0 a∑x好 4)r= ∑xx a∑x好 =±1 V∑∑好a∑∑采a∑网 5)(x'x)1不存在
(1)完全共线的情形 2 ax1 x = , 2 1 2 2 2 2 x1 x2 = ax1 x = a x = = = 2 2 2 1 1 2 2 1 2 1 2 1 2 1 2 2 1 2 2 1 1 1) a a a x a x a x x a x x x x x x x x x 2) R(x x) =1 3) x x = 0 4) 1 2 1 2 1 2 1 2 1 2 2 1 2 2 2 1 1 2 = = = = a x a x a x x a x x x x x r 5) (x x) −1 不存在 2.多重共线的三种情况

中面寒靠大琴红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL (2)正交的情形:xx2=0,即∑xx2=0 v[图】 2)R(x'x)=2 3)x'x=∑x2∑x号 4)r= ∑x =0 ∑∑好 5)(xx)1=
(2)正交的情形: x1 x2 = 0, 即x1 x2 = 0 = = 2 2 2 1 2 1 2 2 1 2 2 1 0 0 1) x x x x x x x x x x 2) R(x x) = 2 = 2 2 2 1 3) x x x x 4) 0 2 2 2 1 1 2 = = x x x x r = − 2 2 2 1 1 1 1 5) ( ) x x x x

中面奥靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL (3)多重共线的情形 x2=ax,+y,v满足关于残差项的基本假设。 设 y越小,多重共线性越强:V越大,多重共线性越弱。 ∑xx,=∑x(a+)=a∑x,∑x号=∑(a+2=a2∑x+∑y2 川3 1 2)Rx'x)=2 3)xx=a2(∑x2)2+∑x∑y2-a2(∑x)2=∑∑2
(3)多重共线的情形 越小,多重共线性越强; 越大,多重共线性越弱。 设 满足关于残差项的基本假设。 v , 2 1 v x = ax + v v = + = = + = + 2 2 1 2 2 1 2 2 2 1 2 1 1 1 x x x (ax v) a x , x (ax v) a x v + = + = = 2 1 2 2 2 1 2 2 1 2 2 1 2 1 2 1 2 1 2 2 1 2 2 1 1 1) x v a a a x a x a x v x a x x x x x x x x x = + − = = 2 2 1 2 2 1 2 2 2 1 2 2 1 2 3) ( ) ( ) 2) R 2 x x a x x v a x x v (x x )
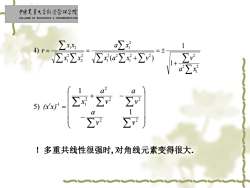
中匣寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 4)r= ∑ a 5)x= !多重共线性很强时,对角线元素变得很大
+ = + = = 2 1 2 2 2 2 1 2 2 1 2 1 2 2 2 1 1 2 1 1 ( ) 4) a x x a x v v a x x x x x r − + − = 2 2 2 2 2 2 1 1 1 1 5) v v a v a v a x (x x )- !多重共线性很强时, 对角线元素变得很大
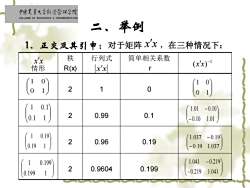
中面史靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 二、举例 1、正交及其引中:对于矩阵xx,在三种情况下: x 秩 行列式 简单相关系数 情形 R() xxl (xx) r 0 1 2 1 0 (1 0.1 1.01-0.10 0.1 1 2 0.99 0.1 -0.101.01 1 0.19 1.037-0.19 0.191 2 0.96 0.19 -0.191.037 1 0.199 1.041 -0.219 2 0.9604 0.199 0.199 -0.219 1.041
二、举例 x x 0 1 1 0 情形 秩 R(x) 行列式 简单相关系数 r 2 1 0 2 0.99 0.1 2 0.96 0.19 2 0.9604 0.199 1、正交及其引申:对于矩阵 ,在三种情况下: x x 1 ( ) − x x 0 1 1 0 0.1 1 1 0.1 0.19 1 1 0.19 0.199 1 1 0.199 − − 0.10 1.01 1.01 0.10 − − 0.19 1.037 1.037 0.19 − − 0.219 1.041 1.041 0.219 x x
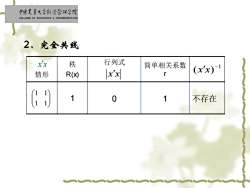
中虚寒靠大季红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 2、完全共线 xx 秩 行列式 简单相关系数 情形 R(x) xx r (xx)-1 1 0 1 不存在
2、完全共线 1 1 1 1 情形 秩 R(x) 行列式 简单相关系数 r 1 0 1 不存在 x x 1 ( ) − x x x x
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《计量经济学》课程教学课件(PPT讲稿)01 计量经济学基本问题.ppt
- 《计量经济学》课程教学课件(PPT讲稿)04 K元线性回归模型.ppt
- 《计量经济学》课程教学课件(PPT讲稿)03 矩阵代数复习.ppt
- 《计量经济学》课程教学资源(试卷习题)第十章 随机时间序列(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第八章 线性回归模型扩展(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第九章 滞后变量模型(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第六章 自相关(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第二章 简单线性回归模型(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第五章 异方差(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第七章 随机解释变量(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第四章 多重共线性(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第三章 K元线性回归模型(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第一章 计量经济学的基本问题(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)2007-2008年春A卷答案.doc
- 《计量经济学》课程教学资源(试卷习题)2007-2008年春A卷试题.doc
- 《计量经济学》课程教学资源(教案)11 联立方程模型识别和估计.doc
- 《计量经济学》课程教学资源(教案)10 滞后变量模型.doc
- 《计量经济学》课程教学资源(教案)09 K元线性回归模型扩展.doc
- 《计量经济学》课程教学资源(教案)06 广义最小二乘法(GLS)与异方差.doc
- 《计量经济学》课程教学资源(教案)08 随机解释变量.doc
- 《计量经济学》课程教学课件(PPT讲稿)02 简单线性回归模型.ppt
- 《计量经济学》课程教学课件(PPT讲稿)06 广义最小二乘法(GLS)与异方差(Heteroskedasticity).ppt
- 《计量经济学》课程教学课件(PPT讲稿)08 随机解释变量.ppt
- 《计量经济学》课程教学课件(PPT讲稿)09 K元线性回归模型的扩展.ppt
- 《计量经济学》课程教学课件(PPT讲稿)11 联立方程模型的识别和估计.ppt
- 《计量经济学》课程教学课件(PPT讲稿)10 滞后变量模型.ppt
- 《计量经济学》课程教学课件(PPT讲稿)07 自相关(Autocorrelation).ppt
- 《计量经济学》课程教学课件(PPT讲稿)12 时间序列计量经济模型.ppt
- 《国际期货市场运作》课程教学大纲 International Futures Market Operation.doc
- 《国际期货市场运作》课程授课教案(讲义,英文版).doc
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 1 The Journey Ahead.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 0 International Futures Markets Operation.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 2 Beginning with the Basics.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 3 The Modern Futures Exchange.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 7 Hedging with Spreads.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 6 Getting Started in Trading Futures.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 5 The Variety of Futures Markets.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 4 Life on the Trading Floor.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 10 Technical Analysis Chart Patterns.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 11 Timing Indicators.ppt
