《计量经济学》课程教学课件(PPT讲稿)04 K元线性回归模型

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 第四章 K元线性回归模型
第四章 K 元线性回归模型

中面寒笔大学红济管捏学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 学习要点 一、 K元线性回归模型与一元线性回归模型的区别 二、关于模型的基本假设 三、k元线性回归模型的估计、检验和应用 四、理解OLSE的优良性质 五、比较○LS法与ML法的异同和适用性 六、如何综合评价经济计量建模的效果
学习要点 一、K元线性回归模型与一元线性回归模型的区别 二、关于模型的基本假设 三、k元线性回归模型的估计、检验和应用 四、理解OLSE的优良性质 五、比较OLS法与ML法的异同和适用性 六、如何综合评价经济计量建模的效果

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 、K元线性回归模型设定 1.问题的提出 许多实际问题中,所涉及的研究对象可能受到2个以 上解释变量的影响。例如: (1)某商品的需求量与该商品的价格、消费者可支配 收入、替代品的价格等有关: (2)粮食产出受到化肥、农业机械、土地、农作物播 种面积、劳动投入、农业用电、国家财政支农支出等因素 影响。 (3)劳动者的工资受到工龄、受教育程度、所在行业、 所在地区等因素影响
1. 问题的提出 许多实际问题中,所涉及的研究对象可能受到2个以 上解释变量的影响。例如: (1)某商品的需求量与该商品的价格、消费者可支配 收入、替代品的价格等有关; (2)粮食产出受到化肥、农业机械、土地、农作物播 种面积、劳动投入、农业用电、国家财政支农支出等因素 影响。 (3)劳动者的工资受到工龄、受教育程度、所在行业、 所在地区等因素影响。 一、K元线性回归模型设定

中匣寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 2.K元线性回归模型的基本形式 总体回归模型:令X,。=1 y=BX0+BX+BX2+.+PXk+4,(i=1,2,n) 矩阵形式: Y=XB+u Y=XB 样本回归模型: y,=bX0+bX1+b2X2+.+bkX+e,(i=1,2,n) 矩阵形式: Y=Xb+e,Y=XbY-氵=e
2. K元线性回归模型的基本形式 总体回归模型:令 矩阵形式: 样本回归模型: (i 1,2,.n) 0 0 1 1 2 2 = + + + + + i = i i i i k i k Y X X X X u Y X u = + . (i 1,2,.,n) = 0 0 + 1 1 + 2 2 + + + i = i i i i k i k Y b X b X b X b X e Y = Xb + e Y = Xb ˆ , 矩阵形式: Y −Y = e ˆ Y ˆ = X 1 Xi0 =
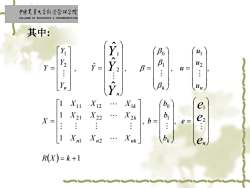
中面史靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 其中: Y- 7巧. Bo 氵= B= 川. u= Yn Y Bk un 1 X11 X12 Xik bo e 1 Y- X21 X22 X2k b b= e= : 1 Xm Xn2 e R(X)=k+1
其中: ( ) 1 , , 1 1 1 , , , ˆ , 2 1 1 0 1 2 2 1 2 2 2 1 1 1 2 1 2 1 1 0 2 1 2 1 ˆ ˆ ˆ = + = = = = = = = R X k e b b b b X X X X X X X X X X u u u Y u Y Y Y Y e e e Y Y Y n n n n k k k k k n n n

中慢寒革大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 二、 关于模型的基本假设 1、关于解释变量: (1)X1,X2,Xk是确定性变量; (2)若X是随机变量,则应满足: Cov(u;,X)=0 (3)X为满列秩矩阵, R()=k+1(其中k为解释变量个数)
二、关于模型的基本假设 1、关于解释变量: (1)x1,x2,.xk 是确定性变量; (2)若X是随机变量,则应满足: (3)X为满列秩矩阵, Cov u X ( , ) 0 i i = R X k k ( ) 1( ) = + 其中 为解释变量个数

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 2、关于随机误差 (1)服从正态分布:u~N(0,o2I) (2)等方差Var(Y)=E(Y-E(Y)2 E(XB+u-XB)2 =F(u)2 =o1 (3)无自相关Cov(4,u)=0 (,i,j=1,2,.,n)
2、关于随机误差 ~ (0, ) 2 u N I u (1) 服从正态分布: (2) 等方差 (3) 无自相关 (i≠j, i,j=1,2,.,n) Cov u u ( , ) 0 i j = 2 Var(Y) = E(Y − E(Y)) 2 = E(X + u − X) 2 = E(u) I u 2 =

中慢寒靠大学红济管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 三、k元线性回归模型的估计 1、模型的OLS估计 ∑y-2-2e-(eeen) =ee en =(Y-)Y- =(Y-Xb)(Y-Xb) =YY-YX6-b'XY+b'XXD =YY-26XY+bXX6 =f(b)
三、k元线性回归模型的估计 1、模型的OLS估计 = = − = n i i n i i i Y Y e 1 2 1 2 ) ˆ ( ( ) = n n e e e e e e 2 1 1 2 = e e ) ˆ ) ( ˆ = (Y −Y Y −Y = (Y − Xb)(Y − Xb) = YY −YXb−bXY +bXXb = YY − 2bXY +bXXb = f (b)

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 就fb)对b求一次偏导,令其为零, 0b=0 ab 得:-2XY+2XXb=0 则b的估计式:b=(XX)XY 就fb)对b求二次偏导,得 0他=2XXy=2XX (正定二次型) 0b2 说明得到的b可以使得】 E(Y-1) 2达到最小
0 ( ) = b f b -1 则b的估计式: b=(X'X) X'Y 就 f (b) 对b 求一次偏导,令其为零, X X X X b f b = = (2 ) 2 2 2 ( ) (正定二次型) 说明得到的b可以使得 = = − = n i i n i i i Y Y e 1 2 1 2 ) ˆ ( 达到最小。 就 f (b) 对b 求二次偏导,得 得: −2XY +2XXb = 0

中面寒笔大学红济管捏学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 2、最小二乘估计量(OLSE)的性质 (1)线性性 b是的线性组合 b=[(XX)X]Y b是u的线性组合 b=(XX)X(XB+u) =B+(XX)Xu (2)无偏性 E(b)=E[(X'X)X(XB+u)] =E[B+(XX)X'u] =B+(XX)XE(u) =B
2、最小二乘估计量(OLSE)的性质 (1) 线性性 b是Y的线性组合 b是u的线性组合 -1 b= (X'X) X' Y -1 -1 b=(X'X) X'(X +u) = +(X'X) X'u (2) 无偏性 -1 -1 -1 E(b)=E[(X'X) X'(X +u) ] =E[ +(X'X) X'u] = +(X'X) X'E(u) =
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《计量经济学》课程教学课件(PPT讲稿)03 矩阵代数复习.ppt
- 《计量经济学》课程教学资源(试卷习题)第十章 随机时间序列(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第八章 线性回归模型扩展(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第九章 滞后变量模型(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第六章 自相关(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第二章 简单线性回归模型(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第五章 异方差(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第七章 随机解释变量(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第四章 多重共线性(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第三章 K元线性回归模型(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第一章 计量经济学的基本问题(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)2007-2008年春A卷答案.doc
- 《计量经济学》课程教学资源(试卷习题)2007-2008年春A卷试题.doc
- 《计量经济学》课程教学资源(教案)11 联立方程模型识别和估计.doc
- 《计量经济学》课程教学资源(教案)10 滞后变量模型.doc
- 《计量经济学》课程教学资源(教案)09 K元线性回归模型扩展.doc
- 《计量经济学》课程教学资源(教案)06 广义最小二乘法(GLS)与异方差.doc
- 《计量经济学》课程教学资源(教案)08 随机解释变量.doc
- 《计量经济学》课程教学资源(教案)07 自相关.doc
- 《计量经济学》课程教学资源(教案)05 多重共线性.doc
- 《计量经济学》课程教学课件(PPT讲稿)01 计量经济学基本问题.ppt
- 《计量经济学》课程教学课件(PPT讲稿)05 多重共线性(Multicollinearity).ppt
- 《计量经济学》课程教学课件(PPT讲稿)02 简单线性回归模型.ppt
- 《计量经济学》课程教学课件(PPT讲稿)06 广义最小二乘法(GLS)与异方差(Heteroskedasticity).ppt
- 《计量经济学》课程教学课件(PPT讲稿)08 随机解释变量.ppt
- 《计量经济学》课程教学课件(PPT讲稿)09 K元线性回归模型的扩展.ppt
- 《计量经济学》课程教学课件(PPT讲稿)11 联立方程模型的识别和估计.ppt
- 《计量经济学》课程教学课件(PPT讲稿)10 滞后变量模型.ppt
- 《计量经济学》课程教学课件(PPT讲稿)07 自相关(Autocorrelation).ppt
- 《计量经济学》课程教学课件(PPT讲稿)12 时间序列计量经济模型.ppt
- 《国际期货市场运作》课程教学大纲 International Futures Market Operation.doc
- 《国际期货市场运作》课程授课教案(讲义,英文版).doc
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 1 The Journey Ahead.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 0 International Futures Markets Operation.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 2 Beginning with the Basics.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 3 The Modern Futures Exchange.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 7 Hedging with Spreads.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 6 Getting Started in Trading Futures.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 5 The Variety of Futures Markets.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 4 Life on the Trading Floor.ppt
