《计量经济学》课程教学资源（试卷习题）第五章 异方差（含答案）

第五章异方差 一、填空题 1.以 数据为样本建立起来的计量经济模型中的随机误差项往往存在 ,表示为 2.在存在异方差情况下，普通最小二乘法(0LS)估计量仍是无偏但不再 ，通 常使用的t检验和检验是无效的。 3.在存在异方差情况下，常用的0LS法可能是高估也可能是低估了估计量的 4.在应用工作中，异方差究竟与哪个或娜些解释变量有关往往是未知的，需要尝试构造残 差序列，与可能导致异方差的解释变量之间的回归模型，根据来确定。 5.利用格菜泽检验(Glejser test)进行异方差的检验，可以达到两个目的 .和 6.异方差的检验方法有多种，很难说哪种方法是最好的，但有一个共同的思路，就是 7.Goldfeld-一Quandt检验用于检验递增（或递减）即单调变化的 8. 法是解决模型异方差的有效方法之一。 二、选择题 1.产生异方差性的主要原因是( A模型中省略了某些重要变量；B模型设定误差： C测量误差的变化； D.截面数据中总体各单位的差异。 2.异方差性的检验方法有

第五章 异方差 一、填空题 1. 以 数据为样本建立起来的计量经济模型中的随机误差项往往存在 _，表示为 。 2. 在存在异方差情况下，普通最小二乘法（OLS）估计量仍是无偏但不再 ，通 常使用的 t 检验和 检验是无效的。 3. 在存在异方差情况下，常用的 OLS 法可能是高估也可能是低估了估计量的 。 4.在应用工作中，异方差究竟与哪个或哪些解释变量有关往往是未知的，需要尝试构造残 差序列 i e 与可能导致异方差的解释变量之间的回归模型，根据 来确定。 5. 利用格莱泽检验（Glejser test）进行异方差的检验，可以达到两个目的： 和 。 6. 异方差的检验方法有多种，很难说哪种方法是最好的，但有一个共同的思路，就是 _。 7. Goldfeld—Quandt 检验用于检验递增（或递减）即单调变化的 。 8. 法是解决模型异方差的有效方法之一。 二、选择题 1．产生异方差性的主要原因是（ ） A.模型中省略了某些重要变量； B.模型设定误差； C.测量误差的变化； D.截面数据中总体各单位的差异。 2.异方差性的检验方法有( )

A图示检验法 B格莱泽检验 C.怀特(White)检验 D.回归检验法 E.DW检验 F.Goldfeld-Quandt test(G-Q检验) G.ARCH检验 3.Goldfeld-Quandt检验法的过程做法是( A.模型除了存在异方差问题外，其它假定条件均满足 B,样本容量尽可能大 C.将与异方差相关的某解释变量按其观测值的大小顺序排列 D.随机误差项服从正态分布、零期望、无自相关 E.将排列在中间的约14的观测值删除掉，形成两个子样本 F.构造F统计量，判断异方差是否存在 4.针对存在异方差现象的模型进行估计，下面哪些方法可能是适用的( A.加权最小二乘法 B.工具变量法 C.广义差分法 D.广义最小二乘法E普通最小二乘法 三、问答题 1简述异方差性的含义. 2.简述异方差性的后果 3.列举异方差性的检验方法。 4.检验计量经济模型是否存在异方差，可以用布罗歇一帕甘检验(Breusch Pagan)和怀 特(White)检验，请说明这二种检验的差异和适用性 5简述异方差检验方法的共同思路。 6.列举异方差的解决办法，】 7.对变量取对数通常能降低异方差性，但须对这种模型的随机误差项的性质给予足

A.图示检验法 B.格莱泽检验 C.怀特(White)检验 D.回归检验法 E.DW 检验 F. Goldfeld-Quandt test(G-Q 检验) G. ARCH 检验 3.Goldfeld-Quandt 检验法的过程做法是（ ） A．模型除了存在异方差问题外，其它假定条件均满足 B．样本容量尽可能大 C．将与异方差相关的某解释变量按其观测值的大小顺序排列 D. 随机误差项服从正态分布、零期望、无自相关 E. 将排列在中间的约1/4的观测值删除掉, 形成两个子样本 F. 构造F统计量，判断异方差是否存在 4. 针对存在异方差现象的模型进行估计，下面哪些方法可能是适用的（ ）。 A. 加权最小二乘法 B. 工具变量法 C. 广义差分法 D. 广义最小二乘法 E. 普通最小二乘法 三、问答题 1.简述异方差性的含义。 2.简述异方差性的后果。 3.列举异方差性的检验方法。 4.检验计量经济模型是否存在异方差，可以用布罗歇—帕甘检验（Breusch Pagan）和怀 特（White）检验，请说明这二种检验的差异和适用性。 5.简述异方差检验方法的共同思路。 6.列举异方差的解决办法。 7. 对变量取对数通常能降低异方差性，但须对这种模型的随机误差项的性质给予足

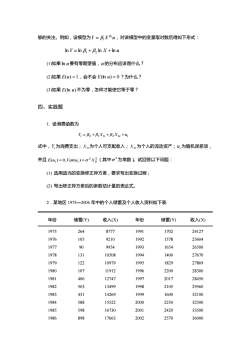
够的关注.例如，设模型为Y=RX一“，对该模型中的变量取对数后得如下形式 (1)如果nu要有零期望值，u的分布应该是什么？ 2如果E()=1,会不会E)=0?为什么 (3如果E0)不为零，怎样才能使它等于零 四、实践题 1.设消费函数为 Y,=+月Xw+BX+4 式中，Y为消费支出；X,为个人可支配收入X为个人的流动资产；4，为随机误差项 并且E(u,)=0,Vam(u,)=o2X2（其中σ2为常数b试回答以下问题 ()选用适当的变换修正异方差，要求写出变换过程 (2)写出修正异方差后的参数估计量的表达式。 2.某地区1975一2006年中的个人储蓄及个人收入资料如下表 年份 储蓄(Y) 收入(X) 年份 储蓄()收入（凶 1975 264 877m 1991 1702 24127 1976 105 9210 19 1578 25604 01 。 94 2 27670 12 1097 27869 11912 畅0机 12747 9 29560 16730 176 2570

够的关注。例如，设模型为 Y X u 2 1  =  ，对该模型中的变量取对数后得如下形式： ln Y = ln 1 + 2 ln X + ln u (1)如果 ln u 要有零期望值， u 的分布应该是什么？ (2)如果 E(u) =1 ，会不会 E(ln u) = 0 ？为什么？ (3)如果 E(ln u) 不为零，怎样才能使它等于零？ 四、实践题 1. 设消费函数为 Yi =  0 + 1X1i +  2 X2i +ui 式中， Yi 为消费支出； X1i 为个人可支配收入； X 2i 为个人的流动资产； i u 为随机误差项， 并且 2 1 2 ( ) 0, ( ) E ui = Var ui = X i （其中 2  为常数）。试回答以下问题： (1) 选用适当的变换修正异方差，要求写出变换过程； (2) 写出修正异方差后的参数估计量的表达式。 2．某地区 1975—2006 年中的个人储蓄及个人收入资料如下表: 年份 储蓄(Y) 收入(X) 年份 储蓄(Y) 收入(X) 1975 264 8777 1991 1702 24127 1976 105 9210 1992 1578 25604 1977 90 9954 1993 1654 26500 1978 131 10508 1994 1400 27670 1979 122 10979 1995 1829 27869 1980 107 11912 1996 2200 28300 1981 406 12747 1997 2017 28450 1982 503 13499 1998 2105 29560 1983 431 14269 1999 1600 32100 1984 588 15522 2000 2250 32500 1985 598 16730 2001 2420 33500 1986 898 17663 2002 2570 36000

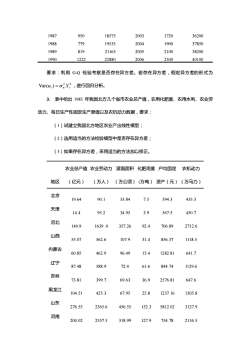
950 18575 2003 1720 36200 198 779 19535 204 190l 37850 21163 2005 2100 38200 1222 22880 2006 2300 40100 要求：利用GQ检验考察是否存在异方差。若存在异方差，假定异方差的形式为 Var(u,)=oX,进行回归分析 3.表中给出1985年我国北方几个省市农业总产值，农用化肥量、农用水利、农业劳 动力、每日生产性固定生产原值以及农机动力数据，要求 (1)试建立我国北方地区农业产出线性模型， (2)选用适当的方法检验模型中是否存在异方差： (3)如果存在异方差，采用适当的方法加以修正。 农业总产值农业劳动力灌溉面积化肥用量户均固定 农机动力 地区 (亿元) (万人)》 (万公顷)（万吨） 资产（元） (万马力)》 19.64 90.1 33.84 7.5 394.3 435.3 天津 只g 95.2 34.95 3.9 567. 450.7 河北 149.9 1639.0 357.26 92.4 706.89 2712.6 山西 55.07 562.6 107.9 31.4 856.37 1118.5 内蒙古 60 85 154 1282.81 641.7 辽宁 7.4 844.74 129.6 吉林 2576.8 647.6 黑龙 237 1305.8 山东 3127g 200.02 2557. 318.99 127.9 754.78 2134

1987 950 18575 2003 1720 36200 1988 779 19535 2004 1900 37850 1989 819 21163 2005 2100 38200 1990 1222 22880 2006 2300 40100 要求：利用 G-Q 检验考察是否存在异方差。若存在异方差，假定异方差的形式为 2 2 Var( ) ui =  u Xi ，进行回归分析。 3. 表中给出 1985 年我国北方几个省市农业总产值，农用化肥量、农用水利、农业劳 动力、每日生产性固定生产原值以及农机动力数据，要求： （1）试建立我国北方地区农业产出线性模型； （2）选用适当的方法检验模型中是否存在异方差； （3）如果存在异方差，采用适当的方法加以修正。 地区 农业总产值 农业劳动力 灌溉面积 化肥用量 户均固定 农机动力 （亿元） （万人） （万公顷） (万吨） 资产（元） （万马力） 北京 19.64 90.1 33.84 7.5 394.3 435.3 天津 14.4 95.2 34.95 3.9 567.5 450.7 河北 149.9 1639 .0 357.26 92.4 706.89 2712.6 山西 55.07 562.6 107.9 31.4 856.37 1118.5 内蒙古 60.85 462.9 96.49 15.4 1282.81 641.7 辽宁 87.48 588.9 72.4 61.6 844.74 1129.6 吉林 73.81 399.7 69.63 36.9 2576.81 647.6 黑龙江 104.51 425.3 67.95 25.8 1237.16 1305.8 山东 276.55 2365.6 456.55 152.3 5812.02 3127.9 河南 200.02 2557.5 318.99 127.9 754.78 2134.5

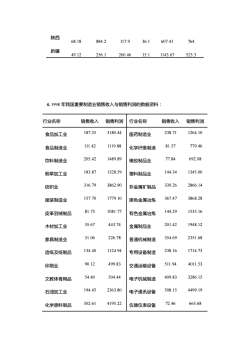
陕西 68.18 884.2 117.9 36.1 607.41 764 新疆 49.12 256.1 260.4615.11143.67523.3 4.1998年我国重要制造业销售收入与销售利润的数据资料 行业名称 销售收入销售利润 行业名称 销售收入销售利润 食品加工业 187.25 3180.44 医药制造业 238.71 1264.10 食品制造业 111.42 1119.88 化学纤维制造 81.57 779.46 饮料制造业 205.42 1489.89 橡胶制品业 77.84 692.08 烟草加工业 183.87 1328.59 望料制品业 144.34 1345.00 纺织业 316.79 3862.90 非金属矿制品 39,26 2866.14 服装制造业 157.70 1779.10 黑色金属治炼 367.47 3868.28 皮革羽绒制品 81.73 1081.77 有色金属治炼 144.29 1535.16 木材加工业 35.67 443.74 金属制品业 201.42 1948.12 家具制造业 31.06 226.78 普通机械制造 354.69 2351.68 造纸及纸制品 134.40 124.94 专用设备制造 238.16 1714.73 印刷业 90.12 499.83 交通运输设备 511.94 4011.53 文教体育用品 54.40 504.44 电子机械制造 409.83 3286.15 石油加工业 194.45 2363.80 电子通讯设备 508.15 499.19 化学原料制品 502.61 4195.22 仪器仪表设备 72.46 663.68

陕西 68.18 884.2 117.9 36.1 607.41 764 新疆 49.12 256.1 260.46 15.1 1143.67 523.3 4. 1998 年我国重要制造业销售收入与销售利润的数据资料： 行业名称 销售收入 销售利润 行业名称 销售收入 销售利润 食品加工业 187.25 3180.44 医药制造业 238.71 1264.10 食品制造业 111.42 1119.88 化学纤维制造 81.57 779.46 饮料制造业 205.42 1489.89 橡胶制品业 77.84 692.08 烟草加工业 183.87 1328.59 塑料制品业 144.34 1345.00 纺织业 316.79 3862.90 非金属矿制品 339.26 2866.14 服装制造业 157.70 1779.10 黑色金属冶炼 367.47 3868.28 皮革羽绒制品 81.73 1081.77 有色金属冶炼 144.29 1535.16 木材加工业 35.67 443.74 金属制品业 201.42 1948.12 家具制造业 31.06 226.78 普通机械制造 354.69 2351.68 造纸及纸制品 134.40 1124.94 专用设备制造 238.16 1714.73 印刷业 90.12 499.83 交通运输设备 511.94 4011.53 文教体育用品 54.40 504.44 电子机械制造 409.83 3286.15 石油加工业 194.45 2363.80 电子通讯设备 508.15 4499.19 化学原料制品 502.61 4195.22 仪器仪表设备 72.46 663.68

试完成以下问题 ()求销售利润与销售收入的样本回归函数，并对模型进行经济意义检验和统计检验； (2)分别用图形法、Glejser方法、White方法检验模型是否存在异方差： (3)如果模型存在异方差，选用适当的方法对异方差性进行修正，。 5.表中给出1969年20个国家的股票价格(Y)和消费者价格年百分率变化(X)的- 个横截面数据。 股票价格变化率% 消费者价格变化率% 国家 1澳大利亚 4.3 2奥地利 3.比利时 24 4加拿大 9 24 5智利 25.5 26.4 6.丹麦 p 7芬兰 5.5 8法国 99 9,德国 133 22 10.印度 , g 1爱尔兰 64 4 12以色列 中p 13意大利 3.3 14日本 135

试完成以下问题: (1) 求销售利润与销售收入的样本回归函数，并对模型进行经济意义检验和统计检验； (2) 分别用图形法、Glejser 方法、White 方法检验模型是否存在异方差； (3) 如果模型存在异方差，选用适当的方法对异方差性进行修正。 5. 表中给出 1969 年 20 个国家的股票价格（Y）和消费者价格年百分率变化（X）的一 个横截面数据。 国家 股票价格变化率% Y 消费者价格变化率% X 1.澳大利亚 5 4.3 2.奥地利 11.1 4.6 3.比利时 3.2 2.4 4.加拿大 7.9 2.4 5.智利 25.5 26.4 6.丹麦 3.8 4.2 7.芬兰 11.1 5.5 8.法国 9.9 4.7 9.德国 13.3 2.2 10.印度 1.5 4 11.爱尔兰 6.4 4 12.以色列 8.9 8.4 13.意大利 8.1 3.3 14.日本 13.5 4.7

15.墨西哥 4.7 5.2 16.荷兰 7.5 3.6 17新西兰 4.7 3.6 18瑞典 19.英国 7.5 3.9 20.美国 9 , 试根据资料完成以下问题 (1)将Y对X回归并分析回归中的残差： (2)因智利的数据出现了异常，去掉智利数据后，重新作回归并再次分析回归中的残 差 (3)如果根据第1条的结果你将得到有异方差性的结论，而根据第2条的结论你又得 到相反的结论，对此你能得出什么样的结论？ 参考答案 一、填空题 1.横截面，异方差，au)=oX,):2.有效；F,3.统计检验结果。4.标准差。5。 检验异方差的存在性、获得异方差的形式：6.检验残差项的方差与解释变量观察值之间的 相关性。7.异方差。8广义最小二乘法G1$) 二、选择题 1.ABCD;2.ABCFG;3.ABCDEF;4.AD 三、问答题 1.答：对于模型

15.墨西哥 4.7 5.2 16.荷兰 7.5 3.6 17.新西兰 4.7 3.6 18.瑞典 8 4 19.英国 7.5 3.9 20.美国 9 2.1 试根据资料完成以下问题: (1) 将 Y 对 X 回归并分析回归中的残差； (2) 因智利的数据出现了异常，去掉智利数据后，重新作回归并再次分析回归中的残 差； (3) 如果根据第 1 条的结果你将得到有异方差性的结论，而根据第 2 条的结论你又得 到相反的结论，对此你能得出什么样的结论？ 参考答案 一、填空题 1. 横截面，异方差， ( ) ( ) 2 i u Xi Var u = f ；2.有效；F。3. 统计检验结果。 4. 标准差。5. 检验异方差的存在性、获得异方差的形式；6. 检验残差项的方差与解释变量观察值之间的 相关性。7.异方差。8. 广义最小二乘法(GLS) 二、选择题 1.ABCD; 2. ABCFG; 3.ABCDEF; 4.AD 三、问答题 1. 答：对于模型

y,=B。+BnXn+BX2+.+BXk+u,i-l.2n 同方差性假设为：Var(u,)=o2=常数，1-1,2.，n 如果出现：Var(,)=of(X)i=l.2n 即对于不同的样本值，随机扰动项的方差不再是常数，而是互不相同的，即 Vamu,)=c2≠常数(i-1,2,m)）,称为随机扰动项异方差。 2,答：（1)参数估计量仍然具有无偏性，但非有效，在大样本情况下仍不具有一致性。 (2)变量的显著性检验失去意义， （3)模型的预测失效。 3.答：主要有图示检验法、格菜泽检验、戈德菲尔特一夸特检验(G-Qt)、布罗歇 一帕甘检验(Breusch Pagan)、怀特(White)检验法等等。 国示法。异方差是指：，的方差随解释变量的变化而变化。可以利用YX的散点图，或 者残差平方与X的散点图来近似判断称为图示法。图示检验法只能进行大概的判断，其 他检验方法更为严格。常用的是格莱泽检验。 格莱泽检验。该法以，为被解释变量，以原模型的某一或多个解释变量X,为解释变量， 建立如下方程：=+X,)+6。选择关于X,的不同函数形式，对方程进行估计并进 行显著性检验，如果存在某一函数形式，使得方程显著性成立，说明原模型存在异方差。这 种方法需要反复试算 Gold-Quandt检验简称G-Q检验。将样本分为两个部分：样本(1)和样本(2)，然后 分别对样本(1)和样本(2)进行回归分析，分别求出RSS,和RSS2,用RSS,和RSS,的 比构成F统计量，进行检验，判断异方差是否存在，称为G-Q检验。该检验的前提条件为 （1)样本容量较大，(2)异方差是递增或递减型的，(3)，服从正态分布，除异方差之 外，满足其他假设条件

Yi =  0 + 1Xi1 +  2Xi2 ++  k Xik + ui ， i=1,2,.,n 同方差性假设为： Var(ui ) =  u 2 = 常数， i=1,2,.,n 如果出现： ( ) ( ) 2 i u Xi Var u =  f ， i=1,2,.,n 即对于不同的样本值，随机扰动项的方差不再是常数，而是互不相同的。即 =  2 ( ) ui Var ui  常数（ i = 1,2,., n)，称为随机扰动项异方差。 2．答：（1）参数估计量仍然具有无偏性，但非有效，在大样本情况下仍不具有一致性。 （2）变量的显著性检验失去意义。 （3）模型的预测失效。 3．答：主要有图示检验法、格莱泽检验、戈德菲尔特—夸特检验（G-Q test）、布罗歇 —帕甘检验（Breusch Pagan）、怀特（White）检验法等等。 图示法。异方差是指 i e 的方差随解释变量的变化而变化。可以利用 Y-X 的散点图，或 者残差平方 2 i e 与 X 的散点图来近似判断称为图示法。图示检验法只能进行大概的判断，其 他检验方法更为严格。常用的是格莱泽检验。 格莱泽检验。该法以 i e 为被解释变量，以原模型的某一或多个解释变量 X i 为解释变量， 建立如下方程： = + ( ) + i 0 1 Xi e b b f 。选择关于 X i 的不同函数形式，对方程进行估计并进 行显著性检验，如果存在某一函数形式，使得方程显著性成立，说明原模型存在异方差。这 种方法需要反复试算。 Gold-Quandt 检验简称 G-Q 检验。将样本分为两个部分：样本（1）和样本（2），然后 分别对样本（1）和样本（2）进行回归分析，分别求出 RSS1 和 RSS2 ，用 RSS1 和 RSS2 的 比构成 F 统计量，进行检验，判断异方差是否存在，称为 G-Q 检验。该检验的前提条件为； （１）样本容量较大，（２）异方差是递增或递减型的，（３） i u 服从正态分布，除异方差之 外，满足其他假设条件

布罗歇一帕甘检验(Breusch Pagan)。与G-Q法不同，该方法不要求按照误差大小对 观察对像进行排序，也不要求删掉部分观察对像，故这种方法的操作性更强。考虑横型的异 方差形式 ai=f(Z) 该函数可以取线性或排线性。变量Z是一个向量，它可以包括回归模型中的解释变量X,也 可以是X之外的其他变量。该检验的做法是，首先利用0LS法估计回归模型并得到残差序 列e,接若进行下列辅助回归： e2=a0+a1Z1+a,Z,+.+anZ。+8 该回归式的可决系数用R?表示。对该回归结果进行F检验或拉格朗日乘子(ML)检验，则 F= 1-R)m-p-) 检验异方差的M统计量为： LM=nR 该统计量渐近服从自由度为p的，分布。查相应的统计分布表，可以确定原模型残差序列 是否存在异方差。如果辅助回归式中只有一个Z,变可以利用估计结果提供的信息对异方差 进行校正。 怀特(White)检验。建立检验异方差的辅助回归模型，即e对所有解释变量及其平方 项（或加上交叉项）进行回归。举例来说，对于二元线性回归横型 Y,=B。+BX+B2X2+4, 进行回归分析后求出，可建立如下检验异方差的辅助回归模型： e,2=a+a,Xn+a2X2+a,X7+a4X2（不含交叉项) e,=4+4,Xn+aX2+a3X7+a4X2+a5XXa（含交叉项) 对其回归可得R2。 该检验的假设为 H。:不存在异方差 H,:存在异方差 检验的统计量为： m=nR2 n为样本容量，R为可决系数，m近似服从自由度为k(解释变量的个数)的x分布。查 x分布，确定是否应该接受不存在异方差的原假设。 4,答：当人们猜测异方差只取决于某些解释变量时，布罗歇一帕甘检验(Breusch Pagan)

布罗歇—帕甘检验（Breusch Pagan）。与 G-Q 法不同，该方法不要求按照误差大小对 观察对象进行排序，也不要求删掉部分观察对象，故这种方法的操作性更强。考虑模型的异 方差形式： ( ) 2 u Zi f i  = 该函数可以取线性或非线性。变量 Z 是一个向量，它可以包括回归模型中的解释变量 X，也 可以是 X 之外的其他变量。该检验的做法是，首先利用 OLS 法估计回归模型并得到残差序 列 i e ，接着进行下列辅助回归： =  + + + + +  Z Z pZ p e 2 0 1 1 2 2  该回归式的可决系数用 2 Re 表示。对该回归结果进行 F 检验或拉格朗日乘子（ML）检验，则 (1 ) /( 1) / 2 2 − − − = R n p R p F e e 检验异方差的 LM 统计量为： 2 LM = nRe 该统计量渐近服从自由度为 p 的 2  分布。查相应的统计分布表，可以确定原模型残差序列 是否存在异方差。如果辅助回归式中只有一个 Z，变可以利用估计结果提供的信息对异方差 进行校正。 怀特（White）检验。建立检验异方差的辅助回归模型，即 2 i e 对所有解释变量及其平方 项（或加上交叉项）进行回归。举例来说，对于二元线性回归模型 Yi =  0 + 1Xi1 +  2Xi2 + ui 进行回归分析后求出 2 i e ，可建立如下检验异方差的辅助回归模型： 2 4 2 2 0 1 1 2 2 3 1 2 i Xi Xi Xi Xi e = + + + + （不含交叉项） 或 5 1 2 2 4 2 2 0 1 1 2 2 3 1 2 i Xi Xi Xi Xi Xi Xi e = + + + + + （含交叉项） 对其回归可得 2 R 。 该检验的假设为： H0 ：不存在异方差 H1 ： 存在异方差 检验的统计量为： 2 m = nR n 为样本容量， 2 R 为可决系数， m 近似服从自由度为 k (解释变量的个数)的 2  分布。查 2  分布，确定是否应该接受不存在异方差的原假设。 4．答：当人们猜测异方差只取决于某些解释变量时，布罗歇—帕甘检验（Breusch Pagan）

比较适合使用；当人们猜测异方差不仅取决于某些解释变量，还取决于这些自变量的平方和 它们的交叉乘积项时，怀特(Whit心)检验比较适合使用。虽然，有时使用布罗歌一帕甘检 验无法检验出异方差的存在，但用怀特(White)检验却能检测出来。不过，怀特(White) 检验要用掉很多自由度。 5,答：由于异方差性，相对于不同的样本点，也就是相对于不同的解释变量观测值， 随机误差项具有不同的方差，那么检验异方差性，也就是检验随机误差项的方差与解释变量 观测值之间的相关性。各种检验方法就是在这个思路下发展起来的。 6.答：常用两种方法：对数法、广义最小二乘法(GLS)、加权最小二乘法(GLS)。 (1)对数法。将模型中的被解释变量和解释变量都采用对数的形式。双对数模型形式 压缩异方差的效果比较明显。 (2)广义最小二乘法。原理是，对于线性回归模型： Y=XB+u 如果残差项的方差为 Varu)=o'Q=G'PP 其中≠1，Q可以分解为PP,且P为非奇异阵，以P左乘原模型两边，得 P-Y=P-X6+P-u 即：y=XB+W 则：Vaw)=VaP-0=Ep-ap-')=o 可见以上对原模型的GLS变换消除了异方差问题。 以代数的形式表示以上异方差问题，一般地写为：au,)=E)=o/X) 用GLS法处理原模型，为 rJ

比较适合使用；当人们猜测异方差不仅取决于某些解释变量，还取决于这些自变量的平方和 它们的交叉乘积项时，怀特（White）检验比较适合使用。虽然，有时使用布罗歇—帕甘检 验无法检验出异方差的存在，但用怀特（White）检验却能检测出来。不过，怀特（White） 检验要用掉很多自由度。 5．答：由于异方差性，相对于不同的样本点，也就是相对于不同的解释变量观测值， 随机误差项具有不同的方差，那么检验异方差性，也就是检验随机误差项的方差与解释变量 观测值之间的相关性。各种检验方法就是在这个思路下发展起来的。 6．答：常用两种方法：对数法、广义最小二乘法（GLS）、加权最小二乘法（GLS）。 （1）对数法。将模型中的被解释变量和解释变量都采用对数的形式。双对数模型形式 压缩异方差的效果比较明显。 （2）广义最小二乘法。原理是，对于线性回归模型： Y = X +u 如果残差项的方差为 Var u = u = uPP 2 2 ( )   其中   I ,  可以分解为 PP , 且 P 为非奇异阵，以 −1 P 左乘原模型两边，得 P Y P X P u −1 −1 −1 =  + 即：    Y = X  + u 则： ( ) ( ) ( ) I 1 1 1 2 Var u Var P u E P uu P =u = =   − − −  可见以上对原模型的 GLS 变换消除了异方差问题。 以代数的形式表示以上异方差问题，一般地写为： ( ) ( ) ( ) 2 2 i i u Xi Var u = E u = f 用 GLS 法处理原模型，为 ( ) ( ) ( ) 1 ( ) 0 1 i i i i i i i f X u f X X f X f X Y =  +  +