《计量经济学》课程教学课件(PPT讲稿)03 矩阵代数复习

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAU 第三章 矩阵代数复习
第三章 矩阵代数复习

中面寒笔大学红济管捏学院 COLLEGE OF ECONOMICS MANAGEMENT.CA 复习要点 一、幂等阵、矩阵的迹、秩、二次型、 二、多项式的矩阵表达和求导 三、数学期望和方差协方差的矩阵表达
复习要点 一、幂等阵、矩阵的迹、秩、二次型、 二、多项式的矩阵表达和求导 三、数学期望和方差协方差的矩阵表达

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 矩阵 1、实对称幂等矩阵 令A为对称方阵,则侧A=A 如果A是幂等矩阵,则A=A2=A3=. 即A乘以本身若干次仍为A
1、实对称幂等矩阵 令A为对称方阵,则 如果A是幂等矩阵,则 A = A2 = A3 =. 即A乘以本身若干次仍为A。 一、矩阵 A = A

中面寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 2、矩阵的迹 矩阵的迹就是方阵对角线元素之和,例如方阵的迹 表示为: tr(A)=a11+a22+.+ann 对于mxn阶矩阵A和nxm阶矩阵B: tr(AB)=tr(BA) 简单地推广到 tr(ABC)=tr(BCA)=tr(CAB) 3、矩阵的秩 矩阵的秩定义为m×n阶矩阵不为零的子式的最高阶数
2、矩阵的迹 矩阵的迹就是方阵对角线元素之和,例如方阵的迹 表示为: tr(A)=a11+a22+.+ann 对于mxn阶矩阵A和nxm阶矩阵B: tr(AB)=tr(BA) 简单地推广到 tr(ABC)=tr(BCA)=tr(CAB) 3、矩阵的秩 矩阵的秩定义为m×n阶矩阵不为零的子式的最高阶数

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 二、多项式的矩阵表达和求导 1.多项式求导 X d 令 X2 a, Y= a= 。 若Y是n个自变量的函数,即 Y=f(X)=aX]+aX2+.+axn
二、多项式的矩阵表达和求导 若Y是n个自变量的函数,即 X a X a X an Xn Y = f ( ) = 1 1 + 2 2 +.+ = X n X X X 2 1 令 = n a a a a 2 1 1.多项式求导

中匣寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL Y=f(X)=aXj+aX2+.+anXn =(a1a2.an) =a'X 三种表达方式不 同而已,但矩阵形 式简练 a =(X1X2.Xn) =Xa
X a X a X an Xn Y = f ( ) = 1 1 + 2 2 +.+ ( ) a X X X X a a a n n = = 2 1 1 2 ( ) X a a a a X X X n n = = 2 1 1 2 三种表达方式不 同而已,但矩阵形 式简练
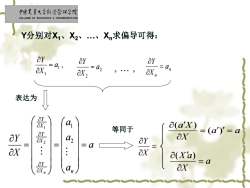
中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL Y分别对X、X2、X求偏导可得: Y =413 ay ay OX OX2 表达为 ay 41 等同于 a(a'x) ay 影 =(d')'=a 42 ay ax : =a OX Ox a(Xa) ay -a 0 OX
Y分别对X1、X2、.、Xn求偏导可得: , 1 1 a X Y = 2 2 a X Y = n n a X Y = , , a a a a X Y X n Y X Y X Y n = = = 2 1 2 1 a a X a X = = ( ) ( ) a X X a = ( ) 等同于 表达为 = X Y

中虚寒靠大季红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 2.二次型的矩阵表达和求导 例如,对于二次型:Y=f(X)=a1X+2a2XX2+a22X =X'AX 其中 X A= (x, 4a21 22 =2dX+2dnX, ay a(xAX) 2a11X1+2a412X2 OX Ox OX 2412X1+2a22X2 OY=2dX+2dnX: O =2 a21
2. 二次型的矩阵表达和求导 = 2 1 X X X = 21 22 11 12 a a a a A X A X Y f X X a X X a X ( ) a 2 2 1 2 1 2 2 2 2 2 1 1 1 = 例如, 对于二次型: = = + + 其中 11 1 12 2 1 2a X 2a X X Y = + 12 1 22 2 2 2a X 2a X X Y = + AX X X a a a a a X a X a X a X X X AX X Y 2 2 2 2 ( ) 2 2 2 1 2 1 2 2 1 1 1 2 1 2 1 2 2 2 1 1 1 1 2 2 = = + + = =

中面史靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 对于一般的二次型, Y=X'AX =ax+2a2X X2 +2aX X:+.+2ax x +a2X3+2a23X2X3+.+2a2nX2Xm +a33X3+.+2a3nX3Xm 有下列结论: ay a(XAX) 2AX OX OX 二次型的导数
n X Xn X a X X a X X a 1 2 1 2 1 3 1 3 1 1 2 1 1 1 Y = XAX = a + 2 + 2 ++ 2 n X Xn a X a X X a 2 3 2 3 2 2 2 2 2 2 + + 2 ++ 2 a X a3n X3 X n 2 + 3 3 3 ++ 2 2 + annX n AX X X AX X Y 2 ( ) = = 对于一般的二次型, 有下列结论: 二次型的导数

中匣寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL XAX=aX+2a2x X2+2a3X X3 +a22X3+2a23X2X3 +a3X3 ay a(XAX) 就 ay ax ax X2 ay X X= 2a11X1+2a12X2+2a413Xg 2a2X1+2a22X2+2a23X3 2a13X1+2a23X2+2a33X3 a a12 13 =2AX A= a21 a2 23 二次型的导数 a31 32 03
1 2 1 2 1 3 1 3 2 XAX = a1 1X1 + 2a X X + 2a X X 23 2 3 2 + a22X2 + 2a X X 2 33X3 + a AX a X a X a X a X a X a X a X a X a X X X AX X Y X Y X Y X Y 2 2 2 2 2 2 2 2 2 2 ( ) 1 3 1 2 3 2 3 3 3 1 2 1 2 2 2 2 3 3 1 1 1 1 2 2 1 3 3 3 2 1 = + + + + + + = = = = 3 2 1 X X X X = 31 32 33 21 22 23 11 12 13 a a a a a a a a a A 二次型的导数
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《计量经济学》课程教学资源(试卷习题)第十章 随机时间序列(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第八章 线性回归模型扩展(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第九章 滞后变量模型(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第六章 自相关(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第二章 简单线性回归模型(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第五章 异方差(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第七章 随机解释变量(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第四章 多重共线性(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第三章 K元线性回归模型(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)第一章 计量经济学的基本问题(含答案).doc
- 《计量经济学》课程教学资源(试卷习题)2007-2008年春A卷答案.doc
- 《计量经济学》课程教学资源(试卷习题)2007-2008年春A卷试题.doc
- 《计量经济学》课程教学资源(教案)11 联立方程模型识别和估计.doc
- 《计量经济学》课程教学资源(教案)10 滞后变量模型.doc
- 《计量经济学》课程教学资源(教案)09 K元线性回归模型扩展.doc
- 《计量经济学》课程教学资源(教案)06 广义最小二乘法(GLS)与异方差.doc
- 《计量经济学》课程教学资源(教案)08 随机解释变量.doc
- 《计量经济学》课程教学资源(教案)07 自相关.doc
- 《计量经济学》课程教学资源(教案)05 多重共线性.doc
- 《计量经济学》课程教学资源(教案)02 简单线性回归模型.doc
- 《计量经济学》课程教学课件(PPT讲稿)04 K元线性回归模型.ppt
- 《计量经济学》课程教学课件(PPT讲稿)01 计量经济学基本问题.ppt
- 《计量经济学》课程教学课件(PPT讲稿)05 多重共线性(Multicollinearity).ppt
- 《计量经济学》课程教学课件(PPT讲稿)02 简单线性回归模型.ppt
- 《计量经济学》课程教学课件(PPT讲稿)06 广义最小二乘法(GLS)与异方差(Heteroskedasticity).ppt
- 《计量经济学》课程教学课件(PPT讲稿)08 随机解释变量.ppt
- 《计量经济学》课程教学课件(PPT讲稿)09 K元线性回归模型的扩展.ppt
- 《计量经济学》课程教学课件(PPT讲稿)11 联立方程模型的识别和估计.ppt
- 《计量经济学》课程教学课件(PPT讲稿)10 滞后变量模型.ppt
- 《计量经济学》课程教学课件(PPT讲稿)07 自相关(Autocorrelation).ppt
- 《计量经济学》课程教学课件(PPT讲稿)12 时间序列计量经济模型.ppt
- 《国际期货市场运作》课程教学大纲 International Futures Market Operation.doc
- 《国际期货市场运作》课程授课教案(讲义,英文版).doc
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 1 The Journey Ahead.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 0 International Futures Markets Operation.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 2 Beginning with the Basics.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 3 The Modern Futures Exchange.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 7 Hedging with Spreads.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 6 Getting Started in Trading Futures.ppt
- 《国际期货市场运作》课程教学课件(PPT讲稿)Chapter 5 The Variety of Futures Markets.ppt
