《计量经济学》课程教学课件（PPT讲稿）09 K元线性回归模型的扩展

中国发者大学每奢管理学院 COLLEGE OF ECONOMICS MANASEMENT.CAL 第九章 K元线性回归模型的扩展

第九章 K元线性回归模型的扩展

中国農常大学每濟管猩学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 扩展（引申）的方面： 一、 模型估计方法由O儿S法向ML法的扩展； 二、线性向非线性数学形式的扩展； 三、单一方程模型向联立方程模型模型规模的扩展； 四、时间变量、虚拟变量也作为解释变量； 五、「检验应用于模型结构及稳定性检验； 六、模型检验方法的扩展

扩展（引申）的方面： 一、模型估计方法由OLS法向ML法的扩展； 二、线性向非线性数学形式的扩展； 三、单一方程模型向联立方程模型模型规模的扩展； 四、时间变量、虚拟变量也作为解释变量； 五、F检验应用于模型结构及稳定性检验； 六、模型检验方法的扩展

中固发者大学每奢管理学院 COLLEGE OF ECONOMICS MANASEMENT.CAL 一、 估计方法的扩展-极大似然估计(ML) 似然函数： f化，X,yp,o)=(2πa)2ewp(-Y-XpY-X 2a2 记为： LB./Y,X)-(2xo)expl-(Y-XB)(Y-XB) 201 hi=32)-h-心-0w-m 2o2 将上式对0、求偏导， b=(XXX'Y 令偏导为零，求得 ee MLE: n

一、估计方法的扩展-极大似然估计(ML) n e e S b X X X Y e  = =   − 2 1 ( ) ) 2 ( ) ( ) ( , , , , ) (2 ) exp( 2 2 2 2 1 2 u n n u u Y X Y X f Y Y Y X        −  − = − −  ] 2 ( ) ( ) ( , / , ) (2 ) exp[ 2 2 2 2 u n u u Y X Y X L Y X        −  − = − − 2 2 2 ( ) ( ) ln 2 (2 ) 2 ln u u n n Y X Y X L      −  − = − − − 似然函数: 记为: 将上式对 、求偏导， 令偏导为零，求得 MLE： 

中国農常大学每濟管猩学院 COLLEGE OF ECONOMICS MANAGEMENT.CAU 数学形式扩展非线性回归模型 1、可变换为线性的模型的估计 C-D函数 O=AKaIBe 两边同时取对数： InO=In 4+aIn K+BIn L+u 这里： a(nQ).△Q/Q a(nQ)△Q/Q a= anK)△K/K B、 anL)△L/L α、B为产出分别对资本、劳动的弹性系数。 在EViews中如何估计C-D函数？ 线性方式(OLS)、非线性方式(NLS)

二、数学形式扩展-非线性回归模型 u Q AK L e   = ln Q = ln A+ ln K +  ln L +u 1、可变换为线性的模型的估计 C-D函数 两边同时取对数: 这里: L L Q Q L Q K K Q Q K Q / / (ln ) (ln ) / / (ln ) (ln )      =       =  α、β为产出分别对资本、劳动的弹性系数。 在EViews中如何估计C-D函数？ ——线性方式（OLS）、非线性方式（NLS）

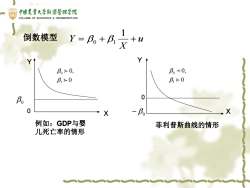
中國農背大学每奢管理学院 COLLEGE OF ECONOMICS MANASEMENT.CAU 倒数模型 1 Y=B。+B B>0, B。0 月>0 Bo 0 0 X -Bo 例如：GDP与婴 菲利普斯曲线的情形 儿死亡率的情形

倒数模型 u X Y = + + 1 0 1 X Y 0 0, 1 0     例如：GDP与婴 儿死亡率的情形 X Y 0  0 −  0 0 0, 1 0     0 菲利普斯曲线的情形

中国農常大学每濟管猩学院 COLLEGE OF ECONOMICS MANASEMENT.CAU 总成本函数C=B。+BX+B,X2+B,X3+u 1 S型曲线 Y= 熟练使用 Bo+Be-x Genr命令 双曲函数 =+是 X 双对数函数 hY=B。+B,hX 非线性模型线性 化后运用OLS法 可用于测度弹性 进行估计 半对数函数 hY=F。+Bt 可用于测度Y的平均增长速度

X e Y − + = 0 1 1   C = + X + X + X + u 3 3 2 0 1  2  Y X 1 0 1  =  + 总成本函数 熟练使用 Genr 命令 S型曲线 非线性模型线性 化后运用OLS法 进行估计 双曲函数 双对数函数 ln Y = 0 + 1 ln X Y t 0 1 半对数函数 ln =  +  可用于测度弹性 可用于测度Y的平均增长速度

中固发章大学每奢管理学院 COLLEGE OF ECONOMICS乡NT,CA 希克斯中性技术进步的C-D生产函数：技术进步前后，劳动的产出弹 性与资本的产出弹性同步增长，KL不随时间变化) Y=A(1)K(L (t) =(Ae")K(t)L(1) m表示技术进步率 取对数得： In Y=In 4+aIn K(t)+BIn L(t)+mt d(In Y)1 dy 1 dK 1 dl 微分得： X +B +m dt y dt K dt L dt a、B为资 产出增 资本增 劳动增 本弹性和劳 长率，记 长率，记 长率，记 动弹性 为y 为K 为L

希克斯中性技术进步的C-D生产函数：技术进步前后，劳动的产出弹 性与资本的产出弹性同步增长，K/L不随时间变化） ( ) ( ) ( ) ( ) ( ) ( ) 0 A e K t L t Y A t K t L t mt     = = m 表示技术进步率 取对数得： ln Y = ln A + ln K(t) + ln L(t) + mt 0   微分得: m dt dL dt L dK dt K dY dt Y d Y = =  +  + (ln ) 1 1 1   产出增 长率,记 为y 资本增 长率,记 为K 劳动增 长率,记 为L α、β为资 本弹性和劳 动弹性

中国農業大学每奢管理学院 COLLEGE OF ECONOMICS MANASEMENT.CAL 技术进步率为： 1Y-a: 1 dk-B. 1 dl m= y dt K dt I dt 即： m=y-C·k-B·1←一索洛增长速度方程 技术进步贡献率： E1="mx100% 资本贡献率： ·k B=a ×100% E4+E,+Ex=1 y 劳动贡献率： E,=B-1×100%

技术进步率为： dt dL dt L dK dt K dY Y m 1 1 1 = −  −   即： m = y −  k −  l 索洛增长速度方程 技术进步贡献率： = 100% y m EA 资本贡献率： 劳动贡献率： 100%  = y k Ek  100%  = y l El  + + =1 EA EL EK

中国爱青大学每奢管理学院 COLLEGE OF ECONOMICS MANASEMENT.CAL 2、不可变换为线性的模型的估计，例： CES (Constant Elasticity of Substitution) 生产函数 Q=A(61KP+6,LP)Pe“ A:为规模参数（效率参数），反映技术发达程度； :分布参数，反映劳动密集程度。6，+δ，=1 p:替代参数 m:规模报酬参数

2、不可变换为线性的模型的估计，例： ◆ CES（Constant Elasticity of Substitution） 生产函数 u m Q A K L e      − − − = ( + ) 1 2 A :为规模参数(效率参数), 反映技术发达程度; δ:分布参数, 反映劳动密集程度。δ1+δ2=1 ρ:替代参数. m: 规模报酬参数

中国農常大学每濟管猩学院 COLLEGE OF ECONOMICS MANASEMENT.CAL ◆泰勒级数展开法 (1) 非线性模型Y=f(X1,X2,XkB1,B2,Bp)+u (2)给定一组参数的初始值bo,b20,b0，将上式展开 r=x名.n+空器6-刻) 60b6,-bK6,-b+.+ i1 (3)取上式的前两项，得原函数近似线性表达式，用OLS 法进行估计，得出新的一组参数估计值b1,b21,b1,重复以上 过程，直到： (4) bt- b <6时，迭代结束

Y f X X X u = ( 1 , 2 ,., k; 1 ,  2 ,.,  p ) + ◆泰勒级数展开法 b b b b u b b f b b b f Y f X X X b b b b b i i j j i j p j p i i p i b i i k p i j i − − ++    + −   =  +    = = = ( ) ( )( ) 2 1 ( , , , ; , ,., ) ( ) ( ) 0 0 2 1 1 0 1 1 2 1 0 2 0 0 0 0 0 （3）取上式的前两项，得原函数近似线性表达式，用OLS 法进行估计，得出新的一组参数估计值 b11,b21,.,bp1 ，重复以上 过程，直到： （1）非线性模型 （2）给定一组参数的初始值 ，将上式展开 （4） ij ij ij b b +1 − b ＜δ 时，迭代结束。 10 20 0 , ,., b b bp