《计量经济学》课程教学资源（试卷习题）第九章 滞后变量模型（含答案）

第九章滞后变量模型 一单项选择题 1下列属于有限分布滞后模型的是(。 A.Y=a+box,+br+by2++u B.Y=a+bX,+bX,+.+w, C.Y.=a+box,+br+b2Y-2+.+by+u D.Y,=a+boX,+bx+b2X-2++b+u 2消费函数模型C,=400+0.5L,+0.31+0.1山-2，其中1为收入，则当期收入1。 对未来消费C2的影响是：I增加1单位，C2增加( A.0.5单位 B.0.3单位 C0.1单位 D.0.9单位 3在分布滞后模型y,=a+bX,+bX,+b2X,2+.+bX,-t+山，中，长期乘数 为 A.bo B.b(i=1,2,k) CXA D. 4.在分布滞后模型的估计中，使用时间序列资料可能存在的序列相关问题就表现为 ( A异方差问题 B.自相关问题 C.多重共线性问题 D.随机解释变量问题

第九章 滞后变量模型 一. 单项选择题 1.下列属于有限分布滞后模型的是( )。 A. Yt = +b0Xt +b1Yt−1 +b2Yt−2 ++ut B. Yt = + b0Xt + b1Xt−1 ++ ut C. Yt = + b0Xt + b1Yt−1 + b2Yt−2 ++ bkYt−k + ut D. Yt = + b0Xt + b1Xt−1 + b2Xt−2 ++ bk Xt−k + ut 2.消费函数模型 1 1 2 400 0.5 0.3 0. ˆ t = + t + t− + t− C I I I ，其中 I 为收入，则当期收入 It 对未来消费 Ct+2 的影响是：I 增加 1 单位，Ct+2 增加( )。 A. 0.5 单位; B. 0.3 单位 C. 0.1 单位; D. 0.9 单位 3.在分布滞后模型 Yt = + b0 Xt + b1Xt−1 + b2 Xt−2 ++ bk Xt−k + ut 中，长期乘数 为( )。 A. 0 b B. i b (i=1,2,.,k) C. = k i i b 1 D. = k i i b 0 4.在分布滞后模型的估计中，使用时间序列资料可能存在的序列相关问题就表现为 ( )。 A.异方差问题 B.自相关问题 C.多重共线性问题 D.随机解释变量问题

5对于有限分布滞后模型y,=a+bX,+X+b,X2++b,X,4+4,中，如果其 参数b,(1,2,k)可以近似地用一个关于滞后长度i(=1,2.k)的多项式表示，则称 此模型为()。 A有限多项式滞后模型 B无限多项式滞后模型 C考伊克变换模型 D.自适应预期模型 6.自适应预期模型基于如下的理论假设：影响被解释变量Y,的因素不是X而是关于 X的预期X,且预期X形成的过程是X-X,=y(X,-X),其中0<Y<1,Y被 称为()。 A衰减率 B预期系数 C.调整因子 D.预期误差 7.当分布滞后模型的随机误差项满足线性模型假定时，下列哪一个模型可以用最小 二乘法来估计( A.Y=a+box,+bX+bx-2++bx+u B.y,=al-)+bX,+2Y-+4-u C.y,=b+bX,+(1-y)Y+4,-1-y)u D.Y,=b。+b1X,+(1-8)Y,-1+4, 8.下列哪个模型的一阶自相关问题可用DW检验( A有限多项式分布滞后模型 B.自适应预期模型 C.库伊克变换模型 D.局部调整模型 9.有限多项式分布滞后模型中，通过将原分布滞后模型中的参数表示为滞后期的有 限多项式，从而克服了原分布滞后模型估计中的()。 A异方差问题 B.序列相关问题：

5.对于有限分布滞后模型 t t t t k t k t Y = + b X + b X + b X + + b X + u  0 1 −1 2 −2  − 中，如果其 参数 i b (i=1,2,., k) 可以近似地用一个关于滞后长度 i (i=1,2,.,k) 的多项式表示，则称 此模型为（ ）。 A.有限多项式滞后模型 B.无限多项式滞后模型 C.考伊克变换模型 D.自适应预期模型 6.自适应预期模型基于如下的理论假设：影响被解释变量 Yt 的因素不是 Xt ,而是关于 X 的预期 * Xt+1 ，且预期 * Xt+1 形成的过程是 * Xt+1 - * Xt = ( ) * Xt − Xt+1  ，其中 0＜γ＜1，γ 被 称为（ ）。 A.衰减率 B.预期系数 C.调整因子 D.预期误差 7.当分布滞后模型的随机误差项满足线性模型假定时，下列哪一个模型可以用最小 二乘法来估计（ ）。 A. t t t t k t k t Y = +b X +b X +b X + +b X +u  0 1 −1 2 −2  − B. 0 1 1 (1 ) t = − + t + t− + t − t− Y   b X Y u u C. 0 1 1 1 (1 ) (1 ) Yt = b + b Xt + − Yt− + ut − − ut−     D. Yt =b0 + b1Xt + − Yt−1 + ut (1 ) 8.下列哪个模型的一阶自相关问题可用 DW 检验（ ）。 A.有限多项式分布滞后模型 B.自适应预期模型 C.库伊克变换模型 D.局部调整模型 9.有限多项式分布滞后模型中，通过将原分布滞后模型中的参数表示为滞后期 i 的有 限多项式，从而克服了原分布滞后模型估计中的（ ）。 A. 异方差问题; B. 序列相关问题；

C,多重共线性问题：D.因包含无穷多个参数从而不可能被估计的问题 10.分布滞后模型y,=a+b,X,+b,X,-+b,X,-2+bX,-+u,中，为了使模型的自 由度达到30，必须拥有多少年的观测资料（)， A32B.33 C.34 D.35 二、名词解释 1.滞后变量： 2.滞后效应 3.多项式分布滞后模型 4短期乘数和长期乘数： 5.自回归分布滞后模型； 6.自回归模型 三、问答题 1滞后外生变量模型和滞后内生变量模型的概念是什么？ 2滞后变量横型有哪几种类型？外生变量分布滞后模型使用0LS方法存在哪些问 题？ 3被解释变量对于一个或者多个解释变量反应滞后的原因是什么？给出一些分布滞 后模型的例子， 4.叙述用阿尔蒙多项式法估计外生变量有限分布滞后模型的方法步骤，对多项式的 次数r有哪些限制，为什么？4.滞后变量模型的作用是什么？ 5,有限分布滞后模型估计的困难是什么？ 6.什么是经验加权估计法？常见的滞后结构类型有那几种？ 7.经验加权估计法的优缺点、通常做法是什么？

C. 多重共线性问题; D. 因包含无穷多个参数从而不可能被估计的问题 10.分布滞后模型 Yt = + b0 Xt + b1Xt−1 + b2 Xt−2 + b3Xt−3 + ut 中，为了使模型的自 由度达到 30，必须拥有多少年的观测资料（ ）。 A.32 B.33 C.34 D.35 二、名词解释 1.滞后变量； 2.滞后效应； 3.多项式分布滞后模型 4.短期乘数和长期乘数； 5.自回归分布滞后模型； 6.自回归模型 三、问答题 1.滞后外生变量模型和滞后内生变量模型的概念是什么？ 2.滞后变量模型有哪几种类型？外生变量分布滞后模型使用 OLS 方法存在哪些问 题？ 3.被解释变量对于一个或者多个解释变量反应滞后的原因是什么？给出一些分布滞 后模型的例子。 4. 叙述用阿尔蒙多项式法估计外生变量有限分布滞后模型的方法步骤，对多项式的 次数 r 有哪些限制，为什么？4．滞后变量模型的作用是什么？ 5．有限分布滞后模型估计的困难是什么？ 6. 什么是经验加权估计法？常见的滞后结构类型有那几种？ 7．经验加权估计法的优缺点、通常做法是什么？

8.什么是阿尔蒙估计法？其基本原理是什么？ 9.阿尔蒙估计法多项式的次数如何确定？滞后期长度如何确定？ 10.什么是考伊克变换？意义何在？ 11.考伊克模型的特点是什么？缺陷是什么？ 12.什么是预期模型？难点是什么？如何解决？ 13,什么是自适应预期模型？它是如何解决预期模型难点的？ 14.考伊克模型、自适应预期模型和局部调整模型有何异同？模型估计会存在哪些 困难？如何解决？ 15.检验一阶自回归模型随机误差项是否存在自相关，为什么用德宾h检验而不用 DW检验？ 16.什么是局部调整模型？什么是局部调整假设？ 四、实验题 1.考察以下分布滞后横型 Y.=a+box,+bx+b2X-2+bX-3+bX+bsX-s+u 假如用2阶有限多项式变换估计这个模型后得 y,=0.85+0.50Zom+0.45Z.-0.10Z,+4, 式中： -2.Z-2石-2x (1)求原模型中各参数的估计值； (2)试估计X对Y的短期乘数、中期乘数和长期乘数。 2.对于下列估计模型

8．什么是阿尔蒙估计法？其基本原理是什么？ 9．阿尔蒙估计法多项式的次数如何确定？滞后期长度如何确定？ 10．什么是考伊克变换？意义何在？ 11．考伊克模型的特点是什么？缺陷是什么？ 12．什么是预期模型？难点是什么？如何解决？ 13．什么是自适应预期模型？它是如何解决预期模型难点的？ 14．考伊克模型、自适应预期模型和局部调整模型有何异同？模型估计会存在哪些 困难？如何解决？ 15．检验一阶自回归模型随机误差项是否存在自相关，为什么用德宾 h 检验而不用 DW 检验？ 16．什么是局部调整模型？什么是局部调整假设？ 四、实验题 1.考察以下分布滞后模型： Yt = + b0Xt + b1Xt−1 + b2Xt−2 + b3Xt−3 + b4Xt−4 + b5Xt−5 + ut 假如用 2 阶有限多项式变换估计这个模型后得 t t t t t Y = + Z + Z − Z + u 0 1 2 0.85 0.50 0.45 0.10 式中： ; 3 0 0 = = − i Z t Xt i ; 3 0 1 = = − i t t i Z iX ; 3 0 2 2 = = − i t Xt i Z i （1）求原模型中各参数的估计值； （2）试估计 X 对 Y 的短期乘数、中期乘数和长期乘数。 2.对于下列估计模型：

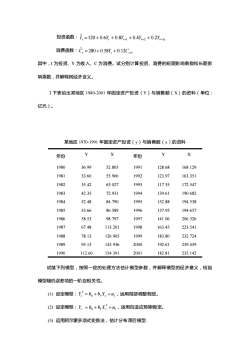
投资函数：1，=120+0.6Y,+0.8Y,1+0.4Y-2+02Y- 消费函数：C,=280+0.58Y+0.12C 其中，I为投资、Y为收入、C为消费。试分别计算投资、消费的短期影响乘数和长期影 响乘数，并解释其经济含义 3.下表给出某地区1980-2001年固定资产投资(Y)与销售额(X)的资料（单位： 亿元). 某地区1970-1991年固定资产投资(y）与销售额(x)的资料 年份 Y 年份 Y 1980 36.99 52.805 1991 128.68 168.129 1981 33.60 55.906 1992 123.97 163.351 1982 35.42 63.027 1993 117.35 172.547 1983 42.35 72.931 1994 139.61 190.682 1984 52.48 84.790 1995 152.88 194.538 1985 53.66 86.589 1996 137.95 194.657 1986 58.53 98.797 1997 141.06 206.326 1987 67.48 113.201 1998 163.45 223.541 1988 78.13 126.905 1999 183.80 232.724 1989 95.13 143.936 2000 192.61 239.459 1990 112.60154.391 2001 182.81 235.142 试就下列模型，按照一定的处理方法估计模型参数，并解释模型的经济意义，检验 模型随机误差项的一阶自相关性。 ()设定模型：y=b。+bX,+4,运用局部调整假定。 (2)设定模型：y,=b,+bX,+4,运用自适应预期假定。 ()运用阿尔蒙多项式变换法，估计分布滞后模型

投资函数： t t t t t t I Y Y 1 Y 2 2Y 3 120 0.6 0.8 0.4 0. ˆ = + + − + − + − 消费函数： 12 1 280 0.58 0. ˆ Ct = + Yt + Ct− 其中，I 为投资、Y 为收入、C 为消费。试分别计算投资、消费的短期影响乘数和长期影 响乘数，并解释其经济含义。 3.下表给出某地区 1980-2001 年固定资产投资（Y）与销售额（X）的资料（单位： 亿元）。 某地区 1970-1991 年固定资产投资（y）与销售额（x）的资料 年份 Y X 年份 Y X 1980 36.99 52.805 1991 128.68 168.129 1981 33.60 55.906 1992 123.97 163.351 1982 35.42 63.027 1993 117.35 172.547 1983 42.35 72.931 1994 139.61 190.682 1984 52.48 84.790 1995 152.88 194.538 1985 53.66 86.589 1996 137.95 194.657 1986 58.53 98.797 1997 141.06 206.326 1987 67.48 113.201 1998 163.45 223.541 1988 78.13 126.905 1999 183.80 232.724 1989 95.13 143.936 2000 192.61 239.459 1990 112.60 154.391 2001 182.81 235.142 试就下列模型，按照一定的处理方法估计模型参数，并解释模型的经济意义，检验 模型随机误差项的一阶自相关性。 (1) 设定模型： Yt = b0 + b1Xt + ut * ，运用局部调整假定。 (2) 设定模型： Yt = b + b Xt + ut * 0 1 ，运用自适应预期假定。 (3) 运用阿尔蒙多项式变换法，估计分布滞后模型:

Y.=a+box,+bx+bx2+bx3+bX+u 4.对线性回归模型： y=XB+4,（1=1,2,.,n) 满足E(X,4,)≠0。假定Z,可以作为X,合适的工具变量，且Va(d2)=o2I,请导 出工具变量估计量，并给出它的极限分布。 5.一般的几何滞后分布模型具有形式： y,=a+B∑0-yx-+8,，Ee,)=0,Cos,e)=o6,0<<1。 如何对这类模型进行估计，才能获得具有较好性质的参数估计量？ 参考答案： 一、单项选择题 1D,2.C3.D4.C,5.A;6.B7.D8.A;9.C10.D 二、名词解释 1滞后变量(Lag Variable):在现实经济运行中，某些经济变量不仅受同期各种因素的 影响，而且也受到过去某些时期的各种因素的影响，甚至受到自身的过去值的影响，如 居民的消费需求不仅受本期收入的影响还受到上期收入的影响，通常把这种过去时期的、 具有滞后作用的变量称为“滞后变量”， 2.滞后效应(Lag Effect):对于解释变量的任何变化，被解释变量必然会做出反映 而这些反映往往是要经过一段时间之后才会表现出来，称这种现象为滞后效应， 3.多项式分布滞后模型(Poly nomial Auto-regressive Distributed Lag,PDL):模型中没 有滞后被解释变量，本期被解释变量,仅与解释变量的当期值X,及其若干期的滞后值

Yt = + b0 Xt + b1Xt−1 + b2 Xt−2 + b3Xt−3 + b4Xt−4 + ut 4. 对线性回归模型： Yi = Xi + ui ， （ i = 1,2,  ,n ） 满足 E(Xiui )  0 。假定 Zi 可以作为 Xi 合适的工具变量，且 Var u Z I 2 ( ) =  ，请导 出工具变量估计量，并给出它的极限分布。 5．一般的几何滞后分布模型具有形式： ( )  = = + − − + 0 1 i t i t i t y     x  ， E( t ) = 0， ( ) Cov t s t,s 2  , =  ，0   1 。 如何对这类模型进行估计，才能获得具有较好性质的参数估计量？ 参考答案： 一、单项选择题 1.D; 2.C; 3.D; 4.C; 5.A; 6.B; 7.D; 8.A; 9.C; 10.D 二、名词解释 1.滞后变量(Lag Variable)：在现实经济运行中，某些经济变量不仅受同期各种因素的 影响，而且也受到过去某些时期的各种因素的影响，甚至受到自身的过去值的影响，如： 居民的消费需求不仅受本期收入的影响还受到上期收入的影响，通常把这种过去时期的、 具有滞后作用的变量称为“滞后变量”。 2.滞后效应（Lag Effect）：对于解释变量的任何变化，被解释变量必然会做出反映， 而这些反映往往是要经过一段时间之后才会表现出来，称这种现象为滞后效应。 3.多项式分布滞后模型（Polynomial Auto-regressive Distributed Lag, PDL）：模型中没 有滞后被解释变量，本期被解释变量 Yt 仅与解释变量的当期值 Xt 及其若干期的滞后值

X,1,X,2,.等有关，这样的模型就是多项式分布滞后模型。由两种形式：有限多项式 分布滞后模型： y,=a+BX,+BX-1+.+BX,-k+4, 和无限多项式分布滞后模型 y,=a+B。X,+BX,+B2X-2+.+4, 4短期乘数和长期乘数：多项式分布滞后模型中，系数B表示随着X的单位变化，Y 值的同期变化，称之为短期乘数，（0+B1++B)(i≥3)反映了近几期X的单位变化对Y 的影响，称之为中期乘数：反映所有期X的单位变化对Y的影响可以通过如下表达式给出 空A=风+风+民++风=B 称之为长期乘数（假定该表达式B存在） 为了更便于描述各分布滞后项对于被解释变量的作用大小，对各项系数进行“标准 化，即： 、BB P:-B.B 其中，阝：表示X在某一时期的变化对Y的影响占长期影响（长期乘数）的比例，以便 于对各滞后项对Y影响作用大小进行比较 5.自回归分布滞后模型(Auto-regressive Distributed Lag,ADL) Y,=a+aY+B。X,+4, 6.自回归模型(Auto Regressive Model) 自回归模型指被解释变量Y的滞后变量Y作为解释变量的模型，由于是被解释变 量的滞后期变量对被解释变量现期的回归，即自己回归自己而得名

Xt−1 , Xt−2 ,  等有关，这样的模型就是多项式分布滞后模型。由两种形式：有限多项式 分布滞后模型： Yt =  + 0Xt + 1Xt−1 ++ k Xt−k + ut 和无限多项式分布滞后模型： Yt = +  0Xt + 1Xt−1 +  2Xt−2 ++ ut 4.短期乘数和长期乘数：多项式分布滞后模型中，系数β0表示随着X的单位变化，Y 值的同期变化，称之为短期乘数，（β0+β1+.+βi）（i ≥3）反映了近几期X的单位变化对Y 的影响，称之为中期乘数；反映所有期X的单位变化对Y的影响可以通过如下表达式给出， 即  =  +  +  + +  =  = k k i i . 0 1 2 0 称之为长期乘数（假定该表达式 β 存在）。 为了更便于描述各分布滞后项对于被解释变量的作用大小，对各项系数进行“标准 化”，即：      i i i i = =   其中，β * i 表示 X 在某一时期的变化对 Y 的影响占长期影响（长期乘数）的比例，以便 于对各滞后项对 Y 影响作用大小进行比较。 5.自回归分布滞后模型（Auto-regressive Distributed Lag, ADL） Yt = 0 +1Yt−1 +  0 Xt + ut 6.自回归模型(Auto Regressive Model) 自回归模型指被解释变量 Y 的滞后变量 Yt−1 作为解释变量的模型，由于是被解释变 量的滞后期变量对被解释变量现期的回归，即自己回归自己而得名

三、问答题 1.答：如果滞后变量模型中只包括了解释变量的若干滞后变量，形如下式： Y=a+Box,+BX++Bx+u 这种模型称为分布滞后模型或外生滞后变量模型：如果滞后变量模型中不仅包括解释变 量，还包括了被解释变量的若干滞后变量的模型，形如下式： y,=a+R,+BY+B,Y2+.+4 这种模型称为自回归模型或内生滞后变量模型。 2.答：滞后变量模型有分布滞后模型和自回归模型两大类，其中：分布滞后模型有 无限分布滞后模型和有限分布滞后模型；自回归模型又有柯克模型、自适应预期模型和 部分调整模型。外生变量分布滞后模型使用OLS法存在以下问题：1对于无限期的分布 滞后模型，由于样本观测值的有限性，使得无法直接对其进行估计；(2对于有限期的分 布滞后模型，使用0L$方法会遇到：没有先验准则确定滞后期长度，对最大滞后期的确 定往往带有主观随意性；如果滞后期较长，由于样本容量有限，当滞后变量数目增加时 必然使得自由度减少，将缺乏足够的自由度进行估计和检验；同名变量滞后值之间可能 存在高度线性相关，即模型存在高度的多重共线性。 3.答：被解释变量对于一个或者多个解释变量反应滞后的原因是：心理因素使得其 行为方式滞后于经济形势的变化；技术性原因使得当年的产出在某种程度上依赖于过去 若干期内投资形成的固定资产制度性原因使得人们对某些外部变化不能立即做出反应。 下面是分布滞后模型的例子 (1)消费支出Y,为先期个人可支配收入PDI的函数： Y,=Bo+B.PDI,+B.PDI+B.PDI+u (2)耐用品存量调整模型：

三、问答题 1. 答：如果滞后变量模型中只包括了解释变量的若干滞后变量，形如下式： Yt =  + 0Xt + 1Xt−1 ++ k Xt−k + ut 这种模型称为分布滞后模型或外生滞后变量模型；如果滞后变量模型中不仅包括解释变 量，还包括了被解释变量的若干滞后变量的模型，形如下式： Yt =  + 0Yt + 1Yt−1 + 2Yt−2 ++ ut 这种模型称为自回归模型或内生滞后变量模型。 2．答：滞后变量模型有分布滞后模型和自回归模型两大类，其中：分布滞后模型有 无限分布滞后模型和有限分布滞后模型；自回归模型又有柯克模型、自适应预期模型和 部分调整模型。外生变量分布滞后模型使用 OLS 法存在以下问题：⑴对于无限期的分布 滞后模型，由于样本观测值的有限性，使得无法直接对其进行估计；⑵对于有限期的分 布滞后模型，使用 OLS 方法会遇到：没有先验准则确定滞后期长度，对最大滞后期的确 定往往带有主观随意性；如果滞后期较长，由于样本容量有限，当滞后变量数目增加时， 必然使得自由度减少，将缺乏足够的自由度进行估计和检验；同名变量滞后值之间可能 存在高度线性相关，即模型存在高度的多重共线性。 3. 答：被解释变量对于一个或者多个解释变量反应滞后的原因是：心理因素使得其 行为方式滞后于经济形势的变化；技术性原因使得当年的产出在某种程度上依赖于过去 若干期内投资形成的固定资产；制度性原因使得人们对某些外部变化不能立即做出反应。 下面是分布滞后模型的例子： （1）消费支出 Yt 为先期个人可支配收入 PDI 的函数： Yt = 0 + 1PDIt + 2PDIt−1 + 3PDIt−2 + ut （2）耐用品存量调整模型：

2,=R。+Bl,+B,2+u, 4.答：(1)由于社会经济的发展、经济行为的形城与演变在很大程度上都与前期 的经济活动密切相关，滞后变量模型可以更全面、客观地描述经济现象，提高模型的拟 合程度。 (2)滞后变量模型可以反映过去的经济活动对现期经济行为的影响，从而描述了经 济活动的运动过程，使模型成为动态模型。 (3)滞后变量模型可以模拟分析经济系统的变化和调整过程。 5.答：(1)损失自由度。(2)产生多重共线性。（3)滞后长度难以确定。 6.答：根据实际经济问题的特点及经验判断，对滞后变量赋予一定的权数，构成各 滞后变量的线性组合，形成新的变量，再用最小二乘法进行估计。其基本思路是减少模 型中被估计的参数个数。 常见的滞后结构类型有：递减滞后结构、不变滞后结构和A型滞后结构。 7.答：优点是简单易行、不损失自有度、避免多重共线性和参数估计具有一致性等。 缺点是设置权数的主观随意性较大，要求对实际问题的特征具有比校透彻的了解。通常 的做法是多选几组权数分别进行估计，根据检验统计量选取最佳方程。 8.答：利用有限多项式来减少待估参数的数量，以减少多重共线性和参数估计中的 自由度损失。其基本原理是，如果有限分布滞后模型 Y=a+box,+bX+bX-2+.+bX+u 的参数(i=1,2,.,k)的分布可以近似地用一个关于i的低阶多项式表示，就可以 利用多项式减少模型中的参数

t t Qt ut Q = 0 + 1 I + 2 −1 + 4．答：（1）由于社会经济的发展、经济行为的形成与演变在很大程度上都与前期 的经济活动密切相关，滞后变量模型可以更全面、客观地描述经济现象，提高模型的拟 合程度。 （2）滞后变量模型可以反映过去的经济活动对现期经济行为的影响，从而描述了经 济活动的运动过程，使模型成为动态模型。 （3）滞后变量模型可以模拟分析经济系统的变化和调整过程。 5．答：（1）损失自由度。（2）产生多重共线性。（3）滞后长度难以确定。 6. 答：根据实际经济问题的特点及经验判断，对滞后变量赋予一定的权数，构成各 滞后变量的线性组合，形成新的变量，再用最小二乘法进行估计。其基本思路是减少模 型中被估计的参数个数。 常见的滞后结构类型有：递减滞后结构、不变滞后结构和 A 型滞后结构。 7．答：优点是简单易行、不损失自有度、避免多重共线性和参数估计具有一致性等。 缺点是设置权数的主观随意性较大，要求对实际问题的特征具有比较透彻的了解。通常 的做法是多选几组权数分别进行估计，根据检验统计量选取最佳方程。 8．答：利用有限多项式来减少待估参数的数量，以减少多重共线性和参数估计中的 自由度损失。其基本原理是，如果有限分布滞后模型 Yt = + b0Xt + b1Xt−1 + b2Xt−2 ++ bk Xt−k + ut 的参数 bi ( i = 1，2，.，k) 的分布可以近似地用一个关于 i 的低阶多项式表示，就可以 利用多项式减少模型中的参数

9.答：依据经济理论和实际经验加以确定。之后结构为递减型和常数型时选择一次 多项式，倒V型选择二次多项式，有两个转向点时选择三次多项式。在实际应用中，一 般取2或3，很少超过4. 可以依据经济理论和实际经验加以确定，也可通过一些统计检验辅助确定滞后期长 度。常用的统计检验有：相关系数、调整可决系数和施瓦茨准则。 10,答：特点是原理巧妙、简单、实用，具有充分柔性，有效消除了自由度损失问 题。缺点是需要事先确定之后期长度和多项式次数，如何确定比较困难，实际确定往往 带有主观性。 11.答：如果无限分布滞后模型 y,=a+bX,+bX,4+b2X,-2+.+4, 中的参数b,是按几何级数列衰减的，即 bi=bo (0<元<1,1=1,2，) 其中，b为常数，公比入为待估参数，则称为几何分布滞后模型，（也称Koyck模型）。 几何分布滞后模型的基本假设是：随着滞后期的增加，滞后变量对被解释变量的影 响越来越小。这一假定在很多情况下是合理的。 12,答：将几何分布滞后模型 y,=a+bX,+b2X4+b2X-2++4, 变形为 y=a1-2)+bX,+1+叫 其中，山=山，-山1，称为考伊克变换

9．答：依据经济理论和实际经验加以确定。之后结构为递减型和常数型时选择一次 多项式，倒 V 型选择二次多项式，有两个转向点时选择三次多项式。在实际应用中，一 般取 2 或 3，很少超过 4。 可以依据经济理论和实际经验加以确定，也可通过一些统计检验辅助确定滞后期长 度。常用的统计检验有：相关系数、调整可决系数和施瓦茨准则。 10．答：特点是原理巧妙、简单、实用，具有充分柔性，有效消除了自由度损失问 题。缺点是需要事先确定之后期长度和多项式次数，如何确定比较困难，实际确定往往 带有主观性。 11．答：如果无限分布滞后模型： Yt = + b0Xt + b1Xt−1 + b2Xt−2 ++ ut 中的参数 bi 是按几何级数列衰减的，即 bi = b0 λ i (0 < λ < 1，I = 1，2，.) 其中，b0 为常数，公比 λ 为待估参数，则称为几何分布滞后模型，（也称 Koyck 模型）。 几何分布滞后模型的基本假设是：随着滞后期的增加，滞后变量对被解释变量的影 响越来越小。这一假定在很多情况下是合理的。 12．答：将几何分布滞后模型 Yt = + b Xt + b Xt− + b Xt−2 ++ ut 2  0 0 1 0 变形为  Yt = − + b0 Xt + Yt−1 + ut (1 )  其中， −1  ut = ut − ut ，称为考伊克变换