《计量经济学》课程教学资源（试卷习题）第二章 简单线性回归模型（含答案）

第二章简单线性回归分析 一、填空题 1计量经济模型增通最小二乘法的基本假定有 。 2被解释变量的观测值y与其回归理论值E(Y)之间的偏差，称为：被解释 变量的观值Y与其回归估计值，之间的偏差，称为 3.对线性回归模型Y-B。+BX+u进行最小二乘估计，最小二乘法的原理是 4高斯一马尔可夫定理证明在总体参数的各种线性无偏估计中，普通最小二乘估计量具 有 的特性并由此才使最小二乘法在数理统计学和计量经济学中获得了最广泛的 应用。 5.普通最小二乘法得到的参数估计量具有 、 统计性 金 6对于Y=b。+b,X,+b2X2+山，在给定置信水平下，减小b的置信区间的途径主要 7总平方和TSS反映 之离差的平方和；回归平方和ESS反映了 之离差的平方和；残差平方和RSS反映了 之差 的平方和。 8方程F显著性检验的含义是 9.解释变量t显著性检验的含义是 二、单选题

第二章 简单线性回归分析 一、填空题 1.计量经济模型普通最小二乘法的基本假定有_、_、_、 _。 2.被解释变量的观测值 Yi 与其回归理论值 E(Y) 之间的偏差，称为_；被解释 变量的观测值 Yi 与其回归估计值 Yi ˆ 之间的偏差，称为_。 3. 对线性回归模型 Y =  0 + 1X + u 进行最小二乘估计，最小二乘法的原理是 _。 4.高斯—马尔可夫定理证明在总体参数的各种线性无偏估计中，普通最小二乘估计量具 有_的特性，并由此才使最小二乘法在数理统计学和计量经济学中获得了最广泛的 应用。 5.普通最小二乘法得到的参数估计量具有_、_、_统计性 质。 6.对于 Y = b0 + b1X1 + b2X2 + u ，在给定置信水平下，减小 b 的置信区间的途径主要 有_、_、_。 7.总平方和 TSS 反映_之离差的平方和；回归平方和 ESS 反映了 _之离差的平方和；残差平方和 RSS 反映了_之差 的平方和。 8.方程 F 显著性检验的含义是_。 9.解释变量 t 显著性检验的含义是 。 二、单选题

1.回归分析中定义() A.解释变量和被解释变量都是随机变量 B.解释变量为非随机变量，被解释变量为随机变量 C.解释变量和被解释变量都为非随机变量 D.解释变量为随机变量，被解释变量为非随机变量 2.最小二乘原理是指使( )达到最小值的原则确定样本回归方程。 A2出-：B2郭-：cMg-》:D2出- 3.下图中“(”所指的距离是(） -X Y) i=b。+hX X A随机误差；B残差：C离差Y-了D.离差了-了 4.极大似然准则是从模型总体抽鲰n组样本观测值的( )最大的准则确定样 本回归方程。 A离差平方和；B,均值C概率；D方差 5.参数郊的统计量b是Y的线性函数称为参数估计量具有( )的性质。 A线性；B无偏性；C.有效性；D.一致性 6.参数的统计量b具备有效性是指( A.Var(b)=0 B.Var(b)为最小 C.b-B=0 D.(b-B)为最小

1. 回归分析中定义（ ） A. 解释变量和被解释变量都是随机变量 B. 解释变量为非随机变量，被解释变量为随机变量 C. 解释变量和被解释变量都为非随机变量 D. 解释变量为随机变量，被解释变量为非随机变量 2. 最小二乘原理是指使（ ）达到最小值的原则确定样本回归方程。 A. = − n i Yi Yi 1 ) ˆ ( ； B. = − n i Yi Yi 1 ˆ ； C. ) Max( ˆ Yi −Yi ； D. = − n i Yi Yi 1 2 ) ˆ ( 3. 下图中“｛”所指的距离是（ ） A. 随机误差； B. 残差； C. 离差 Y −Y ； D.离差 Y ˆ −Y 4. 极大似然准则是从模型总体抽取 n 组样本观测值的（ ）最大的准则确定样 本回归方程。 A.离差平方和； B.均值； C.概率； D.方差 5. 参数的统计量 b 是 Y 的线性函数称为参数估计量具有( )的性质。 A.线性； B.无偏性； C.有效性； D.一致性 6. 参数的统计量 b 具备有效性是指（ ） A. Var(b) = 0 B. Var(b) 为最小 C. b-=0 D. (b-)为最小 (X, Y ) Y ˆ = b0 + b1X Y Y X

7.已知含有截距项的三元线性回归模型估计的残差平方和为∑2=300，用于模型估 计的样本容量为n=24,则随机误差项u的方差估计量为( )。 A33.33;B.15;C.38.09;D.36.36 8.最常用的统计检验包括拟合优度检验、变量的1显著性检验和( ). A.方程的F显著性检验 B.多重共线性检验 C.异方差性检验 D.预则检验 9.反映由模型中解释变量所解释的那部分离差大小的是 A总体平方和 B回归平方和 C残差平方和 10.总体平方和TSS、残差平方和RSS与回归平方和ESS三者的关系是(). A RSs=TSS+ESS B.TSS=RSS+ESS C.ESS=RSS-TSS D.ESS-TSS+RSS 11.下面哪一个必定是错误的( )。 AY=20+0.3X,r=0.91B.=-35+0.2X,r=0.85 C.=15-2.3X,r=-0.78 D.=-67+0.76X,r=-0.89 12.产量(X,台)与单位产品成本(Y,元/台)之间的回归方程为Y=400-0.6X 这说明(）。 A.产量每增加一件，单位产品成本增加400元 B.产量每增加一件，单位产品成本减少0.6元 C.产量每增加一件，单位产品成本平均增加400元 D.产量每增加-件，单位产品成本平均减少0.6元 13.回归模型Y,=B。+BX,+4,i=1,.,25中，总体方差未知，检验H。:B=0 时，所省#乌号纵(

7. 已知含有截距项的三元线性回归模型估计的残差平方和为 300 2 e = ，用于模型估 计的样本容量为 n = 24 ，则随机误差项 u 的方差估计量为( )。 A. 33.33； B. 15； C. 38.09； D. 36.36 8. 最常用的统计检验包括拟合优度检验、变量的 t 显著性检验和（ ）。 A. 方程的 F 显著性检验 B. 多重共线性检验 C. 异方差性检验 D. 预测检验 9. 反映由模型中解释变量所解释的那部分离差大小的是( )。 A.总体平方和 B.回归平方和 C.残差平方和 10. 总体平方和 TSS、残差平方和 RSS 与回归平方和 ESS 三者的关系是（ ）。 A. RSS=TSS+ESS B. TSS=RSS+ESS C. ESS=RSS-TSS D. ESS=TSS+RSS 11. 下面哪一个必定是错误的（ ）。 A. 20 0.3 , 0.91 Y ˆ = + X r = B. 35 0.2 , 0.85 Y ˆ = − + X r = C. 15 2.3 , r 0.78 Y ˆ = − X = − D. 67 0.76 , r 0.89 Y ˆ = − + X = − 12. 产量（X，台）与单位产品成本（Y，元/台）之间的回归方程为 Y ˆ = 400 −0.6X ， 这说明（ ）。 A. 产量每增加一件，单位产品成本增加 400 元 B. 产量每增加一件，单位产品成本减少 0.6 元 C. 产量每增加一件，单位产品成本平均增加 400 元 D. 产量每增加一件，单位产品成本平均减少 0.6 元 13. 回归模型 Yi =  0 + 1Xi + ui ，i = 1，.，25 中，总体方差未知，检验 H0 : 1 = 0 时，所用的检验统计量 ( )1 1 1 S b b −  服从（ ）

Ax2(n-2):B.(n-1);C.x2(n-1);D.(n-2) 14.设k为回归模型中的参数个数（包括截距项），n为样本容量，RSS为残差平方和， ESS为回归平方和。则对总体回归模型进行显著性检验时构造的F统计量为(). A.F=ESS/(k-1) B.F=1-ESS/(-1) RSS /(n-k) RSS /(n-k) CF F-答 15.根据可决系数R?与F统计量的关系可知，当R?=1时有( A.F=l;B.F=-1;C.F+0;D.F0 16.线性回归模型的参数估计量b是随机变量Y的函数，即b=(XX)XY。所以b 是()。 A.随机变量；B.非随机变量；C.确定性变量；D.常量 17.由立，=X,b可以得到被解释变量的估计值，由于模型中参数估计量的不确定性 及随机误差项的影响，可知Y,是( ). A确定性变量；B.非随机变量；C.随机变量；D.常量 18.下面哪一表述是正确的( A线性国日楼型？=风+AX+W的零期望股是指之4=0 B.对模型Y=B。+B,X1+BX2+u进行方程显著性检验（即F检验），检验的零 假设是H。B。=B=B, C.相关系数较大意味着两个变量存在较强的因果关系 D.当随机误差项的方差估计量等于香时，说明被解释变量与解释变量之间为函数关系

A. ( 2) 2  n − ； B. t(n −1) ； C. ( 1) 2  n − ； D. t(n − 2) 14. 设 k 为回归模型中的参数个数（包括截距项），n 为样本容量，RSS 为残差平方和， ESS 为回归平方和。则对总体回归模型进行显著性检验时构造的 F 统计量为（ ）。 A. /( ) /( 1) RSS n k ESS k F − − = ; B. /( ) /( 1) 1 RSS n k ESS k F − − = − C. RSS ESS F = ; D. ESS RSS F = 15. 根据可决系数 R 2 与 F 统计量的关系可知，当 R 2=1 时有（ ）。 A. F=1； B. F=－1； C. F→+∞ ； D. F=0 16. 线性回归模型的参数估计量 b 是随机变量 Y 的函数，即 b = X X X Y −1 ( ) 。所以 b 是（ ）。 A. 随机变量； B. 非随机变量； C. 确定性变量； D. 常量 17. 由 Yf = X f b ˆ 可以得到被解释变量的估计值，由于模型中参数估计量的不确定性 及随机误差项的影响，可知 Yf ˆ 是（ ）。 A. 确定性变量； B. 非随机变量； C. 随机变量； D. 常量 18. 下面哪一表述是正确的（ ）。 A. 线性回归模型 Y =  0 + 1X + u 的零期望假设是指 0 1 1  = = n i ui n B. 对模型 Y =  0 + 1X1 +  2X2 + u 进行方程显著性检验（即 F 检验），检验的零 假设是 0 0 1 2 H : =  =  C. 相关系数较大意味着两个变量存在较强的因果关系 D. 当随机误差项的方差估计量等于零时，说明被解释变量与解释变量之间为函数关系

三、多选题 1下列哪些形式是正确的( A.Y=B。+BX;B.Y=B。+BX1+u;C.Y=b。+bX1+u D.Y=bo+bX+u;E.Y=bo+bX i F.EY)=B。+BX G.Y=b。+bX HY=b+bte I.F=bo+bX+e; J.EY)=b。+bX 2.调整后的多重可决系数2的正确表达式有( ）. A1-w-a-》 B1-0-ya-利 ∑-)n-k) ∑Y-)n-1) C1-1-R-l D.1-1-R2)n-k n-k n-1 E1-0+) 3.设k为回归模型中的参数个数（包括截距项），则总体线性回归模型进行显著性检 验时所用的F统计量可表示为( A∑0-n- B∑0-产k-D ∑e2《k-1) ∑e2n-k) R2k-) Ca-R)m-个 D.(1-R)/An-k).E R2/(n-k) R2k-1) (1-R2)k-1) 4.回归平方和∑2是指( A.被解释变量的观测值Y与其平均值了的离差平方和 B.被解释变量的回归值丫与其平均值了的离差平方和 C.被解释变量的总体平方和∑y2与残差平方和∑e2之差 D.解释变量变动所引起的被解释变量的离差的大小 E.随机因素影响所引起的被解释变量的离差大小 5.在多元线性回归分析中，修正的可决系数2与可决系数R之间(

三、多选题 1.下列哪些形式是正确的（ ）。 A. Y =  0 + 1X1 ; B. Y =  0 + 1X1 + u ； C. Y = b0 + b1X1 + u ; D. Y = b0 + b1X1 + u ˆ ； E. 0 1 1 Y ˆ = b + b X ; F. 0 1 1 E(Y) =  +  X G. Y = b0 + b1X1 ; H. Y = b + b X + e 0 1 1 ； I. Y = b + b X + e 0 1 1 ˆ ; J. 0 1 1 E(Y) = b + b X 2. 调整后的多重可决系数 2 R 的正确表达式有（ ）。 A.   − − − − − ) /( ) ˆ ( ( ) /( 1) 1 2 2 Y Y n k Y Y n ; B.   − − − − − ( ) /( 1) ) /( ) ˆ ( 1 2 2 Y Y n Y Y n k C. n k n R − − − − 1 1 (1 ) 2 ; D. 1 1 (1 ) 2 − − − − n n k R E. 1 1 (1 ) 2 − − − + n n k R 3. 设 k 为回归模型中的参数个数（包括截距项），则总体线性回归模型进行显著性检 验时所用的 F 统计量可表示为（ ）。 A.   − − − /( 1) ) /( ) ˆ ( 2 2 e k Y Y n k ; B.   − − − /( ) ) /( 1) ˆ ( 2 2 e n k Y Y k C. (1 )/( ) /( 1) 2 2 R n k R k − − − ; D. /( 1) (1 )/( ) 2 2 − − − R k R n k ; E. (1 )/( 1) /( ) 2 2 − − − R k R n k 4. 回归平方和  2 y ˆ 是指（ ）。 A. 被解释变量的观测值 Y 与其平均值 Y 的离差平方和 B. 被解释变量的回归值 Y ˆ 与其平均值 Y 的离差平方和 C. 被解释变量的总体平方和  2 y 与残差平方和  2 e 之差 D. 解释变量变动所引起的被解释变量的离差的大小 E. 随机因素影响所引起的被解释变量的离差大小 5. 在多元线性回归分析中，修正的可决系数 2 R 与可决系数 2 R 之间（ ）

AR2<R2;B.R2≥R2;C.R2只能大于零，D.R2可能为负值 6.由下列方程判断模型()属于变量呈线性，模型()属于系数呈线性，模 型()既属于变量呈线性又属于系数呈线性，模型( )既不属于变量呈线性也 不属于系数呈线性。 A.Y=R+月X+u; BY=B。+BnX+u c.nY=B。+BnX+u: D.Y=B。+B,(B2X)+u E.Y=B/BX+u: F.Y=1+B(1-XA)+u G.Y=B。+BX,+BX2+u 四、简答题 1.什么是相关分析(Correlation)? 2.什么是相关图(Correlation graph)? 3.什么是相关系数(Correlation coefficient)? 4.给定一元线性回归模型：Y-B。+BX,+4 （1)叙述模型的基本假定；（2)写出参数B,和B,的最小二乘估计公式；（3)说明 满足基本假定的最小二乘估计量的统计性质；（4)写出随机扰动项方差的无偏估计公式。 5.从经济学和数学两个角度说明计量经济学横型的理论方程中必须包含随机误差项。 6.非线性计量模型转化成线性模型数学处理方法。 7.最小二乖法和最大似然法的基本原理。 8.最小样本容量、满足基本要求的样本容量 9.拟合优度检验与方程显著性检验的区别与联系。 10.如何缩小被解释变量预测值的置信区间。 五、实践题 1.下表列出若千干对因果关系变量，对海一对变量，你认为它们之间的关系如何？是正 的、负的、还是无法确定？并说明理由

A. 2 R < 2 R ; B. 2 R ≥ 2 R ; C. 2 R 只能大于零; D. 2 R 可能为负值 6. 由下列方程判断模型（ ）属于变量呈线性，模型（ ）属于系数呈线性，模 型（ ）既属于变量呈线性又属于系数呈线性，模型（ ）既不属于变量呈线性也 不属于系数呈线性。 A．Y = + X + u 3 0 1 11   ; B. Y =  0 + 1 ln X1 + u C. ln Y =  0 + 1 ln X1 + u ; D. Y =  0 + 1 ( 2X1 ) + u E. Y =  0 / 1X1 + u ; F. Y = 1+ (1− X ) + u 1 0 1   G. Y =  0 + 1X1 +  2X2 + u 四、简答题 1.什么是相关分析（Correlation）？ 2.什么是相关图（Correlation graph）？ 3.什么是相关系数 (Correlation coefficient）？ 4. 给定一元线性回归模型： Y =  0 + 1X1 + u （1）叙述模型的基本假定；（2）写出参数  0 和 1 的最小二乘估计公式；（3）说明 满足基本假定的最小二乘估计量的统计性质；（4）写出随机扰动项方差的无偏估计公式。 5. 从经济学和数学两个角度说明计量经济学模型的理论方程中必须包含随机误差项。 6. 非线性计量模型转化成线性模型数学处理方法。 7. 最小二乘法和最大似然法的基本原理。 8. 最小样本容量、满足基本要求的样本容量。 9. 拟合优度检验与方程显著性检验的区别与联系。 10. 如何缩小被解释变量预测值的置信区间。 五、实践题 1．下表列出若干对因果关系变量。对每一对变量，你认为它们之间的关系如何？是正 的、负的、还是无法确定？并说明理由

Y X GNP 利率 个人储器 利率 小麦产出 降雨景 羊国国防开古 前苏联国防开古 法残胆早木垒打的次数 甘任葬 总统吉誉 仟职时间 学牛计量轻济学成结 甘统十学成绩 日木汽车的进口 美国人均国足收】 2.现代投资分析的特征线涉及如下回归方程：，=B+Bvm+山，；其中：r表示股 票或债券的收益率；rm表示有价证券的收益率（用市场指数表示，如标准普尔500指数）：。 表示时间。在投资分析中，B1被称为债券的安全系数B,是用来度量市场的风险程度的，即 市场的发展对公司的财产有何影响。依据1956~1976年间240个月的数据Fogler和Ganpathy 得到BM股票的回归方程；市场指数是在芝加哥大学建立的市场有价证券指数 =0018s +10 R2-0.4710 要求：(1)解释回归参数的意义：(2)如何解释R2？(3)安全系数>1的证券称为不 稳定证券，建立适当的零假设及备选假设，并用t检验进行检验（一5%， 3.某农产品试验产量Y(公斤/亩)和施肥量X(公斤/庙)7块地的数据资料汇总如下 ∑x=255,∑y=3050;∑x2=1217.71;∑Jy=8371.429;∑y=3122.857 后来发现遗漏的第八块地的数据：X。=20,Y。=400。 要求汇总全部8块地数据后分别用小代数解法和矩阵解法进行以下各项计算，并对计算 结果的经济意义和统计意义做简要的解释。 (1)该农产品试验产量对施肥量X(公斤亩)回归模型Y=B。+BX,+“进行估计. (2)对回归系数（斜率）进行统计假设检验，显著性水平为0.05。 （3)估计可决系数并进行统计假设检验，显著性水平为0.05。 (4)计算施肥量对该农产品产量的平均弹性

2. 现代投资分析的特征线涉及如下回归方程： t mt ut r =  0 + 1 r + ；其中：r 表示股 票或债券的收益率；rm表示有价证券的收益率（用市场指数表示，如标准普尔 500 指数）；t 表示时间。在投资分析中，β1 被称为债券的安全系数 β，是用来度量市场的风险程度的，即 市场的发展对公司的财产有何影响。依据1956~1976年间240个月的数据，Fogler 和Ganpathy 得到 IBM 股票的回归方程；市场指数是在芝加哥大学建立的市场有价证券指数： (0.3001) (0.0728) 0.7264 1.0598 mt rt = + r  0.4710 2 R = 要求：（1）解释回归参数的意义；（2）如何解释 R 2？（3）安全系数 β>1 的证券称为不 稳定证券，建立适当的零假设及备选假设，并用 t 检验进行检验（α=5%）。 3. 某农产品试验产量 Y （公斤/亩）和施肥量 X （公斤/亩）7 块地的数据资料汇总如下： X = 255, Y = 3050 ；  =1217.71 2 x ；  = 8371.429 2 y ； xy = 3122.857 后来发现遗漏的第八块地的数据： X8 = 20，Y8 = 400 。 要求汇总全部 8 块地数据后分别用小代数解法和矩阵解法进行以下各项计算，并对计算 结果的经济意义和统计意义做简要的解释。 （1）该农产品试验产量对施肥量 X（公斤/亩）回归模型 Y =  0 + 1X1 + u 进行估计。 （2）对回归系数（斜率）进行统计假设检验，显著性水平为 0.05。 （3）估计可决系数并进行统计假设检验，显著性水平为 0.05。 （4）计算施肥量对该农产品产量的平均弹性。 Y X GNP 利率 个人储蓄 利率 小麦产出 降雨量 美国国防开支 前苏联国防开支 棒球明星本垒打的次数 其年薪 总统声誉 任职时间 学生计量经济学成绩 其统计学成绩 日本汽车的进口量 美国人均国民收入

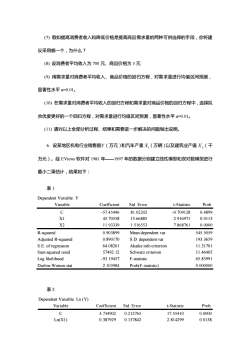
(5)令施肥量等于50公斤亩，对农产品试验亩产量进行预测，信度为0.05。 (6)冷施肥量等于30公斤庙，对农产品试验平均亩产量进行预测，显著性水平为0.01， 4.考虑以下预测的回归方程： ,=-120+0.10F+5.33S,R2=0.50 其中：y,为第t年的玉米产量（蒲式耳亩）：F为第t年的施肥强度（磅亩）；S,一 第1年的降雨量（英寸） 回答下列问题： (1)从F和5对Y的影响方面，说出本方程中系数0.10和5.33的含义： (2)常数项-120是否意味着玉米的负产量可能存在？ (3)假定B的真实值为0.40，则估计值是否有偏？为什么？ (4)假定该方程并不满足所有的古典模型假设，即并不是最佳线性无偏估计值，则是否 意味着Bs的真实值绝对不等于5,33？为什么？ 5.设某商品的需求量Y（百件)，消费者平均收入X,(百元)，该商品价格X2(元) 的统计数据如下：（至少保留三位小数) ∑y=800:∑X,=80:∑X2=60: ∑X,X,=439 ∑Y2=67450:∑X=740;∑X1=6920:∑X,=4500:n=10 经EViews计算部分结果如下：（表1、表2、表3中被解释变量均为Y,n=10) 表1 VARIABLE COEFFICIENT STD.ERROR T-STAT 2-TAILSIG 99469295 13472571 73830965 0000 2.5018954 0.7536147 3.3198600 0013 X2 -6.5807430 1.3759059 -4.78284360.002 R-squared 0.949336 Mean of dependent var 80.00000 Adjusted R-squared.94860 S.D.of dependent var 19.57890 S.E of regression 4.997021 Sum ofsquared resid 174.7915

（5） 令施肥量等于 50 公斤/亩，对农产品试验亩产量进行预测，信度为 0.05。 （6）令施肥量等于 30 公斤/亩，对农产品试验平均亩产量进行预测，显著性水平为 0.01。 4. 考虑以下预测的回归方程： Yt Ft 33RSt 120 0.10 5. ˆ = − + + 0.50 2 R = 其中： Yt 为第 t 年的玉米产量（蒲式耳/亩）； Ft 为第 t 年的施肥强度（磅/亩）； RSt —— 第 t 年的降雨量（英寸） 回答下列问题： （1）从 F 和 RS 对 Y 的影响方面，说出本方程中系数 0.10 和 5.33 的含义； （2）常数项 −120 是否意味着玉米的负产量可能存在？ （3）假定  F 的真实值为 0.40 ，则估计值是否有偏？为什么？ （4）假定该方程并不满足所有的古典模型假设，即并不是最佳线性无偏估计值，则是否 意味着  RS 的真实值绝对不等于 5.33 ？为什么？ 5. 设某商品的需求量 Y （百件），消费者平均收入 X1 （百元），该商品价格 X2 （元） 的统计数据如下： （至少保留三位小数） Y = 800 ; X1 = 80 ; X2 = 60 ; X1X2 = 439  = 67450 2 Y ;  = 740 2 X1 ;  = 6920 YX1 ; YX2 = 4500 ；n = 10 经 EViews 计算部分结果如下：（表 1、表 2、表 3 中被解释变量均为 Y , n = 10） 表 1 VARIABLE COEFFICIENT STD.ERROR T-STAT 2-TAILSIG C 99.469295 13.472571 7.3830965 0.000 X1 2.5018954 0.7536147 3.3198600 0.013 X2 - 6.5807430 1.3759059 - 4.7828436 0.002 R-squared 0.949336 Mean of dependent var 80.00000 Adjusted R- squared 0.934860 S.D. of dependent var 19.57890 S.E of regression 4.997021 Sum of squared resid 174.7915

Durbin-Watson stat 1.142593 F-statistics 65.58230 表2 VARIABLE COEFFICIENT STD ERROR T-STAT Prob 38.4000 8.3069248 4.622649 0.002 XI 5.200000 0.96566045.38491590.001 R-squared 0783768 Mean of dependent var 80.00000 Adjusted R-squared 0.756739 S.D.of dependent var 19.5789 S.E of regression 9.656604 Sum of squared resid 746.0000 Durbin-Watson stat 1.808472 F-statistics 28.99732 表3 VARIAbLe COEFFICIENT STD ERROR T-STAT Prob 140.0000 8.5513157 16371750 0000 X2 -10.00000 1.3693064 -7.3029674 0.000 R-squared 0869565 Mean of dependent var 8000000 Adjusted R-squared 0.853261 S.D.of dependent var 1957890 S.Eof regression 7.50000 Sum of squared resid 450.0000 Durbin-Watson stat 0.666667 F-statistics 53.33333 完成以下任务，并对结果进行简要的统计意义和经济意义解释（要求列出公式、代入数 据及计算结果，计算结果可以从上面直接引用)。 （1)建立需求量对消费者平均收入、商品价格的线性回归方程并进行估计 （2)对偏回归系数（斜率）进行检验，显著性水平=0.05。 （3)估计多重可决系数，以显著性水平-0.05对方程整体显著性进行检验。并估计校正 可决系数 （4)计算商品需求量分别与消费者平均收入和商品价格的偏相关系数。 (⑤)用Beta系数分析商品需求量对消费者平均收入的变化以及商品需求量对商品价格的 变化哪个更敏感， (6)需求量对收入的弹性以及需求量对价格的弹性分别是多少

Durbin-Watson stat 1.142593 F – statistics 65.58230 表 2 VARIABLE COEFFICIENT STD.ERROR T-STAT Prob. C 38.40000 8.3069248 4.6226493 0.002 X1 5.200000 0.9656604 5.3849159 0.001 R-squared 0.783768 Mean of dependent var 80.00000 Adjusted R- squared 0.756739 S.D. of dependent var 19.57890 S.E of regression 9.656604 Sum of squared resid 746.0000 Durbin-Watson stat 1.808472 F – statistics 28.99732 表 3 VARIABLE COEFFICIENT STD.ERROR T-STAT Prob. C 140.0000 8.5513157 16.371750 0.000 X2 - 10.00000 1.3693064 -7.3029674 0.000 R-squared 0.869565 Mean of dependent var 80.00000 Adjusted R- squared 0.853261 S.D. of dependent var 19.57890 S.E of regression 7.500000 Sum of squared resid 450.0000 Durbin-Watson stat 0.666667 F – statistics 53.33333 完成以下任务，并对结果进行简要的统计意义和经济意义解释（要求列出公式、代入数 据及计算结果，计算结果可以从上面直接引用）。 （1）建立需求量对消费者平均收入、商品价格的线性回归方程并进行估计。 （2）对偏回归系数(斜率)进行检验，显著性水平 α=0.05。 （3）估计多重可决系数，以显著性水平 α=0.05 对方程整体显著性进行检验。并估计校正 可决系数。 （4）计算商品需求量分别与消费者平均收入和商品价格的偏相关系数。 (5) 用 Beta 系数分析商品需求量对消费者平均收入的变化以及商品需求量对商品价格的 变化哪个更敏感。 (6) 需求量对收入的弹性以及需求量对价格的弹性分别是多少

(7)假如提高消费者收入和降低价格是提高商品需求量的两种可供选择的手段，你将建 议采用哪一个，为什么？ (8)设消费者平均收入为700元、商品价格为5元 (9,用需求量对消费者平均收入、商品价格的回归方程，对需求量进行均值区间预测， 显著性水平a-0.01, (10)在需求量对消费者平均收入的回归方程和需求量对商品价格的回归方程中，选择拟 合优度更好的一个回归方程，对需求量进行均值区间预测，显著性水平0.01， (11)请对以上全部分析过程、结果和需要进一步解决的问题做出说明。 6.设某地区机电行业销售额Y(万元)和汽车产量X,(万辆)以及建筑业产值X2(干 万元)。经EViews软件对1981年一1997年的数据分别建立线性模型和双对数模型进行 最小二乘估计，结果如下 表1 Dependent Variable:Y Variable Coefficient Std.Error t-Statistic Prob. -5745496 81.02202 -0.709128 0.4899 45.70558 15.6688 2.916971 0.0113 X2 11.93339 1.516553 7.868761 0.0000 R-squared 0.903899 Mean dependent var 545.5059 Adjusted R-squared 0.890170 S.D.dependent var 193.365 S.E.ofregression 64.08261 Akaike into criterion 11.31701 Sum squared resid 57492.12 Schwarzcriterion 11.46405 Log likelihood -9319457 E-statistic 65.83991 Durbin-Watson sta 2.103984 Prob(F-statistic) 0.000000 表2 Dependent Variable:Ln(Y) Variable Coefficient Std.Error t-Statistic Prob. n 37349020212765 1755410 00000 Ln(X1) 0.387929 0.137842 2.814299 0.0138

(7) 假如提高消费者收入和降低价格是提高商品需求量的两种可供选择的手段，你将建 议采用哪一个，为什么？ (8) 设消费者平均收入为 700 元、商品价格为 5 元 (9) 用需求量对消费者平均收入、商品价格的回归方程，对需求量进行均值区间预测， 显著性水平 α=0.01。 (10) 在需求量对消费者平均收入的回归方程和需求量对商品价格的回归方程中，选择拟 合优度更好的一个回归方程，对需求量进行均值区间预测，显著性水平 α=0.01。 (11) 请对以上全部分析过程、结果和需要进一步解决的问题做出说明。 6. 设某地区机电行业销售额 Y （万元）和汽车产量 X1 （万辆）以及建筑业产值 X2 （千 万元）。经 EViews 软件对 1981 年——1997 年的数据分别建立线性模型和双对数模型进行 最小二乘估计，结果如下： 表 1 Dependent Variable: Y Variable Coefficient Std. Error t-Statistic Prob. C -57.45496 81.02202 -0.709128 0.4899 X1 45.70558 15.66885 2.916971 0.0113 X2 11.93339 1.516553 7.868761 0.0000 R-squared 0.903899 Mean dependent var 545.5059 Adjusted R-squared 0.890170 S.D. dependent var 193.3659 S.E. of regression 64.08261 Akaike info criterion 11.31701 Sum squared resid 57492.12 Schwarz criterion 11.46405 Log likelihood -93.19457 F-statistic 65.83991 Durbin-Watson stat 2.103984 Prob(F-statistic) 0.000000 表 2 Dependent Variable: Ln (Y) Variable Coefficient Std. Error t-Statistic Prob. C 3.734902 0.212765 17.55410 0.0000 Ln(X1) 0.387929 0.137842 2.814299 0.0138