《计量经济学》课程教学课件（PPT讲稿）02 简单线性回归模型

中匣寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 第二章 简单线性回归模型

简单线性回归模型 第二章

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 学习要点 一、简单线性回归模型的设定 二、简单线性回归模型的基本假定 三、 简单线性回归模型参数的估计方法 四、参数估计量的统计性质 五、拟合优度的度量 六、回归条数的区间估计和假设检验 七、回归模型预测 入、EViews,应用

学习要点 一、简单线性回归模型的设定 二、简单线性回归模型的基本假定 三、简单线性回归模型参数的估计方法 四、参数估计量的统计性质 五、拟合优度的度量 六、回归系数的区间估计和假设检验 七、回归模型预测 八、EViews应用

中匣寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 一元线性回归模型 一 回归与相关关条 1.经济变量间的相互关条 ◆确定性的函数关系：Y=f(X) ◆不确定性的统计关系一相关关系 Y=f(X)+u(u为随机变量) ◆没有关系

1. 经济变量间的相互关系 ◆ 确定性的函数关系： ◆不确定性的统计关系—相关关系 (u为随机变量) ◆ 没有关系 （ 一）回归与相关关系 Y f X = ( ) Y = f (X) +u 一、一元线性回归模型

中虚寒笔大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 2.相关关系 ◆相关关系的描述 相关关系最直观的描述方式一坐标图（散布图） ◆相关关系的类型 从涉及的变量数量看： 简单相关、多重相关（复相关） 从变量相关关系的表现形式看：线 性相关一一散布图接近一条直线；非 线性相关一一散布图接近一条曲线。 从变量相关关系变化的方向看：正 相关一一变量同方向变化，同增同减： X 负相关一一变量反方向变化，一增 减；不相关

2.相关关系 ◆ 相关关系的描述 相关关系最直观的描述方式——坐标图（散布图） Y X • • • • • • • • • • ◆相关关系的类型 从 涉 及 的 变 量 数 量 看 ： 简单相关、多重相关（复相关） 从变量相关关系的表现形式看：线 性相关——散布图接近一条直线；非 线性相关——散布图接近一条曲线。 从变量相关关系变化的方向看：正 相关——变量同方向变化，同增同减； 负相关——变量反方向变化，一增一 减；不相关

中面寒笔大学红济管捏学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 3.相关程度的度量一简单相关系数 ∑(X-xY-) V∑x-x)2∑w-2 n∑W-∑x∑y Cov(X,Y) Vn∑x2-∑x)2][nr2-∑2]Var()var) ◆简单相关系数用来测度两个变量之间是否存在线性相关 关系，其变化范围在[-1,1]之间。越接近于-1，负相关 程度越高；越接近1，正相关程度越高。 ◆除过简单相关系数，还有偏相关系数、复相关系数来测 度变量间的相关关系，但是在含义上有差别

3.相关程度的度量—简单相关系数 Var( ) Var( ) Cov( , ) [ ( ) ][ ( ) ] ( ) ( ) ( )( ) 2 2 2 2 2 2 X Y X Y n X X n Y Y n XY X Y X X Y Y X X Y Y r X Y  = − − − = − − − − =           ◆ 简单相关系数用来测度两个变量之间是否存在线性相关 关系，其变化范围在 [-1，1] 之间。越接近于-1，负相关 程度越高；越接近1，正相关程度越高。 ◆ 除过简单相关系数，还有偏相关系数、复相关系数来测 度变量间的相关关系，但是在含义上有差别

中虚寒笔大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 使用相关华数时应注意 ◆X和Y都是相互对称的随机变量； ◆线性相关系数只反映变量间的线性相关程度，不能说明 非线性相关关系； ◆样本相关系数是总体相关系数的样本估计值，因抽样 波动，样本相关系数为随机变量，其统计显著性有待检验； ◆相关系数只能反映线性相关程度，不能确定因果关系，不 能说明相关关系具体接近娜条直线。 计量经济学关心：变量间的因果关系及隐藏在随机性后 面的统计规律性，这有赖于回归分析方法

◆ 和 都是相互对称的随机变量； ◆线性相关系数只反映变量间的线性相关程度，不能说明 非线性相关关系； ◆样本相关系数是总体相关系数的样本估计值，因抽样 波动，样本相关系数为随机变量，其统计显著性有待检验； ◆相关系数只能反映线性相关程度，不能确定因果关系，不 能说明相关关系具体接近哪条直线. 计量经济学关心：变量间的因果关系及隐藏在随机性后 面的统计规律性，这有赖于回归分析方法. 使用相关系数时应注意 X Y

中匣寒靠大学红济管视学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 4.回归分析 ◆ 回归的古典意义： 道尔顿遗传学的回归概念：父母身高与子女 身高的关系。 ◆回归的现代意义： 一个因变量对若干解释变量依存关系的研究。 ◆回归的目的（实质）： 由固定的解释变量去估计因变量的平均值

◆ 回归的古典意义： 道尔顿遗传学的回归概念： 父母身高与子女 身高的关系。 ◆ 回归的现代意义： 一个因变量对若干解释变量依存关系的研究。 ◆ 回归的目的（实质）： 由固定的解释变量去估计因变量的平均值。 4.回归分析

中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL (二)一元线性回归模型 1.一元线性回归模型设定 一元线性总体回归模型：Y=B。+B,X+u 一元线性总体回归函数：E(YX)=B+BX (Population Regression Function,PRF) 一元线性样本回归模型：Y=b,+b,X+e 一元线性样本回归函数：E(YX)=b,+bX (Sample Regression Function,SRF) 实际的经济研究中总体回归函数通常是未知的，只能根 据经济理论和实践经验去设定。“计量”的目的就是寻求 样本回归函数作为总体回归函数的估计

（二）一元线性回归模型 E(Y X) = 0 + 1 X Y = 0 + 1 X +u Y = b +b X + e 0 1 一元线性总体回归模型: 一元线性总体回归函数： （Population Regression Function, PRF) 一元线性样本回归模型： 一元线性样本回归函数： (Sample Regression Function, SRF) E(Y X) = b0 +b1 X 实际的经济研究中总体回归函数通常是未知的，只能根 据经济理论和实践经验去设定。“计量”的目的就是寻求 样本回归函数作为总体回归函数的估计。 1. 一元线性回归模型设定

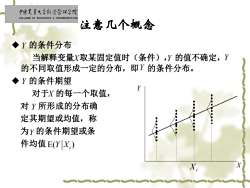
中慢寒靠大学红济管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL 注意几个概念 ◆Y的条件分布 当解释变量X取某固定值时（条件），Y的值不确定，Y 的不同取值形成一定的分布，即Y的条件分布。 ◆Y的条件期望 对于X的每一个取值， 对Y所形成的分布确 定其期望或均值，称 为y的条件期望或条 件均值E(YX,)

◆ 的条件分布 当解释变量 取某固定值时（条件）， 的值不确定， 的不同取值形成一定的分布，即 的条件分布。 ◆ 的条件期望 对于 的每一个取值， 对 所形成的分布确 定其期望或均值，称 为 的条件期望或条 件均值 注意几个概念 Xi X Y Y Y Y Y Y Y X Y X E( ) Y Xi

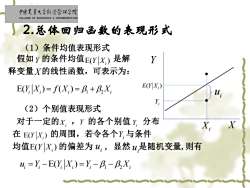
中面史靠大学红清管促学院 COLLEGE OF ECONOMICS MANAGEMENT.CAL )2.总体回归函数的表现形式 (1)条件均值表现形式 假如y的条件均值E(Yx)是解 释变量X的线性函数，可表示为： E(Y X)=f(X)=B+BX E(Y X,) (2)个别值表现形式 对于一定的x,y的各个别值y分布 X X 在EYx)的周围，若令各个Y,与条件 均值E(YX)的偏差为w,显然u,是随机变量，则有 u=Y-E(Y X)=Y-B-BX

• • i u Xi X Y ( ) E Y Xi Yi （1）条件均值表现形式 假如 的条件均值 是解 释变量 的线性函数，可表示为： （2）个别值表现形式 对于一定的 ， 的各个别值 分布 在 的周围，若令各个 与条件 均值 的偏差为 , 显然 是随机变量,则有 2.总体回归函数的表现形式 Xi E( ) Y Xi E( ) ( ) Y X f X X i i i i = = +   1 2 Yi E( ) Y Xi Yi E( ) Y Xi i u i u i i i i i i E( ) 1 2 u Y Y X Y X = − = − −   Y Y X