《热工基础》课程PPT教学课件（传热学）第三章 非稳态导热

第三章非稳态导热3-1 概述稳态导热：温度场不随时间变化：非稳态导热：温度场随时间而变化。分为周期性和瞬态两大类。前者物体内的温度场周期性地变化，后者物体的温度不断升高或降低。本章主要讨论瞬态非稳态导热过程非稳态导热物体的温度场可表示为：t = f(x,y,z,t)初始温度均匀并为t.的无限大平壁，突然投入到温度为t。的流体中对称加热。平壁中的温度分布、表面温度t和中心温度t的变化表面热流量的变化Φ如下图所示

第三章 非稳态导热 3-1 概述 ◆稳态导热：温度场不随时间变化； ◆非稳态导热：温度场随时间而变化。分为周期性和瞬态两 大类。前者物体内的温度场周期性地变化，后者物体的温 度不断升高或降低。本章主要讨论瞬态非稳态导热过程。 ◆非稳态导热物体的温度场可表示为： ◆一初始温度均匀并为t0的无限大平壁，突然投入到温度为 t∞的流体中对称加热。平壁中的温度分布、表面温度tw和 中心温度tm的变化表面热流量的变化Φ如下图所示。 t f x y z = ( , , , ) 

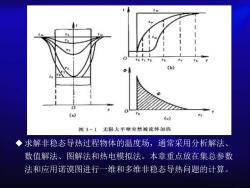
r(b)O(a)(e)图3-1无限人平吸奖然披流体加热求解非稳态导热过程物体的温度场，通常采用分析解法数值解法、图解法和热电模拟法。本章重点放在集总参数法和应用诺谟图进行一维和多维非稳态导热问题的计算

◆求解非稳态导热过程物体的温度场，通常采用分析解法、 数值解法、图解法和热电模拟法。本章重点放在集总参数 法和应用诺谟图进行一维和多维非稳态导热问题的计算

3-2集总参数法集总参数法：由于物体内温度相差不大，可近似认为在这种非稳态导热过程中物体内的温度分布于坐标无关，仅随时间变化，因此物体温度可用其任一点的温度表示，而将物体的质量和热容量等视为集中在这一点，这种方法叫做集总参数法。毕漏数：Bi=h_l内部导热热阻元外部（表面）传热热阻式中，1为引用尺寸。对于无限大平壁l=/2（半厚）对于无限长圆柱体和球le=d/2=R（半径）图3-2内部热阻可以忽略时平壁的对称加热

3-2 集总参数法 ◆ 集总参数法：由于物体内温度相差不大，可近似认为在这种非稳态导 热过程中物体内的温度分布于坐标无关，仅随时间变化，因此物体温 度可用其任一点的温度表示，而将物体的质量和热容量等视为集中在 这一点，这种方法叫做集总参数法。 ◆ 毕渥数： 内部导热热阻 外部（表面）传热热阻 式中，le为引用尺寸。 对于无限大平壁le =δ/2(半厚)； 对于无限长圆柱体和球le =d/2=R(半径) e e 1 s s hl l Bi   h = = =

符合集总参数法简化分析的物体非稳态导热的导热微分方程：pcv兴= h4(s。-1)dt变成齐次方程：pcv引入过余温度：=(t -t）=hAOdthA=exp(-分离变量并积分后得：pcV0。to-t.hAhl.at = B,.Fh(V / A) a/(pc)0111pcV元12(V/A)元式中，Bi和Fo统称为特征数，分别成为毕渥数和傅里叶数。脚标“V"表示特征尺寸，记作

◆ 符合集总参数法简化分析的物体非稳态导热的导热微分方程： 引入过余温度： 变成齐次方程： 分离变量并积分后得： 式中，Bi和Fo统称为特征数，分别成为毕渥数和傅里叶数。脚标“V”表 示特征尺寸，记作lc ( ) dt cV hA t t d   = −   ( ) t t = −  dt cV hA d    = 0 0 exp( ) t t hA t t cV       − = = − − 2 2 ( ) ( ) ( ) c iv ov c hA h V A c a hl B F cV V A l         = = =

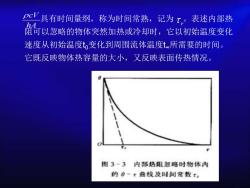
pcV具有时间量纲，称为时间常熟，记为t,。表述内部热阻可以忽略的物体突然加热或冷却时，它以初始温度变化速度从初始温度t.变化到周围流体温度t。所需要的时间。它既反映物体热容量的大小，又反映表面传热情况图3-3内部热阻急略时物体内的一：曲线及时间数t

具有时间量纲，称为时间常熟，记为 。表述内部热 阻可以忽略的物体突然加热或冷却时，它以初始温度变化 速度从初始温度t0变化到周围流体温度t∞所需要的时间。 它既反映物体热容量的大小，又反映表面传热情况。 cV hA  r 

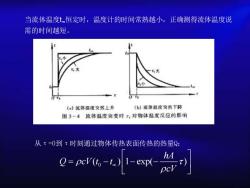
当流体温度t。恒定时，温度计的时间常熟越小，正确测得流体温度说需的时间越短。（b）流体度突然下降（）流体温度突然上升图3-4流体温度突变时，对物体温度反应的影响从T=0到T时刻通过物体传热表面传热的热量Q：nAQ= pcV(to -t.) 1-exp(-Oc

当流体温度t∞恒定时，温度计的时间常熟越小，正确测得流体温度说 需的时间越短。 从τ=0到τ时刻通过物体传热表面传热的热量Q： 0 ( ) 1 exp( ) hA Q cV t t cV       = − − −    

Q。=pcV(t。-t。），称为物体的初始过余恰，单位为J,它表示物体由初始温度t.变为环境（即流体）温度t。时吸收或放出的热量

，称为物体的初始过余焓，单位为J， 它表示物体由初始温度t0变为环境（即流体）温度t∞时吸 收或放出的热量。 0 0 Q cV t t  ( ) = − 

3-3内部热阻不可忽略的物体在第三类边界条件下的非稳态导热和诺谟图无限大平壁的分析解和诺谟图设有一厚21、无内热源地无限大平壁，初始温度均匀且为t.突然将其投放到温度为t。（恒定）的流体中加热（或冷却），表面传热系数为h（均匀、恒定）。无限大平壁两侧表面对称加热，中心面为对称面。Otat导热微分方程：Eaat-aax?h,to初始条件：T=0时，t(x,t)=toh,toJ边界条件：Ot(x,t).+x=0处，2=0 (对称性)Oxx=/ 处, h[(x,t)-t ]=-,0(x,)图3-5无限大平壁在第三类ax边界条件下的传热

3-3 内部热阻不可忽略的物体在第三类边界 条件下的非稳态导热和诺谟图 ◆ 无限大平壁的分析解和诺谟图 设有一厚2l、无内热源地无限大平壁，初始温度均匀且为t0突然将其投 放到温度为t∞(恒定) 的流体中加热(或冷却)，表面传热系数为h(均匀、 恒定)。无限大平壁两侧表面对称加热，中心面为对称面。 导热微分方程： 初始条件： 时， 边界条件： 处， (对称性) 处， 2 2 t t a  x   =   x = 0  = 0 0 t x t ( , )  = ( , ) 0 t x x   =  x l =   ( , ) ( , ) t x h t x t x      − = − 

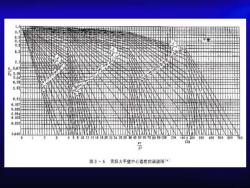
0.8o.0.o.8, 0.078:86.030.020.00000.0058:830.0030.A01101214161820222426283640506070857510012040050600700140J200300150兴图3-6无限大平整中心温度的诺谈

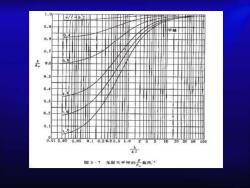
1.000.90.0.80.7i0.56.50.40.30.20.10.010.020.050.10.2030.51.0210203050100X因3-7无限大半账的一曲线*