《工程热力学》课程教学资源（例题讲解）第4章 理想气体热力过程及气体压缩

工程热力学例题高习瓶第4章理想气体热力过程及气体压缩41本章基本要求熟练掌握定容、定压、定温、绝热、多变过程中状态参数P、V、T、△U、△h、△s的计算，过程量Q、W的计算，以及上述过程在p-V、T-s图上的表示。4.2本章重点结合热力学第一定律，计算四个基本热力过程、多变过程中的状态参数和过程参数及在p-V、T-s图上表示。本章的学习应以多做练习题为主，并一定注意要在求出结果后，在p-V、T-s图上进行检验。4.3例题例1.2kg空气分别经过定温膨胀和绝热膨胀的可逆过程，如图4.1，从初态p,=9.807bar，t=300°C膨胀到终态容积为初态容积的5倍，试计算不同过程中空气的终态参数，对外所做的功和交换的热量以及过程中内能、烩、炳的变化量。Pt图4.1解：将空气取作闭口系对可逆定温过程1-2，由过程中的参数关系，得=9.807=1.961barP2 = Pr542—30—

工程热力学例题与习题 —30— 第 4 章 理想气体热力过程及气体压缩 4．1 本章基本要求 熟练掌握定容、定压、定温、绝热、多变过程中状态参数 p、v、T、 u、  h、  s 的计算，过程量 Q、W 的计算，以及上述过程在 p-v 、T-s 图 上的表示。 4．2 本章重点 结合热力学第一定律，计算四个基本热力过程、多变过程中的状态参 数和过程参数及在 p-v 、T-s 图上表示。本章的学习应以多做练习题为主， 并一定注意要在求出结果后，在 p-v 、T-s 图上进行检验。 4．3 例 题 例 1．2kg 空气分别经过定温膨胀和绝热膨胀的可逆过程，如图 4.1， 从初态 1 p =9.807bar, 1 t =300 C  膨胀到终态容积为初态容积的 5 倍，试计算 不同过程中空气的终态参数，对外所做的功和交换的热量以及过程中内能、 焓、熵的变化量。 图 4.1 解：将空气取作闭口系 对可逆定温过程 1-2，由过程中的参数关系，得 bar v v p p 1.961 5 1 9.807 2 1 2 = 1 =  =

工程热力学房题海可题RT, =0. 1677 m / kg按理想气体状态方程，得：PlV2 = 5v,=0. 8385 m / kgT, =T=573Kt2=300°C气体对外作的膨胀功及交换的热量为V2=529.4kJW,=Or=pVn-Vi过程中内能、焰、摘的变化量为AHi,=0 ~AS),==0. 9239kJ /KAU12=0T或AS),=mR1n=0. 9238kJ /KVi对可逆绝热过程1-2，由可逆绝热过程参数间关系可得pz = pi(一L)4其中v=vz=0.8385m/kgV2)14=1.03bar故P,=9.807(5T, =P=301Kf, =28°CR气体对外所做的功及交换的热量为11W. =-(p,V-P2V2)=-mR(T,-T,)=390.3kJk-1k-1Q, =0过程中内能、、熵的变化量为AU12 = mc,(T: -T)= -390.1kJ或△U1=-W,=-390.3kJAH,2 =mc,(T, -T)=-546.2kJAS..=(例2.1kg空气多变过程中吸取41.87kJ的热量时，将使其容积增大—31-

工程热力学例题与习题 —31— 按理想气体状态方程，得 1 1 1 p RT v = =0.1677 m / kg 3 2 5 1 v = v =0.8385 m / kg 3 T2 = T1 =573K 2 t =300 C  气体对外作的膨胀功及交换的热量为 1 2 1 1 ln V V WT = QT = p V =529.4kJ 过程中内能、焓、熵的变化量为 U12 =0 H12 =0 S12 = T1 QT =0.9239kJ /K 或 S12 =mRln 1 2 V V =0.9238kJ /K 对可逆绝热过程 1-2′, 由可逆绝热过程参数间关系可得 k v v p p ( ) 2 1 1 ' 2 = 其中 2 ' 2 v = v =0.8385 m / kg 3 故 1.4 2 ) 5 1 p ' = 9.807( =1.03bar R p v T ' ' ' 2 2 2 = =301K ' 2 t =28 C  气体对外所做的功及交换的热量为 ( ) 1 1 ( ) 1 1 ' 1 1 2 2 1 2 mR T T k p V p V k Ws − − − = − = =390.3kJ ' = 0 s Q 过程中内能、焓、熵的变化量为 U mc T T k J v ( 1 ) 390.1 12 2  ' = ' − = − 或 U W 390.3kJ  12 ' = − 2 = − H mc T T kJ p ( 1 ) 546.2 12 2  ' = ' − = − ' 12 S =0 例 2. 1kg 空气多变过程中吸取 41.87kJ 的热量时，将使其容积增大

工程热力学房题海可题10倍，压力降低8倍，求：过程中空气的内能变化量，空气对外所做的膨胀功及技术功。1解：按题意q，=41.87kJ/kgVz=10vP2=Sp空气的内能变化量：由理想气体的状态方程pV = RTPV, = RT,10TT, =得：8In(p, / p2) n8多变指数0.903n:n10In(v, /v)多变过程中气体吸取的热量q,=c,(T,-T)=c, n-k(n-k(T, -T)=-C.n-1n-T = 57.1K气体内能的变化量AU12=mc,(T,-T)=8.16kJ/kg空气对外所做的膨胀功及技术功：膨胀功由闭系能量方程Wi2=qn-Au12=33.71kJ/kg1RT,[1-()1来计算或由公式W12=n-1Pi1-nRT,[1-(P2)- ]= mwi2 = 30.49kJ / g技术功：W12=n-1Pi例3：一气缸活塞装置如图4.2所示，气缸及活塞均由理想绝热材料组成，活塞与气缸间无摩擦。开始时活塞将气缸分为A、B两个相等的两部分，两部分中各有1kmol的同一种理想气，其压力和温度均为p=1bar，ti=5℃。若对A(BA中的气体缓慢加热（电热），使气体缓慢膨胀，推动活塞压缩B中的气体，直至A中气图4.2—32-

工程热力学例题与习题 —32— 10 倍，压力降低 8 倍，求：过程中空气的内能变化量，空气对外所做的膨 胀功及技术功。 解：按题意 qn = 41.87kJ / kg 2 10 1 v = v 2 1 5 1 p = p 空气的内能变化量：由理想气体的状态方程 p1V1 = RT1 p2V2 = RT2 得： 2 1 8 10 T = T 多变指数 0.903 ln10 ln 8 ln( / ) ln( / ) 2 1 1 2 = = = v v p p n 多变过程中气体吸取的热量 2 1 2 1 1 4 1 1 ( ) 1 ( ) T n n k T T c n n k q c T T c n n v v − − − = − − = − = T1 = 57.1K 气体内能的变化量 U12 = mcv (T2 −T1 ) = 8.16kJ / kg 空气对外所做的膨胀功及技术功：膨胀功由闭系能量方程 w12 = qn − u12 = 33.71kJ / kg 或由公式 [1 ( ) ] 1 1 1 1 2 12 1 n n p p RT n w − − − = 来计算 技术功： nw k J k g p p RT n n w n n [1 ( ) ] 30.49 / 1 12 1 1 2 12 1 − = = − = − 例 3：一气缸活塞装置如图 4.2 所示，气缸及活塞均由理想绝热材料 组成，活塞与气缸间无摩擦。开始时活塞将气缸分为 A、B 两个相等的两部 分，两部分中各有 1kmol 的同一种理想气， 其压力和温度均为 p1=1bar，t1=5℃。若对 A 中的气体缓慢加热（电热），使气体缓慢膨 胀，推动活塞压缩 B 中的气体，直至 A 中气 A B 图 4.2

工程热力学例题房习题体温度升高至127℃。试求过程中B气体吸取的热量。设气体Cro=12.56kJ/(kmol·K)，Cpo=12.56kJ/(kmol·K）。气缸与活塞的热容量可以忽略不计。解：取整个气缸内气体为闭系。按闭系能量方程AQ-W因为没有系统之外的力使其移动，所以0则Q=AU=AUA+AU=nCAT+nCAT其中ng=ng=1kmol故(1)Q=Cro(AT +AT)在该方程△T中是已知的，即△T,=TA2-TA=TA2-T。只有△T是未知量。当向A中气体加热时，A中气体的温度和压力将升高，并发生膨胀推动活塞右移，使B的气体受到压缩。因为气缸和活塞都是不导热的，而且其热容量可以忽略不计，所以B中气体进行的是绝热过程。文因为活塞与气缸壁间无摩擦，而且过程是缓慢进行的，所以B中气体进行是可逆绝热压缩过程。按理想气体可逆绝热过程参数间关系k-1TB2P2T,P(2)由理想气体状态方程，得V=(mA+n,)RM初态时PiV, = (nRuTa +ngRuTm)终态时P2其中V和V是过程初，终态气体的总容积，即气缸的容积，其在过程前后不变，故V=V2，得33

工程热力学例题与习题 —33— 体温度升高至 127 ℃。试求过程中 B 气体吸取的热量。设气体 Cv0 = 12.56 kJ/(kmol·K)， Cp0 = 12.56 kJ/(kmol·K)。气缸与活塞的热容 量可以忽略不计。 解：取整个气缸内气体为闭系。按闭系能量方程 ΔU=Q－W 因为没有系统之外的力使其移动，所以 W=0 则 Q = U = UA + UB = nACv0TA + nBCv0TB 其中 nA = nB =1 kmol 故 ( ) Q = Cv0 TA + TB （1） 在该方程 TA 中是已知的，即 TA = TA2 −TA1 = TA2 −T1 。只有 TB 是未 知量。 当向 A 中气体加热时，A 中气体的温度和压力将升高，并发生膨胀推 动活塞右移，使 B 的气体受到压缩。因为气缸和活塞都是不导热的，而且 其热容量可以忽略不计，所以 B 中气体进行的是绝热过程。又因为活塞与 气缸壁间无摩擦，而且过程是缓慢进行的，所以 B 中气体进行是可逆绝热 压缩过程。 按理想气体可逆绝热过程参数间关系 k k B p p T T 1 1 2 1 2 −         = （2） 由理想气体状态方程，得 初态时 1 1 1 ( ) p n n R T V A + B M = 终态时 2 2 2 2 ( ) p n R T n R T V A M A + B M B = 其中 V1和 V2是过程初，终态气体的总容积，即气缸的容积，其在过程前后 不变，故 V1=V2，得

工程热力学房题海习题(nA+ng)RMT_(nRMTA2+ngRMTB2)P2P3因为na=n=1kmolp2T42+ TB2所以(3)21T,T(P合并式（2）与（3），得k-1P2P2nn.比值卫可用试算法求用得。Pi按题意已知：T42=273+172=445K，T=273+5=278KCro12.56k-110.40=kkCpo20.880.4445P2P故278p,pP2 =1.367计算得：Pi代式入（2）得-= 278×(1.367)0.4 = 315KD.代入式（1）得Q=12.56[(445—278)+(315—278)]=2562kJ例4：2kg的气体从初态按多变过程膨胀到原来的3倍，温度从300℃下降至60℃，已知该过程膨胀功为100kJ自外界吸热20kJ，求气体的c,和c各是多少？现列出两种解法：—34-

工程热力学例题与习题 —34— 2 2 2 3 3 ( ) ( ) p n R T n R T p nA nB RM T A M A + B M B = + 因为 nA = nB =1 kmol 所以 1 2 1 2 1 2 2 T T T T p p A B = +         （3） 合并式（2）与（3），得 k k A p p T T p p 1 1 2 1 2 1 2 2 −         = +         比值 1 2 p p 可用试算法求用得。 按题意已知： T A2= 273+172 =445K，T1= 273+ 5 =278K 0.40 20.88 12.56 1 1 1 1 1 0 = − = − = − = − p vo C C k k k 故 0.4 1 2 1 2 278 445 2         = +         p p p p 计算得： 1 2 p p =1.367 代式入（2）得 278 1.367 315K 0.4 1 1 2 2 1 =  =         = − （ ） k k B p p T T 代入式（1）得 Q=12.56[(445－278)+(315－278)]=2562kJ 例 4：2kg 的气体从初态按多变过程膨胀到原来的 3 倍，温度从 300℃ 下降至 60℃，已知该过程膨胀功为 100kJ 自外界吸热 20kJ，求气体的 cp 和 cv各是多少？ 现列出两种解法：

工程热力学例题习画解1：由题已知：V=3V(μ)~1由多变过程状态方程式=7(v)T.hT,即n-l:hiVT60+273In InT,300+273+1=1.494+1:n=Imln!3V由多变过程计算功公式：1W=m-R(T -T)=100kJn-1W(n-1)100(1.494-1)故R=.m(T-T,)2(573-333)=0.1029kJ/kg·K式中C,=c,-R=k·c-RR代入热量公式得C,k-1n-kR21.494-k0.1029(333-573)=20kJ(T, -T)=2xO=mn-1 k-11.494-1k-1得k=1.6175R0.1029.:.0.1666kJ/kg·KC.:k-1 1.6175-1c,=cv·k=0.1666×1.6175=0.2695kJ/kg·K解2：用解1中同样的方法求同=1.494R=0.1029kJ/kg·K由AU = mc,(T, -T)—35—

工程热力学例题与习题 —35— 解 1：由题已知：V1=3V2 由多变过程状态方程式 1 2 1 1 2 −         = n V V T T 即 1 2 1 2 ln ln 1 V V T T n − = 1 1.494 3 1 ln 300 273 60 273 ln 1 ln 1 2 1 2 + =       + + = + = V V lm T T n 由多变过程计算功公式： ( ) 100kJ 1 1 1 − 2 = − = R T T n W m 故 2(573 333) 100(1.494 1) ( ) ( 1) 1 2 − − = − − = m T T W n R =0.1029kJ/kg·K 式中 cv = c p − R = k  cv − R 得 −1 = k R cv 代入热量公式 (333 573) 20kJ 1 0.1029 1.494 1 1.494 ( ) 2 1 1 2 1 − = −  − − − =  −  − − = k k T T k R n n k Q m 得 k=1.6175 ∴ 0.1666kJ/kg K 1.6175 1 0.1029 1 =  − = − = k R cv cp=cv·k=0.1666×1.6175=0.2695kJ/kg·K 解 2：用解 1 中同样的方法求同 n=1.494 R=0.1029kJ/kg·K 由 ( ) U = mcv T2 −T1

工程热力学房题海习题即Q-W =mc,(T, -T)O-w=C..m(T, -T,)20-100得2(333573)= 0.167kJ/kg-KCp =c,+R=0.167+0.1029=0.2695kJ/kgK例5：1kg空气分两种情况进行热力过程，作膨胀功300kJ。一种情况下吸热380kJ，另一情况下吸热210kJ。问两种情况下空气的内能变化多少？若两个过程都是多变过程，求多变指数，并将两个过程画在同一张PV图上。按定比热容进行计算。解：（1）求两个过程的内能变化。两过程内能变化分别为：Au,=qi-w,=380-300=80kJ/kgAuz =q2-wz =210-300=-90kJ/kg（2）求多变指数。80Au,△T, ==111.6K0.717c,Auz- 90AT,-125K0.717c,1因为RATW1-n所以，两过程的多变指数分别为：R(△T)0.287×111.6=0.89n, =1-300WiR(AT)2 =1-0.287×(-125) =1.12n, =1-300W2（3）两多变过程p-v图T-s图如图4.3所示。—36-

工程热力学例题与习题 —36— 即 ( ) Q −W = mcv T2 −T1 得 0.167kJ/kg K 2(333 573) 20 100 ( ) 2 1 =  − − = − − = m T T Q W cv 0.2695kJ/kg K 0.167 0.1029 =  = + c p = cv + R 例 5：1kg 空气分两种情况进行热力过程，作膨胀功 300kJ。一种情况 下吸热 380kJ，另一情况下吸热 210kJ。问两种情况下空气的内能变化多 少？若两个过程都是多变过程，求多变指数，并将两个过程画在同一张 p-v 图上。按定比热容进行计算。 解：（1）求两个过程的内能变化。 两过程内能变化分别为： u1 = q1 −w1 = 380 −300 = 80kJ/kg u2 = q2 −w2 = 210 −300 = −90kJ/kg （2）求多变指数。 111.6K 0.717 1 80 1 = =   = v c u T 125K 0.717 2 90 2 = − − =   = v c u T 因为 R T n w  − = 1 1 所以，两过程的多变指数分别为： 0.89 300 0.287 111.6 1 ( ) 1 1 1 1 =  = −  = − w R T n 1.12 300 0.287 ( 125) 1 ( ) 1 2 2 2 =  − = −  = − w R T n （3）两多变过程 p-v 图 T-s 图如图 4.3 所示

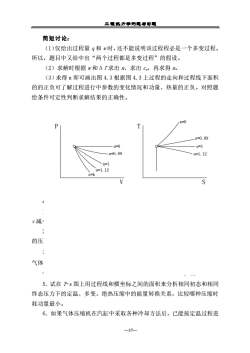
工程热力学房题高可题简短讨论：（1）仅给出过程量g和w时，还不能说明该过程程必是一个多变过程。所以，题目中又给中出“两个过程都是多变过程”的假设。（2）求解时根据w和△T求出n，求出Cp，再求得n。（3）求得n即可画出图4.3根据图4.3上过程的走向和过程线下面积的的正负可了解过程进行中参数的变化情况和功量、热量的正负。对照题给条件可定性判断求解结果的正确性。1-0PTn=0.89n=0n=1n=0.89n=1. 12n=)n=1. 12n=ksVv减的压M-气体25.试在T-s图上用过程线和横坐标之间的面积来分析相同初态和相同终态压力下的定温、多变、绝热压缩中的能量转换关系，比较哪种压缩时耗功量最小。6.如果气体压缩机在汽缸中采取各种冷却方法后，已能按定温过程进37

工程热力学例题与习题 —37— 简短讨论： （1）仅给出过程量 q 和 w 时，还不能说明该过程程必是一个多变过程。 所以，题目中又给中出“两个过程都是多变过程”的假设。 （2）求解时根据 w 和ΔT 求出 n，求出 cp，再求得 n。 （3）求得 n 即可画出图 4.3 根据图 4.3 上过程的走向和过程线下面积 的的正负可了解过程进行中参数的变化情况和功量、热量的正负。对照题 给条件可定性判断求解结果的正确性。 图 4.3 4．4 思考及练习题 1．在 p-v 图上，T 和 s 减小的方向分别在哪个方向，在 T-s 图上 p 和 v 减小的方向分别在哪个方向。 2．工质为空气，试在 p-v 和 T-s 图上画出 n=1.5 的膨胀过程和 n=1.2 的压缩过程的大概位置，并分析二过程中 q、w、 u 的正负。 3．如果气体按 v = c / p 规律膨胀，其中 c 为常数，则此过程中理想 气体被加热还是被冷却。 4．在多变过程中热量和功量之间的关系等于什么，即 wn qn / =? 5．试在 T-s 图上用过程线和横坐标之间的面积来分析相同初态和相同 终态压力下的定温、多变、绝热压缩中的能量转换关系，比较哪种压缩时 耗功量最小。 6．如果气体压缩机在汽缸中采取各种冷却方法后，已能按定温过程进 S n=1 n=1.12 n=k V n=1.12 n=0.89 P n=1 n=0 T n=0 n=0.89 图 4.3

工程热力学例题高习瓶行压缩，这时是否还要采用分级压缩，为什么。7.在常压下对3kg水加热，使水温由25°C升到95°C，设环境温度为15°C，求水吸收热量的可用能为多少，若将95°C的3kg水与20°C的2kg水混合，求混合过程中的可用能损失8.一台两级空气压缩机，进口流量为10m3/min，压力从1bar升高到1.5bar，如压缩轴功为最小，则中间压力为多少，如rF1.3，求两级压缩比单级压缩所节约的轴功9.容器被闸门分成两部分，A中气体参数为P、T，B为真空。现将隔板抽去，气体作绝热自由膨胀，终压降为P2。试问终了温度Tz是否可用下式计算？为什么？T, =T10，一绝热刚体容器，用隔板分成两部分，左边为高压气体，右边为真空，抽去隔板时，气体立即充满整个容器，问工质内能、温度如何变化，如该刚体容器是绝对导热的，则工质内能，温度又如何变化？11.如图4.4所示，9ABc与qADc谁大T24C图 4. 4图 4.512.如图4.5所示，9234与9214谁大，W234与W214谁大13.试比较图4.6中所示的循环1—2—3—4—1与卡诺循环1—2—3'一4一1的热效率，并讨论上述比较结果与“卡诺循环热效率最高”这一结论是否矛盾。14.导出循环1—2—3—1与循环1—2—3—1（见图4.7）的热效率的计算（以T、T为变量）。38

工程热力学例题与习题 —38— 行压缩，这时是否还要采用分级压缩，为什么。 7．在常压下对 3kg 水加热，使水温由 25 C  升到 95 C  ，设环境温度 为 15 C  ,求水吸收热量的可用能为多少，若将 95 C  的 3kg 水与 20 C  的 2kg 水混合，求混合过程中的可用能损失 8．一台两级空气压缩机，进口流量为 10 3 m /min，压力从 1bar 升高到 1.5bar，如压缩轴功为最小，则中间压力为多少，如 n=1.3 , 求两级压缩 比单级压缩所节约的轴功。 9．容器被闸门分成两部分，A 中气体参数为 PA、TA，B 为真空。现将 隔板抽去，气体作绝热自由膨胀，终压降为 P2。试问终了温度 T2是否可用 下式计算？为什么？   1 1 2 2 −         = p p T TA 10．一绝热刚体容器，用隔板分成两部分，左边为高压气体，右边为 真空，抽去隔板时，气体立即充满整个容器，问工质内能、温度如何变化， 如该刚体容器是绝对导热的，则工质内能，温度又如何变化？ 11．如图 4.4 所示， qABC 与 qADC 谁大 图 4.4 图 4.5 12．如图 4.5 所示， 234 q 与 q214 谁大， w234 与 w214 谁大 13．试比较图 4.6 中所示的循环 1—2—3—4—1 与卡诺循环 1—2— 3—4—1 的热效率，并讨论上述比较结果与“卡诺循环热效率最高”这一 结论是否矛盾。 14．导出循环 1—2—3—1 与循环 1—2 —3—1（见图 4.7）的热效率 的计算（以 T1、T2为变量）

工程热力学房题海习题15.设有卡诺循环1—2—3—4—1与实际循环1—2—3—4'—1，见图4.8。实际循环中，1一2'所示的绝热理膨胀过程，3一4'为实际的绝热压缩过程。试证明：对于卡诺循环=0T对于实际循环d2<0TTL22Ti-1T241ss后烩中止拿18.377J（kg·K），k=1.25的理想气体1.36kg，从p=551.6kPa，t=60℃C经定容过程达到p=1655kPa。过程中除了以搅拌器搅动气体外，还加入热量105.5kJ。求：（1）终态温度t2；（2）经搅拌器输入的功量：（3）气体内能的变化：—39—

工程热力学例题与习题 —39— 15．设有卡诺循环 1—2—3—4—1 与实际循环 1—2 —3—4 —1，见 图 4.8。实际循环中，1—2 所示的绝热理膨胀过程，3— 4 为实际的绝热 压缩过程。 试证明：对于卡诺循环  = 0 T dQ 对于实际循环  T dQ ＜0 图 4.6 图 4.7 图 4.8 16．0.4kg 空气，在 p1=1.98bar，t1=300℃下等温膨胀到 v2=1.68m3 /kg， 后经等压压缩，再在等容下加热使其回到初态，求每一过程中内能的变化， 焓的变化和所作的功，并求出各状态点的 p、v、T 值。在 p—v 和 T—s 图 中表示出各过程线来。 17．一定质量的空气初始为 25℃，压力为 6.85bar，容积为 0.02m3， 此空气先在定压下膨胀至 0.08m3，然后按 n=1.5 的多变过程膨胀，并由一 等温过程完成一个循环，此循环中所有过程是可逆的。 ①将此三个过程画在 p—v 图上，并求出各状态点的 p、v、T 值。 ②求出这些过程中的功量和热量。 18．R=377J(kg·K)，k=1.25 的理想气体 1.36kg，从 p1=551.6kPa，t1=60 ℃经定容过程达到 p1=1655kPa。过程中除了以搅拌器搅动气体外，还加入 热量 105.5kJ。求： （1）终态温度 t2； （2）经搅拌器输入的功量； （3）气体内能的变化； 1 1' 2 3 3' 4 1 3 2 2' L S T T 2 1 T S 3 2 2' 1 4 4