《工程热力学》课程教学资源（例题讲解）第5章 热力学第二定律

工程热力学例题与习题第5章热力学第二定律5.1本章基本要求理解热力学第二定律的实质，卡诺循环，卡诺定理，孤立系统炳增原理，深刻理解炳的定义式及其物理意义。熟练应用炳方程，计算任意过程炳的变化，以及作功能力损失的计算，了解炕的概念。5.2本章重点：学习本章应该掌握以下重点内容：1：深入理解热力学第二定律的实质，它的必要性。它揭示的是代么样的规律；它的作用。2.深入理解摘参数。为什么要引入熵。是在什么基础上引出的。怎样引出的。它有什么特点。3.系统摘变的构成，熵产的意义，熟练地掌握熵变的计算方法。4.深入理解摘增原理，并掌握其应用5，深入理解能量的可用性，掌握作功能力损失的计算方法5.3本章难点1，过程不可逆性的理解，过程不可逆性的含义。不可逆性和过程的方向性与能量可用性的关系。2.状态参数熵与过程不可逆的关系。3.熵增原理的应用。4.不可逆性的分析和分析5.4例题例1：空气从P=0.1MPa，t=20℃，经绝热压缩至P=0.42MPa，t=200℃。求：压缩过程工质摘变。（设比热为定值）。ZR=7解：定压比热：Cp=×0.287=1.005kJ/kg.k22-44

工程热力学例题与习题 —44— 第 5 章 热力学第二定律 5．1 本章基本要求 理解热力学第二定律的实质，卡诺循环，卡诺定理，孤立系统熵增原理， 深刻理解熵的定义式及其物理意义。 熟练应用熵方程，计算任意过程熵的变化，以及作功能力损失的计算， 了解火用、火无 的概念。 5．2 本章重点: 学习本章应该掌握以下重点内容:, l．深入理解热力学第二定律的实质，它的必要性。它揭示的是什么样的 规律；它的作用。 2．深入理解熵参数。为什么要引入熵。是在什么基础上引出的。怎样引 出的。它有什么特点。 3．系统熵变的构成，熵产的意义，熟练地掌握熵变的计算方法。 4．深入理解熵增原理,并掌握其应用。 5．深入理解能量的可用性，掌握作功能力损失的计算方法 5．3 本章难点 l．过程不可逆性的理解，过程不可逆性的含义。不可逆性和过程的方向 性与能量可用性的关系。 2．状态参数熵与过程不可逆的关系。 3．熵增原理的应用。 4．不可逆性的分析和火用 分析. 5．4 例题 例 1：空气从 P1=0.1MPa，t1=20℃，经绝热压缩至 P2=0.42MPa，t2=200℃。 求：压缩过程工质熵变。（设比热为定值）。 解：定压比热： C R k J k g k P = =  0.287 =1.005 /  2 7 2 7

工程热力学例题与习题由理想气体熵的计算式：-Rin=1.005mn0.287n2=0.069kJ/kgASi2 =C, n 2930.1TRP例2：刚性容器中贮有空气2kg，初态参数P=0.1MPa，T=293K，内装搅拌器，输入轴功率W=0.2kW，而通过容器壁向环境放热速率为O=0.1kW。求：工作1小时后孤立系统焰增。解：取刚性容器中空气为系统，由闭系能量方程：W，=Q+AU经1小时，3600W,=3600Q+mC.(T,-T)3600|w-3600(0.2-0.1)=293+2=544KT, =T+mC,2×0.7175B=RE544P2_T2.2=0.1x由定容过程：=0.186MPaPTT293取以上系统及相关外界构成孤立系统：ASise=AS+SsuASm-3600=12287kJ/K293T。ASiso=0.8906+1.2287=2.12kJ/K例3：压气机空气由P=100kPa，T=400K，定温压缩到终态P=1000kPa，过程中实际消耗功比可逆定温压缩消耗轴功多25%。设环境温度为T=300K。求：压缩每kg气体的总焰变。解：取压气机为控制体。按可逆定温压缩消耗轴功：100P=0.287×400lnWso = RT In 2 = RT In -264.3kJ/kgP21000V1实际消耗轴功：W, =1.25(-264.3)=-330.4kJ / kg由开口系统能量方程，忽略动能、位能变化：Ws+h=q+h因为理想气体定温过程：h=hz-45-

工程热力学例题与习题 —45— 由理想气体熵的计算式： k J k g k P P R T T S CP  = − = − = 0.069 /  0.1 0.42 0.287ln 293 473 ln ln 1.005ln 1 2 1 2 1 2 例 2：刚性容器中贮有空气 2kg，初态参数 P1=0.1MPa，T1=293K，内装搅 拌器，输入轴功率 WS=0.2kW，而通过容器壁向环境放热速率为 Q 0.1kW . = 。求： 工作 1 小时后孤立系统熵增。 解：取刚性容器中空气为系统，由闭系能量方程： W s = Q+ U . . 经 1 小时， ( ) 2 1 . . 3600W s = 3600Q+ mCv T −T ( ) K mC W Q T T v 544 2 0.7175 3600 0.2 0.1 293 3600 . . 2 1 =  − = +       − = + 由定容过程： 1 2 1 2 T T P P = ， MPa T T P P 0.186 293 544 0.1 1 2 2 = 1 =  = 取以上系统及相关外界构成孤立系统： Siso = Ssys + Ssur k J K T Q Ssur 1.2287 / 293 3600 0.1 0 =   = = Siso = 0.8906 +1.2287 = 2.12kJ / K 例 3：压气机空气由 P1=100kPa，T1=400K，定温压缩到终态 P2=1000kPa， 过程中实际消耗功比可逆定温压缩消耗轴功多 25%。设环境温度为 T0=300K。 求：压缩每 kg 气体的总熵变。 解：取压气机为控制体。按可逆定温压缩消耗轴功： k J k g P P RT v v WS O RT 264.3 / 1000 100 ln ln 0.287 400ln 2 1 1 2 = = =  = − 实际消耗轴功： WS =1.25(− 264.3) = −330.4kJ / kg 由开口系统能量方程，忽略动能、位能变化： WS + h1 = q + h2 因为理想气体定温过程：h1=h2

工程热力学例题与习题故：q=Ws=-330.4kJ/kg孤立系统焰增：ASio=ASsw+ASsm稳态稳流：AS=0是=Rn+号ASur =S, -S, +TPT100330.44=0.44kJ/kg-k=0.287ln1000300例4：已知状态P=0.2MPa，t=27℃的空气，向真空容器作绝热自由膨胀，终态压力为P=0.1MPa。求：作功能力损失。（设环境温度为T=300K）解：取整个容器（包括真空容器）为系统，由能量方程得知：U,=U,，T=T,=T对绝热过程，其环境变=C,n-Rn=0-RnASTAPP0.2 = 0.199kJ /kg.k= Rin β=0.287n %P0.1AW=TgASiso=300×0.44=132kJ/kg例5：如果室外温度为-10℃，为保持车间内最低温度为20℃，需要每小时向车间供热36000kJ，求：1）如采用电热器供暖，需要消耗电功率多少。2）如采用热泵供暖，供给热泵的功率至少是多少。3）如果采用热机带动热泵进行供暖，向热机的供热率至少为多少。图5.1为热机带动热泵联合工作的示意图。假设：向热机的供热温度为600K，热机在大气温度下放热。600KTo=270K293K9.100km>0.T=370K95kRw热机图5.2263K图5.1—46-

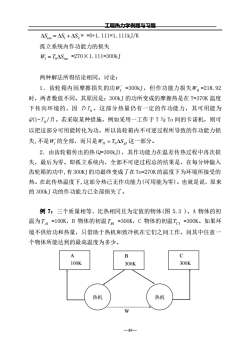
工程热力学例题与习题 —46— 故： q =WS = −330.4kJ / kg 孤立系统熵增： Siso = Ssys + Ssur 稳态稳流： Ssys = 0 k J k g k T q P P R T q Ssur S S = + =   = − + = + 0.44 / 300 330.4 1000 100 0.287 ln ln 2 0 1 0 2 1 例 4：已知状态 P1=0.2MPa，t1=27℃的空气，向真空容器作绝热自由膨胀， 终态压力为 P2=0.1MPa。求：作功能力损失。（设环境温度为 T0=300K） 解：取整个容器（包括真空容器）为系统， 由能量方程得知： U1 =U2，T1 = T2 = T 对绝热过程，其环境熵变 k J k g k P P R P P R P P R T T Ssys CP = = =   = − = − 0.199 / 0.1 0.2 ln 0.287ln ln ln 0 ln 2 1 1 2 1 2 1 2 W = T0Siso = 300  0.44 =132kJ / kg 例 5：如果室外温度为-10℃，为保持车间内最低温度为 20℃，需要每小 时向车间供热 36000kJ,求：1) 如采用电热器供暖,需要消耗电功率多少。2) 如采用热泵供暖，供给热泵的功率至少是多少。3) 如果采用热机带动热泵进 行供暖，向热机的供热率至少为多少。图 5.1 为热机带动热泵联合工作的示 意图。假设：向热机的供热温度为 600K，热机在大气温度下放热。 图 5.2 Q1  W  热泵 热机 图 5.1  Q1  600K 293K 263K

工程热力学例题与习题解：1用电热器供暖，所需的功率即等于供热率，故电功率为36000=10kwW=O:36002)如果热泵按逆向卡诺循环运行，而所需的功最少。则逆向卡诺循环的供暖系数为2-T:=9.77Gw=T, +T,W3=1.02kW热泵所需的最小功率为W=Cw3按题意，只有当热泵按逆卡诺循环运行时，所需功率为最小。只有当热机按卡诺循环运行时，输出功率为W时所需的供热率为最小。7, =1- =1- 2633=0.56由600T,1热机按所需的最小供热率为Om = W in -1.022=1.82kW0.56例6：一齿轮箱在温度T=370K的稳定状态下工作，输入端接受功率为100kW，而输出功率为95kW，周围环境为270K。现取齿轮箱及其环境为一孤立系统（见图5.2）1)试分析系统内发生哪些不可逆过程。并计算每分钟内各不可逆过程的焰产及作功能力的损失。计算系统的熵增及作功能力总的损失。解：1)此孤立系统内进行着两个不可逆过程：由于齿轮箱内部的摩擦将功变为热的过程，齿轮箱(T=370K)与环境(To=270K)间的温差传热过程。分别计算如下，每分钟内齿轮箱中损失的功W及传向环境的热QW=60X(100-95)=300kJ—47—

工程热力学例题与习题 —47— 解：1)用电热器供暖，所需的功率即等于供热率, 故电功率为 3600 36000 . . W = Q = = 10kW 2)如果热泵按逆向卡诺循环运行，而所需的功最少。则逆向卡诺循环的 供暖系数为 1 2 1 . . T T T W Q W +  = = =9.77 热泵所需的最小功率为 W Q W  . . = =1.02kW 3)按题意，只有当热泵按逆卡诺循环运行时，所需功率为最小。只有当 热机按卡诺循环运行时，输出功率为 . W 时所需的供热率为最小。 由 0.56 600 263 1 1 1 2 = − = − = T T c 热机按所需的最小供热率为 Q W tc 1.82kW 0.56 1.02 / . . min =  = = 例 6：一齿轮箱在温度 T=370K 的稳定状态下工作，输入端接受功率为 100kW，而输出功率为 95kW,周围环境为 270K。现取齿轮箱及其环境为一孤立 系统(见图 5.2) 1)试分析系统内发生哪些不可逆过程。并计算每分钟内各 不可逆过程的熵产及作功能力的损失。计算系统的熵增及作功能力总的损失。 解：1)此孤立系统内进行着两个不可逆过程：由于齿轮箱内部的摩擦将 功变为热的过程,齿轮箱(T=370K)与环境(To=270K)间的温差传热过程。分别 计算如下, 每分钟内齿轮箱中损失的功 ' Wl 及传向环境的热 Q ' Wl =60×(100-95)=300kJ

工程热力学例题与习题因齿轮箱在稳定状态下工作，人U=0其能量平衡关系为(-Q)=△U+W=0+60×95-60×100=-300kJ故Q=300kJ(2)齿轮箱内不可逆过程的熵产与作功能力损失摘产Wi=0.8108kJ /KAS=T作功能力损失Wn=ToAS.=270X0.8108=218.92kJ3）齿轮箱与环境间温差传热所引起的摘产与作功能力损失摘产1-11)=300(=0.3003kJ/K=O(1S2703701To作功能力损失Wiz2=TASg2=270×0.3003=81.08kJ2)孤立系统的熵增及作功能力的损失解一：孤立系统的摘增为各不可逆过程中产之和ASis.=△S.l+AS.2=0.8108+0.3003=1.111kJ/K作功能力总损失W=218.92+81.08=300kJ解二：孤立系统的熵增为齿轮箱的摘变化△S,与环境的熵变化△S。之和。因齿轮箱在稳定状态下工作，故其摘变化AS,=0而环境在温度T。=270K的情况下接受热量Q，故其熵变化为Q=1.11kJ/KAS,=9T。因此，孤立系统的摘增为48—

工程热力学例题与习题 —48— 因齿轮箱在稳定状态下工作， U = 0 其能量平衡关系为 (-Q)= U +W =0+60×95-60×100=-300kJ 故 Q=300kJ (2)齿轮箱内不可逆过程的熵产与作功能力损失 熵产 T W S l g '  1 = =0.8108kJ /K 作功能力损失 Wl1 = T0Sg1 = 270×0.8108=218.92kJ (3)齿轮箱与环境间温差传热所引起的熵产与作功能力损失 熵产 k J K T T Sg Q ) 0.3003 / 370 1 270 1 ) 300( 1 1 ( 0  2 = − = − = 作功能力损失 Wl 2 = T0Sg 2 = 270×0.3003=81.08kJ 2)孤立系统的熵增及作功能力的损失 解一： 孤立系统的熵增为各不可逆过程中熵产之和 Siso = Sg1 + Sg 2 =0.8108+0.3003=1.111kJ/K 作功能力总损失 W=218.92+81.08=300kJ 解二：孤立系统的熵增为齿轮箱的熵变化 1 S 与环境的熵变化 S g 之和。 因齿轮箱在稳定状态下工作，故其熵变化 1 S =0 而环境在温度 T 0 =270K 的情况下接受热量 Q，故其熵变化为 0 2 T Q S = = 1.11kJ/K 因此,孤立系统的熵增为

工程热力学例题与习题△Sis。 = △S, +△S, = =0+1. 111=1. 111kJ/K孤立系统内作功能力的损失W,=TASis。=270×1.111=300kJ两种解法所得结论相同。讨论：1.齿轮箱内因摩擦损失的功W，=300kJ，但作功能力损失W，=218.92时，两者数值不同。其原因是：300kJ的功所变成的摩擦热是在T=370K温度下传向环境的，因T>T。，这部分热量仍有一定的作功能力，其可用能为Q(1-T。/D)。若采取某种措施，例如采用一工作于T与To间的卡诺机，则可以把这部分可用能转化为功。所以齿轮箱内不可逆过程所导致的作功能力损失，不是W的全部，而只是W=TAS。这一部分。2.由齿轮箱传出的热（Q=300kJ)，其作功能力在温差传热过程中再次损失，最后为零。即孤立系统内，全部不可逆过程总的结果是，在每分钟输入齿轮箱的功中，有300KJ的功最终变成了在To=270K的温度下为环境所接受的热。在此传热温度下，这部分热已无作功能力（可用能为零）。也就是说，原来的300k功的作功能力已全部损失了。例7：三个质量相等、比热相同且为定值的物体（图5.3）。A物体的初温为T=100K，B物体的初温T=300K，C物体的初温Tc，=300K。如果环境不供给功和热量，只借助于热机和致冷机在它们之间工作，问其中任意一个物体所能达到的最高温度为多少。AcB300K100K300K热机热机W-49-

工程热力学例题与习题 —49— Siso = S1 + S2 = =0+1.111=1.111kJ/K 孤立系统内作功能力的损失 Wl = T0Siso =270×1.111=300kJ 两种解法所得结论相同。讨论： 1．齿轮箱内因摩擦损失的功 ' Wl =300kJ，但作功能力损失 Wl1 =218.92 时，两者数值不同。其原因是：300kJ 的功所变成的摩擦热是在 T=370K 温度 下传向环境的，因 T>T 0 ，这部分热量仍有一定的作功能力，其可用能为 Q(1-T 0 /T)。若采取某种措施，例如采用一工作于 T 与 To 间的卡诺机，则可 以把这部分可用能转化为功。所以齿轮箱内不可逆过程所导致的作功能力损 失,不是 ' Wl 的全部，而只是 Wl1 = T0Sg1 这一部分。 2．由齿轮箱传出的热(Q=300kJ)，其作功能力在温差传热过程中再次损 失，最后为零。即孤立系统内，全部不可逆过程总的结果是，在每分钟输入 齿轮箱的功中,有300KJ的功最终变成了在To=270K的温度下为环境所接受的 热。在此传热温度下,这部分热已无作功能力(可用能为零)。也就是说，原来 的 300kJ 功的作功能力已全部损失了。 例 7：三个质量相等、比热相同且为定值的物体(图 5.3 )。A 物体的初 温为 TA1 =100K，B 物体的初温 TB1 =300K，C 物体的初温 TC1 =300K。如果环 境不供给功和热量，只借助于热机和致冷机在它们之间工作，问其中任意一 个物体所能达到的最高温度为多少。 A 100K B 300K C 300K 热机 热机 W

工程热力学例题与习题图5.3解：因环境不供给功和热量，而热机工作必须要有两个热源才能使热量转变为功。所以三个物体中的两个作为热机的有限热源和有限冷源。致冷机工作必须要供给其机械功，才能将热量从低温热源转移到高温热源，同样有三个物体中的两个作为致冷机的有限冷源和有限热源。由此，其工作原理如图5.3所示。取A、B、C物体及热机和致冷机为孤立系。如果系统中进行的是可逆过程，则AS=ASE+ASE+AS,AS,+AS.=0对于热机和致冷机ASe=dS=0，则Te dTTe2dTTedTASiso=mc+mc=(+mcTTTTeiToInTa+n Tm2+h To2=0TA"TITciTz T2 Tc2 =1Ta TBi TciTa2TB2Tc2=TATBTc=100×300×300=9×10*K3(1)由图5.3可知，热机工作于A物体和B物体两有限热源之间，致冷机工作于B物体和C物体两有限热源及冷源之间，热机输出的功供给致冷机工作。当T42=TBz时，热机停止工作，致冷机因无功供给也停止工作，整个过程结束。过程进行的结果，物体B的热量转移到物体C使其温度升高，而A物体和B物体温度平衡。对该孤立系，由能量方程式得QA+QB+Qc=0mc(TA2- Ta)+mc(TB2 -TBl)+mc(Tc2 -Tcl)= 0TA2+TB2+Tc2=TA+TBi+Tcl=100+300+300=700K(2)根据该装置的工作原理可知，T2>Ta1,TB2Tc1,TA2=TB250—

工程热力学例题与习题 —50— 图 5.3 解：因环境不供给功和热量，而热机工作必须要有两个热源才能使热量 转变为功。所以三个物体中的两个作为热机的有限热源和有限冷源。致冷机 工作必须要供给其机械功，才能将热量从低温热源转移到高温热源，同样有 三个物体中的两个作为致冷机的有限冷源和有限热源。由此,其工作原理如图 5.3 所示。 取 A、B、C 物体及热机和致冷机为孤立系。如果系统中进行的是可逆 过程,则 Siso = SE + SE' + SA + SB + SC =0 对于热机和致冷机  S E = dS =0，则 0 2 1 2 1 2 1  = + + =    C C B B A A T T T T T T iso T dT mc T dT mc T dT S mc ln ln ln 0 1 2 1 2 1 2 + + = C C B B A A T T T T T T 1 1 2 1 2 1 2 = C C B B A A T T T T T T TA2TB2TC2 = TA1TB1TC1 =100×300×300=9× 8 3 10 K （1） 由图 5.3 可知，热机工作于 A 物体和 B 物体两有限热源之间，致冷机工 作于 B 物体和 C 物体两有限热源及冷源之间，热机输出的功供给致冷机工作。 当 TA2 =TB2 时，热机停止工作，致冷机因无功供给也停止工作，整个过程结 束。过程进行的结果，物体 B 的热量转移到物体 C 使其温度升高，而 A 物体 和 B 物体温度平衡。 对该孤立系，由能量方程式得 QA + QB + QC = 0 mc(TA2 −TA1 ) + mc(TB2 −TB1 ) + mc(TC2 −TC1 ) = 0 TA2 +TB2 +TC2 = TA1 +TB1 +TC1 =100 十 300+300=700K （2） 根据该装置的工作原理可知， 2 1 2 1 2 1 2 2 , , , TA  TA TB  TB TC  TC TA = TB

工程热力学例题与习题对式(1)与(2)求解,得TA2=TB2 =150KTc,=400K即可达到的最高温度为400K.讨论：若致冷机工作于A物体和C物体两有限冷源和热源之间，其过程结果又如何呢。请读者自行分析。例8：一刚性容器贮有700kg的空气，其初始压力p=1bar，t=5℃，若想要使其温度升高到t=27℃（设空气为理想气体，比热为定值）：（1）求实现上述状态变化需加入的能量？（2）如果状态的变化是从T=422K的热源吸热来完成，求整体的摘增？（3）如果状态的变化只是从一个功源吸收能量来完成，求整体的增？解（1）从热力学第一定律：净能量的输入=2一W2=Uh一U=m（u一u）=mc(T-T)x×8.314=700× 2(300-278)=11088kJ28.97(2)ASSsurtSsysT2+RnV2ASsvs=mc,n V, =V)T,ViT,= mc, In -T300(300—278)=700×0.72×0.076=38.385kJ/K=700X0.72ln2784Sm=0T。既然空气状态的变化是由于从T吸取的热量，而系统与环境又无功量交换所以62为净能量输入，只是对环境而言，6一2=一11088kI代入上式则得51-

工程热力学例题与习题 —51— 对式(1)与(2)求解,得 TA2 =TB2 =150K TC2 =400K 即可达到的最高温度为 400K. 讨论：若致冷机工作于 A 物体和 C 物体两有限冷源和热源之间，其过程 结果又如何呢。请读者自行分析。 例 8：一刚性容器贮有 700kg 的空气，其初始压力 p1=1bar，t1=5℃，若 想要使其温度升高到 t2=27℃（设空气为理想气体，比热为定值）： （1）求实现上述状态变化需加入的能量？ （2）如果状态的变化是从 T0=422K 的热源吸热来完成，求整体的熵增？ （3）如果状态的变化只是从一个功源吸收能量来完成，求整体的熵增？ 解 （1）从热力学第一定律： 净能量的输入=Q12－W12=U2－U1=m(u2－u1) =mcv(T2－T1) =700× 28.97 8.314 2 5  (300－278)=11088kJ （2） ΔS=ΔSsur+ΔSsys ΔSsvs= ln ln ( ) 2 1 1 2 1 2 v v v v R T T m cv  =      +  = 1 2 ln T T mcv =700×0.72 278 300 ln (300－278)=700×0.72×0.076=38.385kJ/K ΔSsur= T0 Q 既然空气状态的变化是由于从 T0吸取的热量，而系统与环境又无功量交换， 所以 Q12为净能量输入，只是对环境而言，Q=－Q12=－11088kJ 代入上式则得：

工程热力学例题与习题g-11088AS=26.275kJ/kT422:.△S-38.385—26.275=12.110kJ/K（3）因为没有热量加入：.△S=0△S=△Sss=38.385kJ/K例9：求出下述情况下，由于不可逆性引起的作功能力损失。已知大气p=1013215Pa，温度T为300K。TA=400K（1）将200kJ的热直接从p=po、温度为400KQ=200kJ的恒温热源传给大气。ToO=200kJ（2）200kJ的热直接从大气传向p=po、温度Q-200kJ为200K的恒温热源B。TB=200K（3）200kJ的热直接从热源A传给热源B。图5.4解：由题意画出示意图5.4。（1）将200kJ的热直接从400K恒温热源A传给300K的大气时，-200-9AS.-0.5kJ/KTA400Q200AS.=-0.667kJ/KT.300热源A与大气组成的系统熔变为AS, =AS,+AS=-0.5+0.667=0.167kJ/K此传热过程中不可逆性引起的作功能力损失为I =T.=300x0.167= 50.1kJ（2）200kJ的热直接从大气传向200K的恒温热源B时，9_200ASR=-=1kJ/KT20052-

工程热力学例题与习题 —52— ΔSsur= T Q = 422 11088 − =－26.275 kJ/k ∴ ΔS=38.385－26.275=12.110 kJ/K （3）因为没有热量加入 ∴ ΔSsur=0 ∴ ΔS=ΔSsys=38.385 kJ/K 例 9：求出下述情况下，由于不可逆性引起的作功能力损失。已知大气 p0=1013215Pa，温度 T0为 300K。 （1）将 200kJ 的热直接从 pA=p0、温度为 400K 的恒温热源传给大气。 （2）200kJ 的热直接从大气传向 pB=p0、温度 为 200K 的恒温热源 B。 （3）200kJ 的热直接从热源 A 传给热源 B。 解：由题意画出示意图 5.4。 （1）将 200kJ 的热直接从 400K 恒温热源 A 传给 300K 的大气时， 0.5 400 200 = − − = −  = A A T Q S kJ/K 0.667 300 200 0  0 = = = − T Q S kJ/K 热源 A 与大气组成的系统熵变为 0.167kJ/K 0.5 0.667 1 0 = = − + S = S A + S 此传热过程中不可逆性引起的作功能力损失为 50.1kJ 300 0.167 0 = =   = T （2）200kJ 的热直接从大气传向 200K 的恒温热源 B 时， 1 200 200  = = = B B T Q S kJ/K T0 Q=200kJ TA=400K TB=200K Q=200kJ Q=200kJ 图 5.4

工程热力学例题与习题4S, ==_-200=-0.667kJ/KT。300AS,=AS。+ASR=-0.667+1=0.333kJ/K此过程不可逆引起的作功能力损失II=TAS,=300×0.333=100kJ（3）200kJ直接从恒温热源A传给恒温热源B，则-200-0AS.=-0.5kJ/KTA400_200ASR==1kJ/K200T△S,=-0.5+1=0.5kJ/K作功能力损失II=T.4S,=300x0.5=150kJ可见（1）和（2）两过程的综合效果与（3）过程相同。5.5思考及练习题1.热力学第二定律是否可表达为：功可以完全变为热，但热不能完全变成功。为什么？2.自发过程为不可逆过程，那么非自发过程即为可逆过程。此说法对吗？为什么？3.自然界中一切过程都是不可逆过程，那么研究可逆过程又有什么意义呢?4．以下说法是否正确？①增大的过程必为不可逆过程②不可逆过程的焰变无法计算③若从某一初态沿可逆和不可逆过程达到同一终态，则不可逆过程中的焰变必定大于可递过程中的摘变。—53—

工程热力学例题与习题 —53— 0.667 300 200 0 0 = − − = −  = T Q S kJ/K 0.333kJ/K 2 0 0.667 1 = S = S + S B = − + 此过程不可逆引起的作功能力损失 100kJ 0 2 300 0.333 =  =  =   T S （3）200kJ 直接从恒温热源 A 传给恒温热源 B，则 0.5 400 200 = − − = −  = A A T Q S kJ/K 1 200 200  = = = B B T Q S kJ/K S3 = −0.5 +1 = 0.5 kJ/K 作功能力损失 300 0.5 150kJ  = T0S3 =  = 可见（1）和（2）两过程的综合效果与（3）过程相同。 5．5 思考及练习题 l．热力学第二定律是否可表达为：功可以完全变为热，但热不能完全变 成功。为什么? 2．自发过程为不可逆过程，那么非自发过程即为可逆过程。此说法对吗? 为什么? 3．自然界中一切过程都是不可逆过程，那么研究可逆过程又有什么意义 呢? 4．以下说法是否正确? ①熵增大的过程必为不可逆过程 ②不可逆过程的熵变无法计算 ③若从某一初态沿可逆和不可逆过程达到同一终态，则不可逆过程中的 熵变必定大于可逆过程中的熵变