《医学统计学》课程教学课件（PPT讲稿）常用概率分布

重废警科大学 Chongqing Medical University 常用概率分布 卫生统计学教研室 田考聪

常用概率分布 卫生统计学教研室 田考聪

重废警科大学 Chongqing Medical University 常用概率分布 二项分布 1.二项分布的概念 例换窘额缓个珠从中姿整男 解：由于是有只抽样，故每公摸到黄球的撼率均为QA,摸到归球的趣 率为0.。设摸到黄球的闪数为X,若次摸球中命X次摸到黄球，后书 次摸到白球，则相应的概率为： 0.40.65-x 由于摸到黄球可能发生在5次摸球的任意X次中，故5 次摸球中有X次摸到黄球的概率为： C0.40.65-x

常用概率分布 一、二项分布 1.二项分布的概念 例：一袋中装有2黄、3白共5个乒乓球。从中每次摸出1个，然后放回再 摸 先后摸5次，问摸到0、1、2、3、4、5次黄球的概率各有多大？ 解：由于是有放回抽样，故每次摸到黄球的概率均为0.4，摸到白球的概 率为0.6。设摸到黄球的次数为X，若5次摸球中前X次摸到黄球，后5- X次摸到白球，则相应的概率为： X 5−X 0.4 0.6 由于摸到黄球可能发生在5次摸球的任意X次中，故5 次摸球中有X次摸到黄球的概率为: X X X C 5− 5 0.4 0.6

重廣警科大学 Chongqing Medical University 本例的实验有以下三个特点： 每次摸球是彼此独立的： 。 每次摸球只有两种可能的结果； ·每次摸球出现某种结果的概率不变。 满足上述三个条件的随机试验称为Bernoullit试验。本例 摸了5次球，即进行了5次Bernoulli试验。 一般地，在n次Bernoulli试验中，事件A出现的概率为π 设为事件4出现的次数，则是一个离散型随机变量， 它服从二项分布，记为Bn,d,其概率函数为： P(x)=P(X=x)=Cπ*(1-π)”-xx=0,1,2,3,.,n n! C= 式(5-1) xl(n-x)！

本例的实验有以下三个特点： • 每次摸球是彼此独立的; • 每次摸球只有两种可能的结果; • 每次摸球出现某种结果的概率不变。 满足上述三个条件的随机试验称为Bernoulli试验。本例 摸了5次球，即进行了5次Bernoulli试验。 一般地，在n次Bernoulli试验中，事件A出现的概率为π ，设x为事件A出现的次数，则x是一个离散型随机变量， 它服从二项分布，记为B(n,π),其概率函数为： ( ) ( ) (1 ) 0,1,2,3, , ! !( )! x x n x n x n P x P X x C x n n C x n x   − = = = − = = − 式（5-1）

重废警科大学 Chongqing Medical University 在n次Bernoullit试验中， 事件A至多出现k次的概率为 2P)=2Cx1-π) x=0 事件A至少出现k次的概率为 ∑Px)=1-∑Cπ'1-) =0 例1：临床上用针灸治疗某型头痛，有效的概率为0.6， 现以该法治疗3例，其中2例有效的概率是多少？ 治疗结果为有效和无效两类，每个患者是否有效不 受其他病例的影响，有效概率均为0.6，符合二项分布条 件。本例π=0.6，=3，随机治疗3例，有效例数为2的概 率为： C0.62(1-0.6)3-2=0.432

在n次Bernoulli试验中， 事件A至多出现k次的概率为 事件A至少出现k次的概率为 0 0 ( ) (1 ) k k x x n x n x x P x C   − = =  = − 1 0 ( ) 1 (1 ) n k x x n x n x k x P x C   − − = =   = − − 例1：临床上用针灸治疗某型头痛，有效的概率为0.6， 现以该法治疗3例，其中2例有效的概率是多少？ 治疗结果为有效和无效两类，每个患者是否有效不 受其他病例的影响，有效概率均为0.6，符合二项分布条 件。本例π= 0.6，n =3,随机治疗3例，有效例数为2的概 率为： 0.6 (1 0.6) 0.432 2 2 3 2 3 − = − C

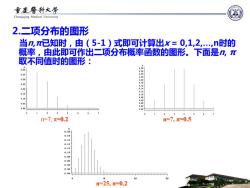
重废警科大学 Chongqing Medical University 2.二项分布的图形 当n,己知时，由（5-1)式即可计算出x=0,1,2,n时的 概率，由此即可作出二项分布概率函数的图形。下面是n,π 取不同值时的图形： 、 0.30 0.25 .s 0,5 0,0 n=7,=0.2 =7,=0.5 0.18 8 0:10 0.08 0.06 0.04 0.00 10 20 30 n=25,π=0.2

2.二项分布的图形 当n,π已知时，由（5-1）式即可计算出x = 0,1,2,.,n时的 概率，由此即可作出二项分布概率函数的图形。下面是n, π 取不同值时的图形： n=7, π=0.2 n=7, π=0.5 n=25, π=0.2

重废警科大学 Chongqing Medical University 3.二项分布的性质 1)对于固定的和π， 当x(n+1)π时，Px)随着的增大而减小， 当x=[(n+1)d时，Px达到最大值。 2)当π=1-π=0.5时，二项分布呈对称分布， 当π≠1-时，二项分布呈偏态分布 当n增大时，二项分布逐渐近似于对称分布。 3)二项分布的数字特征： 总体均数：W=nπ 总体方差：G=nπ（1-π） 总体标准差：o=√nπ(l-π)

3.二项分布的性质 1)对于固定的n和π， 当 x (n+1)π时， P(x)随着x的增大而减小， 当 x = [(n+1)π]时，P(x)达到最大值。 2)当π=1-π=0.5时，二项分布呈对称分布， 当π≠1-π时，二项分布呈偏态分布， 当 n 增大时，二项分布逐渐近似于对称分布。 3)二项分布的数字特征： 总体均数：μ= nπ 总体方差：σ2 = nπ（1-π） 总体标准差：    = − n (1 )

重废警科大学 Chongqing Medical University 将出现阳性结果的频率记为：P=Xn, 则 的总体均数：4。=π p的总体方差：o=π-型 n 的总体标准差（又称为率的标准误）： π(1-π) 0n三 n 例2：已知某地钩虫感染率为6.7%，如果随机抽查该地 150人，记X为感染人数，p=Xn为样本感染率，则： X的总体均数u=nπ=150×0.067=10.05 p的总体均数4，=π=0.067

若将出现阳性结果的频率记为：p= X/n， 则 p的总体均数： p的总体方差： p的总体标准差(又称为率的标准误)： 2 (1 ) p n    − =   p = (1 ) p n    − = 例2：已知某地钩虫感染率为6.7%，如果随机抽查该地 150人，记X为感染人数，p = X/n为样本感染率，则： X的总体均数  = n =1500.067 =10.05 p的总体均数  p =  = 0.067

重废警科大学 Chongqing Medical University X的总体标准差 0=Vnπ(1-π)=V150×0.0671-0.067）=3.062 p的总体标准差（即频率的标准误） π(1-π) 0.067(1-0.067) =0.020 150

X 的总体标准差 p 的总体标准差 (即频率的标准误)  = n(1−) = 1500.067(1−0.067) = 3.062 0.020 150 (1 ) 0.067(1 0.067) = − = − = n p   

重废警科大学 Chongqing Medical University 4.二项分布的应用 例3：如果某地钩虫感染率为13%，随机观察当地150人， 其中有10人感染钩虫的概率有多大？至多有2人感染 钩虫的概率有多大？至少有2人感染钩虫的概率有多 大？至少有20人感染钩虫的概率有多大？ 因为人与人之间钩虫感染与否是相互独立的，可 以认为感染钩虫的人数服从150，π0.13的二项 分布，于是有：

4.二项分布的应用 例3:如果某地钩虫感染率为13%，随机观察当地150人， 其中有10人感染钩虫的概率有多大？至多有2人感染 钩虫的概率有多大？至少有2人感染钩虫的概率有多 大？至少有20人感染钩虫的概率有多大？ 因为人与人之间钩虫感染与否是相互独立的，可 以认为感染钩虫的人数X服从n=150, π=0.13的二项 分布，于是有：

重废警科大学 Chongqing Medical University 有10人感染的概率为： P(Y=10)=C19o0.1310.87150-10 1501 0.13100.8750-10=0.0055 101(150-10)1 至多有2人感染的概率为： P(X≤2)=∑C50.13*0.87150X X=0 =8.47×10-10+1.90×10-8+2.11×10-7=2.31×10-2

0.13 0.87 0.0055 10!(150 10)! 150! ( 10) 0.13 0.87 1 0 150 1 0 1 0 1 0 150 1 0 150 = − = = = − − P X C 1 0 8 7 2 2 0 150 150 8.47 10 1.90 10 2.11 10 2.31 10 ( 2) 0.13 0.87 − − − − = − =  +  +  =   =  X X X X P X C 有10人感染的概率为： 至多有2人感染的概率为：