《医学统计学》课程教学课件（PPT讲稿）方差分析 Analysis of Variance, ANOVA

重唐隳科大学 Chongqing Medical University 方差分析 Analysis of Variance,ANOVA 卫生统计学教研室彭斌

方差分析 Analysis of Variance, ANOVA 卫生统计学教研室 彭斌

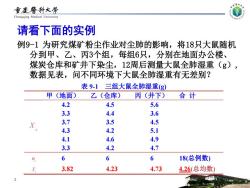
重废警科大学 Chongqing Medical University 请看下面的实例 例9-1为研究煤矿粉尘作业对尘肺的影响，将18只大鼠随机 分到甲、乙、丙3个组，每组6只，分别在地面办公楼、 煤炭仓库和矿井下染尘，12周后测量大鼠全肺湿重（g)， 数据见表，问不同环境下大鼠全肺湿重有无差别？ 表9-1三组大鼠全肺湿重(g) 甲（地面） 乙（仓库） 丙（井下) 合计 4.2 4.5 5.6 3.3 4.4 3.6 X 3.7 3.5 4.5 4.3 4.2 5.1 4.1 4.6 4.9 3.3 4.2 4.7 n 6 6 6 18(总例数) 3.82 4.23 4.73 4.26(总均数)

请看下面的实例 例9-1 为研究煤矿粉尘作业对尘肺的影响，将18只大鼠随机 分到甲、乙、丙3个组，每组6只，分别在地面办公楼、 煤炭仓库和矿井下染尘，12周后测量大鼠全肺湿重（g）, 数据见表，问不同环境下大鼠全肺湿重有无差别？ 2 表 9-1 三组大鼠全肺湿重(g) 甲（地面） 乙（仓库） 丙（井下） 合 计 i j X 4.2 4.5 5.6 3.3 4.4 3.6 3.7 3.5 4.5 4.3 4.2 5.1 4.1 4.6 4.9 3.3 4.2 4.7 i n 6 6 6 18(总例数) Xi 3.82 4.23 4.73 4.26(总均数)

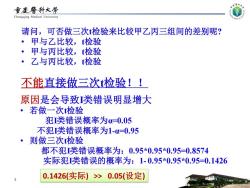
重废警科大学 Chongqing Medical University 请问，可否做三次t检验来比较甲乙丙三组间的差别呢？ ·甲与乙比较，检验 ·甲与丙比较，检验 ·乙与丙比较，检验 不能直接做三次检验！！ 原因是会导致类错误明显增大 ·若做一次检验 犯类错误概率为=0.05 不犯类错误概率为1-u=0.95 ·则做三次检验 都不犯类错误概率为：0.95*0.95*0.95=0.8574 实际犯类错误的概率为：1-0.95*0.95*0.95=0.1426 0.1426(实际)>0.05（设定）

请问，可否做三次t检验来比较甲乙丙三组间的差别呢? • 甲与乙比较，t检验 • 甲与丙比较，t检验 • 乙与丙比较，t检验 3 原因是会导致I类错误明显增大 • 若做一次t检验 犯I类错误概率为α=0.05 不犯I类错误概率为1-α=0.95 • 则做三次t检验 都不犯I类错误概率为：0.95*0.95*0.95=0.8574 实际犯I类错误的概率为：1- 0.95*0.95*0.95=0.1426 不能直接做三次t检验！！ 0.1426(实际) >> 0.05(设定)

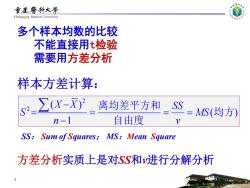
重废警科大学 Chongqing Medical University 多个样本均数的比较 不能直接用t检验 需要用方差分析 样本方差计算： S2ΣX-万)2 离均差平方和SS MS(均方) n-l 自由度 SS:Sum of Squares;MS:Mean Square 方差分析实质上是对SS和进行分解分析

样本方差计算： 4 多个样本均数的比较 不能直接用t检验 需要用方差分析 ( ) 1 ( ) 2 2 均方 自由度 离均差平方和 MS v SS n X X S = = = − − =  SS： Sum of Squares； MS：Mean Square 方差分析实质上是对SS和v进行分解分析

重废警科大学 Chongqing Medical University 主要内容 方差分析的基本思想 ·完全随机设计资料的方差分析 ·随机区组设计资料的方差分析 ·样本均数间的多重比较 ,方差分应用条件与数据变换（了解）

主要内容 • 方差分析的基本思想 • 完全随机设计资料的方差分析 • 随机区组设计资料的方差分析 • 样本均数间的多重比较 • 方差分析应用条件与数据变换（了解） 5

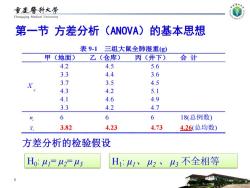
重废警科大学 Chongqing Medical University 第一节方差分析（ANOVA)! 的基本思想 表9-1三组大鼠全肺湿重(g) 甲（地面） 乙（仓库） 丙（井下） 合计 4.2 4.5 5.6 3.3 4.4 3.6 X 3.7 3.5 4.5 4.3 4.2 5.1 4.1 4.6 4.9 3.3 4.2 4.7 n 6 6 6 18(总例数) 3.82 4.23 4.73 4.26(总均数) 方差分析的检验假设 H0:4F23 H1:、42、43不全相等

表 9-1 三组大鼠全肺湿重(g) 甲（地面） 乙（仓库） 丙（井下） 合 计 4.2 4.5 5.6 3.3 4.4 3.6 3.7 3.5 4.5 4.3 4.2 5.1 4.1 4.6 4.9 i j X 3.3 4.2 4.7 i n 6 6 6 18(总例数) Xi 3.82 4.23 4.73 4.26(总均数) 6 H0 : μ1= μ2= μ3 H1 : μ1、 μ2 、 μ3 不全相等 方差分析的检验假设 第一节 方差分析（ANOVA）的基本思想

重废警科大学 Chongqing Medical University 表9-1 三组大鼠全肺湿重(g) 甲（地面) 乙（仓库） 丙（井下） 合计 4.2 4.5 5.6 3.3 4.4 3.6 3.7 3.5 4.5 4.3 4.2 5.1 4.1 4:6 4.9 3.3 4.2 4.7 6 6 6 18(总例数) 3.82 4.23 4.73 4.26(总均数) 从这个表，可以观察到三种变异： 1、全部数据间的变异，总变异 2、三组均数之间的变异，组间变异 3、每组内部数据间的变异，组内变异

表 9-1 三组大鼠全肺湿重(g) 甲（地面） 乙（仓库） 丙（井下） 合 计 i j X 4.2 4.5 5.6 3.3 4.4 3.6 3.7 3.5 4.5 4.3 4.2 5.1 4.1 4.6 4.9 3.3 4.2 4.7 i n 6 6 6 18(总例数) Xi 3.82 4.23 4.73 4.26(总均数) 7 从这个表，可以观察到三种变异： 1、全部数据间的变异，总变异 2、三组均数之间的变异，组间变异 3、每组内部数据间的变异，组内变异

重廣警科大学 Chongqing Medical University 变异（离均差平方和）的分解 1、 总变异（SS总，total variation） 全部测量值大小各异，与总均值之间的 差异称为总变异，即X,与灭之间的差异。 SSa=∑∑(X,-X)1 i=1j=1 本例，SS总=6.5628 8

变异(离均差平方和)的分解 1、总变异（SS总,total variation） 全部测量值大小各异，与总均值之间的 差异称为总变异，即Xij 与 之间的差异。 = = = − k i n j i j i SS X X 1 1 2 总 ( ) X 8 本例，SS总=6.5628

重废警科大学 Chongqing Medical University 2、组间变异 2(SS组间，variation between groups） ·三种环境下全肺湿重的平均值各不相同，这种 变异称为组间变异 ” 是组内均值X,与总均值X之差的平方和 SS同=∑∑(X,-X)2=∑n(仅，-) i=l 组间变异SS组▣反映： >三种不同环境对全肺湿重的影响（处理的效应） >同时也包括随机因素的影响（随机误差） 本例，SS组间=2.5278

2、组间变异（SS组间，variation between groups） • 三种环境下全肺湿重的平均值各不相同，这种 变异称为组间变异 • 是组内均值 与总均值 之差的平方和 2 1 1 2 SS (X X ) n (X X ) i k i i k i n j i i =  − =  − = = 组间 组间变异SS组间反映： ➢三种不同环境对全肺湿重的影响（处理的效应） ➢同时也包括随机因素的影响（随机误差） Xi X 9 本例，SS组间=2.5278

重废警科大学 Chongqing Medical University 3、组内变异(SS组内，variation within groups) ·在相同环境下生活，全肺湿生也各不相同，这种变 异称为组内变异 ·组内各个观测值X,与本组内均值x,之间差的平方和 SS内=∑∑(X,-X,)月 i=l i 组内变异SS组内反映： 本例， >随机因素的影响（随机误差） SS组内=4.0350 故，组内变异也常记为SS误差 10

3、组内变异(SS组内，variation within groups) • 在相同环境下生活，全肺湿生也各不相同，这种变 异称为组内变异 • 组内各个观测值 与本组内均值 之间差的平方和 2 1 1 ( ) i k i n j SS Xi j X i =  − = = 组内 Xij Xi 10 组内变异SS组内反映： ➢随机因素的影响（随机误差） 故，组内变异也常记为SS误差 本例， SS组内=4.0350