北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§3.1 二维随机向量及其分布函数 §3.2 二维离散型随机向量 §3.3 二维连续型随机向量

第三章随机向量 有些随机现象只用一个随机变量来描述是 不够的,需要用几个随机变量来同时描述。 例如: 1.某人体检数据 血压X和心律Y; 2.钢的基本指标 含碳量X,含硫量和 硬度Z; 3.导弹在空中位置一 坐标X,Y,Z
第三章 随机向量 有些随机现象只用一个随机变量来描述是 不够的,需要用几个随机变量来同时描述。 3. 导弹在空中位置——坐标(X, Y, Z)。 1. 某人体检数据——血压X和心律Y; 例如: 2. 钢的基本指标——含碳量X,含硫量 Y和 硬度 Z ;

般地,将随机试验涉及到的个随机 量X,X,X放在一起,记成(X,X, X),称n维随机向量(或变量)。 由于从二维随机向量推广到多维随机向 量并无实质性困难,所以,我们着重讨论二 维随机向量
一般地, 将随机试验涉及到的 n 个随机 量 X1, X2 , ., Xn 放在一起,记成(X1, X2 , ., Xn ),称 n 维随机向量(或变量)。 由于从二维随机向量推广到多维随机向 量并无实质性困难,所以,我们着重讨论二 维随机向量

§3.1二维随机向量及其分布函数 设试验E的样本空间为2,X=X(O)与Y= Y(o)是定义在2上的两个随机变量,由它们构 成的向量(X,)称为二维随机向量。 二维随机向量X,)的性质不仅与X和Y 的性质有关,而且还依赖于和Y之间的相互 关系。因此,必须把X,)作为一个整体来看 待,加以研究。 为此,首先引入二维随机向量X,)的分 布函数的概念
§3.1 二维随机向量及其分布函数 设试验E的样本空间为Ω,X=X()与Y= Y()是定义在Ω上的两个随机变量, 由它们构 成的向量 (X, Y) 称为二维随机向量。 二维随机向量(X, Y)的性质不仅与X 和Y 的性质有关,而且还依赖于X和Y之间的相互 关系。因此,必须把(X, Y)作为一个整体来看 待,加以研究。 为此,首先引入二维随机向量(X, Y)的分 布函数的概念

定义二维随机向量X,)的联合分布函数为 F(x,y)=P(X≤x,Y≤y), 一o0<X≤0 一0≤y<0. 如果将X,Y)看成平面上随机点的坐标。 取定xo,yo∈R=(-o,o),F(xo,Jyo)就是点(X,Y) 落在平面上,以(xoy)为顶点,且位于该点 左下方无限矩形区域上的概率
定义二维随机向量(X, Y) 的联合分布函数为 , . ( , ) ( , ), − − = x y F x y P X x Y y 取定x0,y0R=(-∞,∞), F(x0,y0)就是点(X,Y) 落在平面上,以(x0,y0)为顶点,且位于该点 左下方无限矩形区域上的概率。 如果将 (X, Y) 看成平面上随机点的坐标

(0%) @@的
说明 由上面的几何解释, 易见:随机点(X,Y)落在矩 形区域: x1x≤x2,y1y≤y2 内的概率为 P{x1<X≤2,Jy12} =Fc2,y2)广Fc2,y1)厂Fc1,Jy2+Fc1,Jy1) @@网
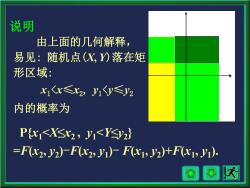
由上面的几何解释, 易见: 随机点(X, Y)落在矩 形区域: x1<x≤x2, y1<y≤y2 内的概率为 P{x1<X≤x2 , y1<Y≤y2 } =F(x2 , y2 )-F(x2 , y1 )- F(x1 , y2 )+F(x1 , y1 ). 说明

二维分布函数Fx,y)的三条基本性质 (1).F化,y)是变量x,y的非减函数; 即yeR给定,当x1<x2时, F(1,y)<F(x2,y). 同样,VxeR给定,当y2时, F(x,y )<F(x,y2). (2).x,y∈R,有0≤Fx,y)≤1; @四的
二维分布函数 F(x, y)的三条基本性质 (1).F(x, y)是变量 x,y 的非减函数; 即 yR给定,当 x1< x2 时, F(x1 , y)≤F(x2 , y). 同样, xR 给定,当y1≤y2时, F(x, y1 )≤F(x, y2 ). (2).x, yR, 有 0≤F(x, y)≤1;

(3).Vy∈R,F(-0,y)=0, Vx∈R,Fx,-oo=0, F(-00,-0o=0,F(0,o)=1. 其中 F(-o,y)=lim F(x,y), ●0 F(x,-oo)=lim F(x,y), F(-o,-∞)=,liF(x,y), Y,V->-c0 F(o,o)=m.Fx,)
(3). yR, F(-∞, y)=0, xR, F(x, -∞)=0, F(-∞, -∞)=0,F(∞, ∞)=1. ( , ) lim ( , ). ( , ) lim ( , ) , ( , ) lim ( , ), ( , ) lim ( , ) , , , F F x y F F x y F x F x y F y F x y x y x y y x → →− →− →− = − − = − = − = 其中

§3.2三维离散型随机向量 如果随机向量X,)的每个分量都是离 散型随机变量,则称X,)是二维离散型随 机向量。 二维离散型随机向量X,)所有可能取 的值也是有限个,或可列无穷个
§3.2 二维离散型随机向量 如果随机向量 (X, Y) 的每个分量都是离 散型随机变量,则称 (X, Y) 是二维离散型随 机向量。 二维离散型随机向量(X, Y) 所有可能取 的值也是有限个,或可列无穷个

离散型随机变量 离散型随机向量 X的概率分布: X,)的联合概 率分布: P(X=xk)=Pk> P(X=x,Y=yjPu k=1,2, i,j=1,2, Pk≥0,k=1,2, p,≥0,1,j=1,2,. ∑Σp,=1
离散型随机变量 X 的概率分布: = = = 1,2, ( ) , kP X x k p k = = k k k p p k 1. 0, 1,2, 离散型随机向量 (X, Y) 的联合概 率分布: , 1 , 2 , . ( , ) , = = = = i j P X x i Y y j pi j = = i j i j i j p p i j 1. 0, , 1,2,
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§2.4 随机变量函数的分布.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§2.3 连续型随机变量.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§2.2 离散型随机变量.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§1.5 事件的独立性 §2.1 随机变量.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§1.4 条件概率.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§1.2 事件的概率 §1.3 古典概率模型.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§1.1 基本概念(主讲教师:程维虎).ppt
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)概率习题补充30题.doc
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)07 参数估计.pdf
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)06 样本及抽样分布.pdf
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)05 极限定理.pdf
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)04 数字特征.pdf
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)03 多维随机变量及其分布.pdf
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)02 随机变量及其分布.pdf
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)01 概率论的基本概念.pdf
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)综合习题6.ppt
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)综合习题5.ppt
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)综合习题4.ppt
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)综合习题3.ppt
- 新疆大学:《概率与数理统计》课程教学资源(作业习题解)综合习题2.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§3.4 边缘分布 §3.5 条件分布.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§3.6 随机变量的独立性 §3.7 随机变量函数的分布.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)第四章 数字特征 §4.1 数学期望.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§4.2 方差.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§4.3 协方差与相关系数 §4.3 矩与协方差矩阵.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§5.1 大数定律 §5.2 中心极限定理.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)第六章 样本与统计量 §6.1 引言 §6.2 总体与样本 §6.3 统计量.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§6.4 正态总体.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)第七章 参数估计 §7.1 矩估计 §7.2 极大似然估计.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§7.3 估计量的优良性准则 §7.4 正态总体的区间估计(一).ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§7.5 正态总体的区间估计(二)§7.6 非正态总体的区间估计.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)第八章 假设检验 §8.1 基本概念 §8.2 正态总体均值的假设检验.ppt
- 北京工业大学:《概率与数理统计》课程教学资源(PPT课件讲稿)§8.3 正态总体方差的检验 §8.4 拟合优度检验.ppt
- 新疆大学:《概率与数理统计》课程授课教案(PPT教学课件)第一章 概率论的基本概念 第1节 随机事件的概率.ppt
- 新疆大学:《概率与数理统计》课程授课教案(PPT教学课件)第一章 概率论的基本概念 第2节 等可能概型与几何概型.ppt
- 新疆大学:《概率与数理统计》课程授课教案(PPT教学课件)第一章 概率论的基本概念 第3节 条件概率.ppt
- 新疆大学:《概率与数理统计》课程授课教案(PPT教学课件)第一章 概率论的基本概念 第4节 独立性.ppt
- 新疆大学:《概率与数理统计》课程授课教案(PPT教学课件)第一章 概率论的基本概念 第5节 n重贝努里概型.ppt
- 新疆大学:《概率与数理统计》课程授课教案(PPT教学课件)第二章 随机变量及其分布 第1节 随机变量.ppt
- 新疆大学:《概率与数理统计》课程授课教案(PPT教学课件)第二章 随机变量及其分布 第2节 离散型随机变量.ppt
