《食品工程原理》课程授课教案（B）第一章 流体力学

第2，3，4，5次课，8学时：教学目的和教学要求：流体力学的基本概念，流体的粘性与黏度，稳定流动体系的总能量方程，连续性方程，管内流动的阻力和流速分布，管路计算，流量测量，泵的类型与性能，泵的工作点与安装高度。重点和难点：重点掌握牛顿定律，连续性方程以及柏努力方程及其应用。第1章 流体力学基础流体包括气体和液体两种，其主要特征是可以流动。1基础知识与概念1．1物理量的单位(1)基本单位和导出单位任何物理量的大小都是由数字和单位联合来表达的，一般先选择几个独立的物理量，根据使用方便的原则规定出它们的单位，这些选择的物理量称为基本物理量，其单位称为基本单位。其他

第 2，3，4，5 次课，8 学时： 教学目的和教学要求： 流体力学的基本概念，流体的粘性与黏度，稳定流动体 系的总能量方程，连续性方程，管内流动的阻力和流速分布， 管路计算，流量测量，泵的类型与性能，泵的工作点与安装 高度。 重点和难点： 重点掌握牛顿定律，连续性方程以及柏努力方程及其应 用。 第 1 章 流体力学基础 流体包括气体和液体两种，其主要特征 是可以流动。 1 基础知识与概念 1．1 物理量的单位 (1)基本单位和导出单位 任何物理量的大 小都是由数字和单位联合来表达的，一般先 选择几个独立的物理量，根据使用方便的原 则规定出它们的单位，这些选择的物理量称 为基本物理量，其单位称为基本单位。其他

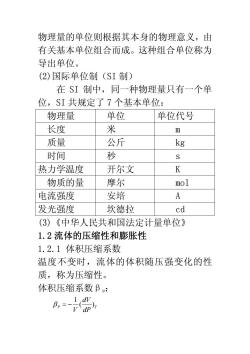
物理量的单位则根据其本身的物理意义，由有关基本单位组合而成。这种组合单位称为导出单位。(2)国际单位制（SI制）在SI制中，同一种物理量只有一个单位，SI共规定了7个基本单位：单位物理量单位代号长度米m公斤质量kg秒时间sK热力学温度开尔文摩尔mol物质的量A电流强度安培发光强度坎德拉cd(3）《中华人民共和国法定计量单位》1.2 流体的压缩性和膨胀性1.2.1体积压缩系数温度不变时，流体的体积随压强变化的性质，称为压缩性。体积压缩系数βp：1(dvβp=V(ap)

物理量的单位则根据其本身的物理意义，由 有关基本单位组合而成。这种组合单位称为 导出单位。 (2)国际单位制（SI 制） 在 SI 制中，同一种物理量只有一个单 位，SI 共规定了 7 个基本单位： 物理量 单位 单位代号 长度 米 m 质量 公斤 kg 时间 秒 s 热力学温度 开尔文 K 物质的量 摩尔 mol 电流强度 安培 A 发光强度 坎德拉 cd (3)《中华人民共和国法定计量单位》 1.2 流体的压缩性和膨胀性 1.2.1 体积压缩系数 温度不变时，流体的体积随压强变化的性 质，称为压缩性。 体积压缩系数βp： P T dP dV V )( 1 β −=

对于理想气体，状态方程为： PV=nRT体积压缩系数β,为：β,=1/Pβ与P成反比，即高压下难于压缩；低压下易于压缩。1.2.2体积膨胀系数压强不变时，流体的体积随温度变化的性质，称为膨胀性。体积膨胀系数βr：1 ,dVBr=()对于理想气体，有：βr=1/Tβ与T成反比，即高温下难于膨胀；低温下易于膨胀。1.2.3不可压缩流体的概念定义 ββ=βr=O 的流体为不可压缩流体。实际上，不可压缩的流体是不存在的。但在通常情况下，液体以及低速运动的气体可看作不可压缩流体。1.2.4流体压强的表示方法

对于理想气体，状态方程为： PV=nRT 体积压缩系数βp为： βp=1/P βP与P成反比，即高压下难于压缩；低压 下易于压缩。 1.2.2 体积膨胀系数 压强不变时，流体的体积随温度变化的性 质，称为膨胀性。 体积膨胀系数βT： T P dT dV V )( 1 β = 对于理想气体，有： βT=1/T βT与T成反比，即高温下难于膨胀；低温下 易于膨胀。 1.2.3 不可压缩流体的概念 定义βP=βT=0 的流体为不可压缩流体。 实际上，不可压缩的流体是不存在的。但在 通常情况下，液体以及低速运动的气体可看 作不可压缩流体。 1.2.4 流体压强的表示方法

流体的压强有绝对压强和表压强(或真空度)两种表示方法。以绝对零压为基准计算的压强，称为绝对压强;以大气压为基准计算的压强，称为表压强(或真空度）。该值是用仪表测出来的，当所测处的压强为大气压时，其读数为零。-般把绝对压强高于大气压的数值称为表压强，把绝对压强低于大气压的数值称为真空度。基本关系是：表压强=绝对压强-大气压强真空度=大气压强-绝对压强二-(绝对压强-大气压强)：表压强=-真空度表压强绝对压强压大气压强强真空度绝对压强绝对零压

流体的压强有绝对压强和表压强(或真空度) 两种表示方法。 以绝对零压为基准计算的压强，称为绝对压 强； 以大气压为基准计算的压强，称为表压强 (或真空度)。该值是用仪表测出来的，当所 测处的压强为大气压时，其读数为零。 一般把绝对压强高于大气压的数值称 为表压强，把绝对压强低于大气压的数值称 为真空度。 基本关系是： 表压强=绝对压强-大气压强 真空度=大气压强-绝对压强 =-(绝对压强-大气压强) ∴ 表压强=-真空度 表压强 绝对压强 压 大气压强 强 真空度 绝对压强 绝对零压

压强的单位：SI中为Pa;压强的几个单位间的换算关系：1atm=760mmHg=10. 33mH20=1. 01325X10'Pa1kgf/cm2=1at=735. 6mmHg=10mH0=9. 81 X 10'Pa2流体流动现象与流动阻力2．1牛顿内摩擦（粘性）定律与粘度粘性：流体质点间相对运动时产生阻力的性质。产生的原因：1）分子间的引力；2）分子的横向掺混→动量交换。结果：流动有阻力，需耗能量。粘性的大小用粘度来度量。牛顿对许多流体进行实验，发现如下规律：作用在流体上的剪应力与速度梯度成正比，即：F-tududyT=A-崇:流速在与流动方向相垂直的坐标方向上dy的变化率，称为速度梯度

压强的单位：SI 中为 Pa； 压强的几个单位间的换算关系： 1atm=760mmHg=10.33mH2O =1.01325×105 Pa 1kgf/cm2 =1at=735.6mmHg=10mH2O =9.81×104 Pa 2 流体流动现象与流动阻力 2．1 牛顿内摩擦（粘性）定律与粘度 粘性：流体质点间相对运动时产生阻力的性 质。 产生的原因：1）分子间的引力；2）分子的 横向掺混→动量交换。 结果：流动有阻力，需耗能量。 粘性的大小用粘度来度量。 牛顿对许多流体进行实验，发现如下规律： 作用在流体上的剪应力与速度梯度成正比， 即： dy du A F ±== μτ : dy du 流速在与流动方向相垂直的坐标方向上 的变化率，称为速度梯度

上式称为牛顿粘性定律，比例系数即为粘度。粘度的单位：在SI中为Pa.S;在其它单位制中，用P（泊）和cP（厘泊）。换算关系：1Pa.s=10P=1000cP运动粘度：流体的粘度与密度的比值，即U=u/p运动粘度的单位：在SI中为m2/s；在其它单位制中，用St（cm/s，斯)和cSt（厘斯)。换算关系：1m2/s=104St=10°cSt通常，流体的粘度与压强无关，仅与温度有关:Tt,μ,μct。2.2牛顿流体与理想流体牛顿流体：服从牛顿粘性定律的流体。理想流体：流体的粘度μ=0的流体。2.3流量与流速流速u：单位时间内流体在流动方向上所流过的距离，m/s。工程上指在管道截面上的平均流速。质量流速G：单位时间、单位管道截面所流

上式称为牛顿粘性定律，比例系数即为粘 度。 粘度的单位：在 SI 中为 Pa.s； 在其它单位制中，用 P（泊）和 cP（厘泊）。 换算关系： 1Pa.s=10P=1000cP 运动粘度υ：流体的粘度与密度的比值，即 υ = μ / ρ 运动粘度的单位：在SI中为m2 /s； 在其它单位制中，用St(cm2 /s，斯)和cSt（厘 斯）。 换算关系： 1m2 /s =104 St=106 cSt 通常，流体的粘度与压强无关，仅与温度有 关： T↑，μL↓，μG↑。 2.2 牛顿流体与理想流体 牛顿流体:服从牛顿粘性定律的流体。 理想流体:流体的粘度μ=0 的流体。 2．3 流量与流速 流速 u：单位时间内流体在流动方向上所流 过的距离，m/s。工程上指在管道截面上的 平均流速。 质量流速G：单位时间、单位管道截面所流

过的流体质量，kg/m2.s。流量：单位时间内流过管道任一截面的流体量，有体积流量Q（Vs）（m/s）和质量流量ws (kg/s)。以上几个物理量的关系：Q= uA体积流量g_或u=A管道截面积W, =GA质量流量或 G=_A管道截面积w, =GA = pQ= puAG= pu钢管的表示法：Φd.×（mm）d-管子外径，mm；8-壁厚，mm。管内径d;=do-2 8 mm例子：某钢管为Φ108X4mm，求内径。管内径d;=do-2 8 =108-2×4=100mm=0.1m2．4　流动类型与雷诺准数雷诺实验装置如图所示：

过的流体质量，kg/m2 .s。 流量：单位时间内流过管道任一截面的流体 量，有体积流量Q（Vs）（m3 /s）和质量流量 ws（kg/s）。 以上几个物理量的关系： = uAQ 或 管道截面积 体积流量 == A Q u s = GAw 或 管道截面积 质量流量 == A w G s s == ρ = ρuAQGAw = ρuG 钢管的表示法： Φd0×δ （mm） d0-管子外径，mm；δ-壁厚，mm。 管内径di=d0-2δ mm 例子：某钢管为Φ108×4mm，求内径。 管内径di=d0-2δ=108-2×4=100mm=0.1m 2．4 流动类型与雷诺准数 雷诺实验装置如图所示：

+()22(3)层(滞)流：有条不紊，相互无混杂，一条平稳的直线；湍(紊)流：杂乱无章，相互混杂。如何区分这两种流动状态，由无量纲准数一雷诺数Re来判断。Re = dupu式中：d-管道内径，m;u-流体平均流速，m/s;p为流体密度，kg/m；μ为流体粘度，Pa·S。流型的判别：Re≥4000时，湍流；Re≤2000时，层流。2000<Re<4000时，流型不定，但端流的可

层(滞)流：有条不紊，相互无混杂，一条平 稳的直线； 湍(紊)流：杂乱无章，相互混杂。 如何区分这两种流动状态，由无量纲准数— 雷诺数 Re 来判断。 μ duρ Re = 式中：d-管道内径，m； u-流体平均流速，m/s； ρ为流体密度，kg/m3 ； μ为流体粘度，Pa·s。 流型的判别： Re≥4000 时，湍流； Re≤2000 时，层流。 2000＜Re＜4000 时，流型不定，但湍流的可

能性更大。雷诺数的物理意义：惯性力和粘性力之比。2.5 流体在管内的流动阻力流体在管路中流动时的阻力可分为直管阻力和局部阻力两种。流体从管路的一处流到另一处的总流动阻力（或称总能量损失）ZL,为该两点之间的直管阻力L,与局部阻力L,，之和，即ZL, = L, + L,式中ZL,的单位为J/kg，即每1kg流体的总能量损失。2.5.1直管阻力L,的计算达西给出了层流与流情况下计算直管阻力的通式，称为达西公式，其表达式如下:Ly=aln(1)na2Ap, = pL, = pu或(2)d 2式中：l,d一分别为直管长度和管子内径，m;

能性更大。 雷诺数的物理意义：惯性力和粘性力之比。 2．5 流体在管内的流动阻力 流体在管路中流动时的阻力可分为直管 阻力和局部阻力两种。 流体从管路的一处流到另一处的总流动 阻力（或称总能量损失）∑Lf 为该两点之间 的直管阻力 与局部阻力 Lf 之和，即 ' Lf ' ∑ += LLL fff 式中 的单位为 J/kg，即每 1kg 流体的 总能量损失。 ∑Lf 2.5.1 直管阻力Lf 的计算 达西给出了层流与湍流情况下计算直 管阻力的通式，称为达西公式，其表达式如 下： 2 2 u d l Lf = λ （1） 或 2 2 u d l Lp f f ρ ==Δ λρ （2） 式中： , dl —分别为直管长度和管子内径，m；

u一流体在管中的平均流速，m/s;p一流体的密度，kg/m;Ap,一因流动阻力而引起的压强降，Pa;入一摩擦系数，它是雷诺准数与管壁粗糙度的函数，其值可由图1-17（称为莫迪图）查取。在莫迪图中，右上角虚线以上区域的入仅与△/d有关，而与Re无关，这一区域称为阻力平方区或完全湍流区。在特殊情况下，还可用公式计算：（1）层流情况下（Re≤2000时）1= 64(3)Re（2）光滑管流情况下(Re=3×103～1×105） = 0.3164(4)Re0.25-般玻璃管、铜管和铅管可看作光滑管。若将式（3）代入式（2），整理可得：32μluAp:d?上式称为哈根-泊逻叶（Hagon-Poiseuille）

u—流体在管中的平均流速，m/s； ρ—流体的密度，kg/m3 ； Δp f —因流动阻力而引起的压强降，Pa； λ—摩擦系数，它是雷诺准数与管壁粗 糙度的函数，其值可由图 1-17（称为莫迪图） 查取。 在莫迪图中，右上角虚线以上区域的λ 仅与Δ/ｄ有关，而与 Re 无关，这一区域称 为阻力平方区或完全湍流区。 在特殊情况下，还可用公式计算： （1）层流情况下（Re≤2 000 时） Re 64 λ = （3） （2）光滑管湍流情况下 （ ～ ） 3 ×= 103Re 5 ×101 25.0 Re 3164.0 λ = （4） 一般玻璃管、铜管和铅管可看作光滑管。 若将式（3）代入式（2），整理可得： 2 32 d lu p f μ =Δ 上式称为哈根-泊谡叶（Hagon-Poiseuille）