《测量学》课程教学资源(PPT课件)第六章 测量误差理论

测量误差理论测量误差系统误差:在相同观测条件下,对某一未知量进行一系列的观测,若误差的大小和符号保持不变,或按照一定的规律变化。偶然误差:在相同观测条件下,对某一未知量进行一系列的观测,从单个误差看其大小和符号的出现,没有明显的规律,但从一系列误差总体看,则有一定的统计规律
测量误差理论 测量误差 系统误差:在相同观测条件下,对某一未知量 进行一系列的观测,若误差的大小和符号保持 不变,或按照一定的规律变化。 偶然误差:在相同观测条件下,对某一未知量 进行一系列的观测,从单个误差看其大小和符 号的出现,没有明显的规律,但从一系列误差 总体看,则有一定的统计规律
偶然误差的特性△=L-X·真误差的定义:L:观测值,X:真值误差的区间A为正值△为负值ViVi频率立个数Vi个数V频率inndnAdn21210~0.20.6500.1300.6500.13019190.5850.2~0.40.1170.1170.5851512 0.4650.4~0.60.0930.0740.3709110.0560.2800.0680.3400.6~0.8980.8~1.00.0560.2800.0490.245561.0~1.20.0310.1550.0370.185131.2~1.40.0060.0300.0180.090121.4~1.60.0060.0300.0120.0600000001.6以上80820.4950.505
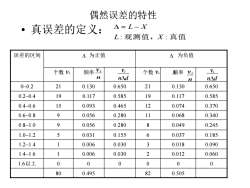
偶然误差的特性 • 真误差的定义: L : 观测值,X :真值 = L − X 误差的区间 为正值 为负值 个数 频率 个数 频率 0~0.2 21 0.130 0.650 21 0.130 0.650 0.2~0.4 19 0.117 0.585 19 0.117 0.585 0.4~0.6 15 0.093 0.465 12 0.074 0.370 0.6~0.8 9 0.056 0.280 11 0.068 0.340 0.8~1.0 9 0.056 0.280 8 0.049 0.245 1.0~1.2 5 0.031 0.155 6 0.037 0.185 1.2~1.4 1 0.006 0.030 3 0.018 0.090 1.4~1.6 1 0.006 0.030 2 0.012 0.060 1.6以上 0 0 0 0 0 0 80 0.495 82 0.505 vi vi n vi n vi n d vi n d vi

偶然误差的特性·在一定的观测条件下,偶然误差的绝对值不会超过一定的限值,即超过一定限值的误差,其出现的概率为零绝对值较小的误差比绝对值较大的误差出现的概率大:绝对值相等的止误差和负误差出现的概率相同:偶然误差的数学期望为零,即E(△) = 0,[] = 0limn>00n
偶然误差的特性 • 在一定的观测条件下,偶然误差的绝对值不会超过一 定的限值,即超过一定限值的误差,其出现的概率为 零 • 绝对值较小的误差比绝对值较大的误差出现的概率大; • 绝对值相等的正误差和负误差出现的概率相同; • 偶然误差的数学期望为零,即 0 [ ] lim ( ) 0, = = → n E n

m-AdS()drV210:V21---01taytorIE93

评定精度的标准m [44]·方差的定义: 2=D(A)=E(△")=limn->00n[]·中误差的定义:=D(A)=E(△)=limn->00n[A]·中误差的估值: m=6=±,n·例:真误差△1△2△3△6△4As-2-1-3甲组+20+5-7-1-4乙组+6+5+2m甲=±2.68″mz=±4.67
评定精度的标准 • 方差的定义: • 中误差的定义: • 中误差的估值: • 例: n D E n [ ] ( ) ( ) lim 2 2 = = = → n D E n [ ] ( ) ( ) lim 2 = = = → n [ ] m ˆ = = 真误差 甲组 +5 +2 -2 -1 0 -3 乙组 +6 -7 -1 -4 +5 +2 1 2 3 4 5 6 4.67 2.68 = = m m 乙 甲

中误差的几何意义·可以证明中误差是正态分布曲线上两个拐点的横坐标值。由f"_2=01e200/2元得?-1=0a故=±
中误差的几何意义 • 可以证明中误差是正态分布曲线上两个 拐点的横坐标值。 = − = = − = − 故 得 由 1 0 ( 1) 0 2 1 ( ) 2 2 2 2 2 2 2 f e
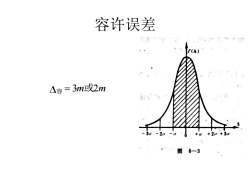
容许误差A△容=3m或2m30+o240客
容许误差 容 = 3m或2m

相对误差将N个关系式平方后再中误差的绝对值1相对误差=T关测值
相对误差 将N个关系式平方后再中 T 1 = = 关测值 误差的绝对值 相对误差

(1)误差传播定律设独立观测值的函数为Z =f(x1,x2.,xn)按台劳级数展开afafafZz+Z=f(x1,x2..Axn)Axix.x2x2Oxnaxafafaf故Z=Axn)Axi+Axx2axnOx将N个关系式平方后再总和得afafa[4Z-]:[△xi]+Ax4x1+x2ax1axaafOAx·Ax1+2Ax·Ax,l+ax,axaxOxafafn-1Ax,lAxaxax
误差传播定律(1) ( . ) ( , ,., ) ( . ) ( , ,., ) 2 2 1 1 2 2 1 1 1 2 1 2 x x x x x x x x x x x x n n n n n n x f x f x f Z x f x f x f Z Z f Z f + + + = + + + + = + = 故 按台劳级数展开 设独立观测值的函数为 . 2 [ ] 2 [ ] 2 [ ] [ ] [ ] [ ] . [ ] 1 1 3 3 1 2 2 2 2 2 2 2 2 1 2 2 1 1 1 1 2 n n n n x x x f x x x f x x x f Z N n n x f x f x f x x f x x f x x f + + + = + + + + − − 将 个关系式平方后再总和得

(2)误差传播定律当N→8时ax1x2oxn两边除以N得当N→时O1mxlmnm0x2axm
误差传播定律(2) m x f m x f m x f m x f m x f m x f x x f x x f x x f Z x x xn Z x x xn n n n n m m N N Z N 2 2 2 2 2 2 1 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 1 2 2 . . [ ] [ ] [ ] . [ ] 1 2 1 2 1 2 = + + + = + + + → = + + + → 或 当 时 两边除以 得 当 时
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《测量学》课程教学资源(PPT课件)第四章 钢尺测距.ppt
- 《测量学》课程教学资源(PPT课件)第五章 直线方向的测量.ppt
- 《测量学》课程教学资源(PPT课件)第八章 地形图测量测绘.ppt
- 《测量学》课程教学资源(PPT课件)第七章 小地区控制测量.ppt
- 《测量学》课程教学资源(PPT课件)第九章 地形图的应用.ppt
- 《测量学》课程教学课件(PPT讲稿)2005年珠峰高程复测.ppt
- 《测量学》课程教学课件(PPT讲稿)1975年首次珠峰高程测量.ppt
- 《测量学》课程教学课件(PPT讲稿)GPS测量的原理与应用.ppt
- 《测量学》课程教学课件(PPT讲稿)GPS测量学综合教案.ppt
- 《测量学》课程教学课件(PPT讲稿)Z-MaxGPS展示.ppt
- 《测量学》课程教学课件(PPT讲稿)徕卡TPS1200全站仪和GPS1200测量系统新产品介绍.ppt
- 《测量学》课程教学课件(PPT讲稿)喜利得激光测量产品介绍.ppt
- 《测量学》课程教学课件(PPT讲稿)国家基本比例尺地形图教案.ppt
- 《测量学》课程教学课件(PPT讲稿)徕卡GPS智能超站仪.ppt
- 《测量学》课程教学资源(试卷习题)合肥工业大学测量学试卷A(题目).doc
- 《测量学》课程教学资源(试卷习题)合肥工业大学测量学B(答案).doc
- 《测量学》课程教学资源(试卷习题)合肥工业大学测量学试卷A(答案).doc
- 《测量学》课程教学资源(试卷习题)合肥工业大学测量学B(题目).doc
- 《测量学》课程实验实习指导书.doc
- 《测量学》课程授课教案(石河子大学电子教案讲义,共十六章).doc
- 《测量学》课程教学资源(PPT课件)第二章 高程测量.ppt
- 《测量学》课程教学资源(PPT课件)第一章 绪论.ppt
- 《测量学》课程教学资源(PPT课件)第三章 角度测量.ppt
- 《机械制造基础》课程教学资源(授课教案)一、工程材料教案.doc
- 《机械制造基础》课程教学资源(授课教案)二、热加工教案.doc
- 《机械制造基础》课程教学资源(授课教案)三、冷加工教案.doc
- 《机械制造基础》课程教学资源(授课教案)四、公差教案.doc
- 《机械制造基础》课程教学资源(授课教案)机制基础(上)教案.doc
- 《机械制造基础》课程教学资源(授课教案)机制基础(下)教案.doc
- 《机械制造基础》课程教学资源(授课教案,石河子大学:胡蓉).doc
- 《机械制造基础》课程教学资源(试卷习题)材料成型综合习题(试题).doc
- 《机械制造基础》课程教学资源(试卷习题)材料成型综合习题(答案).doc
- 《机械制造基础》课程教学资源(试卷习题)机械加工习题(试题).doc
- 《机械制造基础》课程教学资源(试卷习题)机械加工习题(答案).doc
- 《机械制造基础》课程教学课件(PPT讲稿)机械加工工艺概论.ppt
- 《机械制造基础》课程教学课件(PPT讲稿)工程材料的性能.ppt
- 《机械制造基础》课程教学课件(PPT讲稿)纳米科技.ppt
- 《机械制造基础》课程教学课件(PPT讲稿)神奇的纳米材料.ppt
- 《机械制造基础》课程教学课件(PPT讲稿)纳米技术.ppt
- 《机械制造基础》课程教学课件(PPT讲稿)金属的塑性变形.ppt
