同济大学:《理论力学》课程教学课件(PPT讲稿)第五章 分析力学 5.7 哈密顿原理

第五章 分析力学
第五章 分析力学

§5.7哈密顿原理 导读 ·泛函,变分的概念 ·欧拉方程泛函导数 ·哈密顿原理
导读 • 泛函,变分的概念 • 欧拉方程 泛函导数 • 哈密顿原理 §5.7 哈密顿原理

1变分法初步 (1)泛函 质点沿着光滑轨道y=Jyc)从A自由下滑 到B所需时间 J 显然轨道不同J也不同.一般地说,一个 变量J,其值取决于函数=Jyx),就叫做 函数yc)泛函,记做J几yc)】·
1 变分法初步 质点沿着光滑轨道y=y(x)从A自由下滑 到B所需时间 x gy s y J t B A d 2 1 ' v d d 2 + = = = x y A B y=y(x) 显然轨道不同J也不同. 一般地说,一个 变量J, 其值取决于函数y=y(x), 就叫做 函数y(x)泛函,记做 J[y(x) ] . (1) 泛函

(2)变分 选取光滑轨道y=yc),使质点从A自由下 y 滑到B所需时间最短,即求泛函的极值, 就称为变分. 先研究较简单的情况.泛函J只依赖于单个自变量 x,单个函数yx)及其导数y,即 -jFxyy
(2) 变分 x y A B 选取光滑轨道 y=y(x) y=y(x),使质点从A自由下 滑到B所需时间最短, 即求泛函的极值, 就称为变分. 先研究较简单的情况. 泛函J只依赖于单个自变量 x, 单个函数y(x)及其导数y’, 即 J y x F x y y x b a ( ) ( , , ')d =

设想函数关系yx)稍有变动,从y变为y+6,这里⑧y称 为函数yx)的变分.泛函的值也随之而变,其增量 y+ov]-]=[[F(x.y+ov.y+o)-F(x.y.y) 影+小 上式右边叫泛函的变分,记做δJy以. a-g+器
设想函数关系y(x) 稍有变动, 从y变为y+y, 这里y称 为函数y(x)的变分. 泛函的值也随之而变, 其增量 + + − = + + − b a b a y x y F y y F J y y J y F x y y y y F x y y x ' d ' ( , , ' ') ( , , ') d 上式右边叫泛函的变分, 记做J[y]. + = b a y x y F y y F J y ' d '

泛函的极值条件是变分δJy=0
泛函的极值条件是变分J[y]=0. ' d 0 ' = + = b a y x y F y y F J y ( ) − = = b a b a b a b a y x y F x y y F x x y y F y x y F d d ' d ' d d d ' 'd ' = − + b a b a y x y F y x F y y F d 0 d ' d '

一般来说,两端点总是不变的,变分等于零, 0 可ydx=0 dx 这就是泛函取极值的必要条件,叫做这个变分问题 的欧拉方程
一般来说, 两端点总是不变的,变分等于零, = − b a y x y F y x F d 0 d ' d 这就是泛函取极值的必要条件, 叫做这个变分问题 的欧拉方程
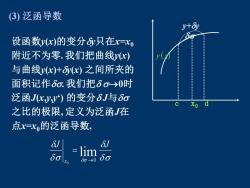
(3)泛函导数 y+Ev 设函数yc)的变分只在x=xo 附近不为零.我们把曲线x) 与曲线yc)+)之间所夹的 面积记作6c.我们把δσ→0时 泛函Jcyy的变分6J与6a 之比的极限,定义为泛函在 点x=x的泛函导数, &J
(3) 泛函导数 设函数y(x)的变分y只在x=x0 附近不为零. 我们把曲线y(x) 与曲线y(x)+y(x) 之间所夹的 面积记作. 我们把 →0时 泛函J(x,y,y‘) 的变分 J与 之比的极限, 定义为泛函J在 点x=x0的泛函导数, J J x lim 0 0 → = y+y y(x) c x0 d

显然 -i 00->0 器 回g of 这样,欧拉方程也可说是泛函J在任一点的泛函导数 等于零 思考:比较欧拉方程和保守力系的拉格朗日方程
显然 0 0 0 d ' d d 1 d ' d d d ' 1 d lim lim 0 0 x d x c d x c y F y x F y x y F y x F y x y F y x J F − = − = − = → → 这样, 欧拉方程也可说是泛函J在任一点的泛函导数 等于零. 思考: 比较欧拉方程和保守力系的拉格朗日方程

(④)变分运算法则 (a)6(A+B)=6A+B (b)δ(AB)=B6A+A6B B6A-A6B B2 (d) 5(dq)=d(ga) 但是 ddga)dq.δd d(ga)dqd(d) dt dt dt2 =0,变分和求导可以互换(等时变分),不然不行 (全变分):
(4) 变分运算法则 (a ) ( A + B) = A + B (b) ( A B) = BA + AB 2 (c) ( ) B B A A B B A − = (d) (d ) d( ) q = q 但是 ( ) ( ) ( ) ( ) 2 2 d d d d d d d d d d d d t q t t q t q t t q t q = − = − t=0, 变分和求导可以互换(等时变分), 不然不行 (全变分)
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第五章 分析力学 5.6 泊松括号与泊松定理.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第五章 分析力学 5.5 哈密顿正则方程.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第五章 分析力学 5.4 小振动.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第五章 分析力学 5.3 拉格朗日方程.ppt
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学课件(讲稿)第五章 分析力学.pdf
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第五章 分析力学 5.1 约束与广义坐标.ppt
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学课件(讲稿)第三章 刚体力学 3.8 刚体的定点转动.pdf
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学课件(讲稿)第三章 刚体力学 3.7 刚体的平面平行运动.pdf
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学课件(讲稿)第三章 刚体力学 3.6 刚体的平动与定轴转动.pdf
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学课件(讲稿)第三章 刚体力学 3.6 刚体的平动与绕固定轴的转动.pdf
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第三章 刚体力学 §3.7 刚体的平面平行运动.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第三章 刚体力学 §3.6 刚体的平动与绕固定轴的转动.ppt
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学课件(讲稿)第三章 刚体力学 3.5 刚体的转动惯量.pdf
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学课件(讲稿)第三章 刚体力学 3.4 刚体的运动方程与平衡.pdf
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学课件(讲稿)第三章 刚体力学(I)刚体介绍,角速度矢量.pdf
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学课件(讲稿)第三章 刚体力学.pdf
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第三章 刚体力学 §3.1 刚体运动的分析 §3.2 角速度矢量 §3.3 欧拉角.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第二章 质点组力学 §2.8 维里定理.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第二章 质点组力学 §2.7 变质量物体的运动.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第二章 质点组力学 §2.5 两体问题 §2.6 质心坐标系与实验室坐标系.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第五章 分析力学 5.8 正则变换.ppt
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学资源(试卷习题)理论力学试卷与参考答案1.pdf
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学资源(试卷习题)理论力学试题及答案2.doc
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学资源(试卷习题)理论力学复习题及参考答案.doc
- 中国石油大学(华东):《理论力学 Theoretical Mechanics》课程教学课件(讲稿)第一章 质点力学——有心力.pdf
- 同济大学:《理论力学》课程教学课件(PPT讲稿)动力学题目讲解(6道).ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)质点及质点组力学复习和习题课.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第三章 刚体力学 §3.8 刚体绕固定点的转动 §3.9 重刚体绕固定点转动的解.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第五章 分析力学 5.2 虚功原理.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第三章 刚体力学 §3.4 刚体运动方程与平衡方程 §3.5 刚体转动惯量.ppt
- 同济大学:《理论力学》课程教学课件(PPT讲稿)第一章 质点力学 §1.9 有心力.ppt
- 海南大学:《材料力学》课程教学课件(PPT讲稿)第一章 绪论(主讲:刘鸿文).ppt
- 海南大学:《材料力学》课程教学课件(PPT讲稿)第二章 轴向拉伸和压缩Axial Tension and Compression.ppt
- 海南大学:《材料力学》课程教学课件(PPT讲稿)第十三章 能量法.pptx
- 海南大学:《材料力学》课程教学课件(PPT讲稿)第十四章 超静定结构.pptx
- 海南大学:《材料力学》课程教学课件(PPT讲稿)第三章 扭转.pptx
- 海南大学:《材料力学》课程教学课件(PPT讲稿)第四章 弯曲内力.pptx
- 海南大学:《材料力学》课程教学课件(PPT讲稿)第七章 弯曲变形(主讲:王涛).pptx
- 海南大学:《材料力学》课程教学课件(PPT讲稿)第八章 组合变形.ppt
- 海南大学:《材料力学》课程教学课件(PPT讲稿)第九章 压杆稳定.ppt
