《畜牧生物统计与实验设计》课程教学课件（PPT讲稿）第七章 方差分析II－双向分类资料（1/3）

上次课内容回顾一、方差分析：2个以上平均数t检验：2个平均数二、单项分类资料：（样本含量相等、不相等）双项分类资料：交叉分组、（有重复、无重复）系统分组（次级样本含量相等，不相等）三、单因子方差分析模型Xij =μ+a; +ej

1 上次课内容回顾 一、方差分析：2个以上平均数 t检验：2个平均数 二、单项分类资料：（样本含量相等、不相等） 双项分类资料： 交叉分组（有重复、无重复） 系统分组（次级样本含量相等、 不相等） 三、单因子方差分析模型 ij i ij X =  + a + e

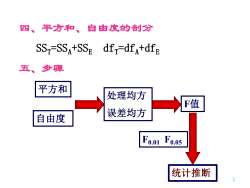
四、平方和、自由度的剖分SSr=SSA+SSedfr=dfa+dfe五、步骤平方和处理均方F值误差均方自由度Fo.01 Fo.05统计推断

2 四、平方和、自由度的剖分 SST=SSA+SSE dfT=dfA+dfE 五、步骤 平方和 自由度 处理均方 误差均方 F值 统计推断 F0.01 F0.05

第7章方差分析-II7.1双向交叉分组一无重复资料双因子方差分析：：试验指标同时受两个因素作用分为交叉分组资料和系统分组资料两类。无重复观察值的交分组资料A因子: Aj, i-l、2......pB因子：B，j-1、2......q因子A的每个水平与因子B的每个水平都彼此交又，产生组合；在每个水平组合只有一个观测值（无重复），共有pq个观测值

3 双因子方差分析：试验指标同时受两个因素作用， 分为交叉分组资料和系统分组资料两类。 第7章 方差分析-Ⅱ 无重复观察值的交叉分组资料 A因子：Ai，i=1、2.p B因子：Bj，j=1、2.q 因子A的每个水平与因子B的每个水平都彼此交叉，产生 组合；在每个水平组合只有一个观测值（无重复），共有pq 个观测值。 7.1 双向交叉分组-无重复资料

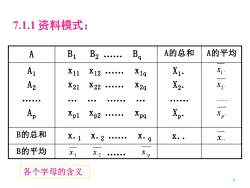
7.1.1资料模式：A的总和A的平均AB1B9B2.A1X1邓一X11X1qX12X2A2X21X2gX22.x,Xp.AXp1XpaXp2B的总和X.qX. 1X.X.2x..B的平均X.1X.qX.29ee各个字母的含义

4 7.1.1 资料模式： A B1 B2 . Bq A的总和 A的平均 A1 A2 . Ap x11 x12 . x1q x21 x22 . x2q . . . . xp1 xp2 . xpq X1. X2. . Xp. B的总和 x.1 x.2 . x.q x. B的平均 . . . . . 2 1 p x x x 1 x. 2 x. q x. x. 各个字母的含义

7.1.2资料模式：Xi, =μ+α, +β, +eji=1,2,..... p;j=1,.. q;X：因子A的第i个水平和因子B的第i个水平组合中的观察值；u：总平均；α：因子A的第i个水平的效应；Zα,=0：因子B的第i个水平的效应；Zβ，=0B:随机误差，假设ei～N（O，α2），且彼此独立。ei:

5 7.1.2 资料模式： ：随机误差，假设 ～ （ ， ），且彼此独立。 ：因子 的第 个水平的效应； ：因子 的第 个水平的效应； ：总平均； ：因子 的第 个水平和因子 的第 个水平组合中的观察值； ， ， ； ， ， ； 2 0 0 0 1 2 . 1 2 .       e e N B j A i X A i B j j q i p i j i j j j i i i j   = = = = i j i j i j x =  + +  + e

7.1.3平方和与自由度的剖分：总平方和为：SS,=(k,-x)i-11(1）先将离均差平方和改写为：(X, - X)? =[(Xi. - X)+(X j - X)+(X, - X,. - X, +X)=(Xi. -X)? +(X, -X)? +(X, -X,.-X, +X)2 +乘积项(2)再将两边求和：=0EZ(X, -X)? =ZE(X. -X)* +ZZ(X, -X) +EZ(X, -X,. -X, +X)* =Z(X -Xx)+p(X, -x)* +ZZ(X, -X,.-X, +X)

6 ( ) 2 1 1 = = − n i k j T i j 总平方和为：SS ＝ x x 7.1.3 平方和与自由度的剖分： = − + − + − − + + 乘积项 − = − + − + − − + 2 . 2 . 2 . 2 . . . 2 ( ) ( ) ( . ) ( ) [( ) ( ) ( . )] X X X X X X X X X X X X X X X X X X j i j i j i i j i j i j i j （1）先将离均差平方和改写为： （2）再将两边求和： 2 . 2 . 2 . 2 . 2 . 2 . 2 ( ) ( ) ( . ) ( ) ( ) ( . ) ( )        − + − + − − + − + − + − − + = − = q X X p X X X X X X X X X X X X X X X X i j i j i j i j i j i j i j i j ＝0

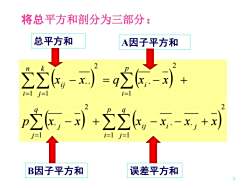
将总平方和部分为三部分：总平方和A因子平方和kn) =q(,-x)MM(xj - x..)十i=1i-l j=12p(s,-) +)2(, -x. -x,+x)j=1i=l j=l←←误差平方和B因子平方和

7 ( ) ( ) ( ) ( ) 2 1 1 2 1 2 1 2 1 1 . . . . .     = = = = = = − + − − + − = − + p i q j i j i j q j j p i i n i k j i j p x x x x x x x x q x x 总平方和 A因子平方和 B因子平方和 误差平方和 将总平方和剖分为三部分：

A因子平方和：A因子各水平的平均数q之(-) =SSa与总平均数的离差平方和。反映了A因子各水平的效应的差异。i=lB因子平方和：B因子各水平的平均数P(,-)=SS,与总平均数的离差平方和。反映了B因子各水平的效应的差异。j=1误差平方和：剔除了A因子和B之之(b, -x, -x, +x)=SSE因子的影响后的影响因素。i=l ,j=l

8 ( ) A p i q xi − x = SS = 2 1 . ( ) B q j p x j − x = SS = 2 1 . ( ) E p i q j  xi j − xi − x j + x = SS = = 2 1 1 . . A因子平方和: A 因子各水平的平均数 与总平均数的离差平方和。反映了A因 子各水平的效应的差异。 误差平方和: 剔除了A因子和B 因子的影响后的影响因素。 B因子平方和: B 因子各水平的平均数 与总平均数的离差平方和。反映了B因 子各水平的效应的差异

总平方和=A因子平方和+B因子平方和+误差平方和SST =SSA+SSSB+SSF

9 总平方和 =A因子平方和+B因子平方和+误差平方和 SST = SSA + SSB + SSE

平方和的计算公式(X..)21.矫正项CT:pq2.总平方和SS =Z(X, -X.) - ZZX,? -CTSS =(x.-x) _ ExCT3.A因子平方和q10

10 平方和的计算公式: SST =(Xi j − X ) =Xi j −CT 2 2 . ( ) C T q X SS q X X i A =  i − =  − 2 2 . . . 2.总平方和 3.A因子平方和 1. 矫正项 pq X CT 2 ( .) =