《畜牧生物统计与实验设计》课程授课教案（PPT讲稿）第十二章 协方差分析 Analysis of covariance（ANCOVA）

第十二章协方差分析Analysis of covariance(ANCOVA)概述协方差分析的模型与假定单向分类资料的协方差分析双向分类资料的协方差分析

第十二章 协方差分析 Analysis of covariance (ANCOVA) ⚫概述 ⚫协方差分析的模型与假定 ⚫单向分类资料的协方差分析 ⚫双向分类资料的协方差分析

NAES概述概念：将方差分析和回归分析结合起来的一种统计分析方法对变量Y>方差分析：一个或几个因子（分类变量）（连续变量）的影响>回归分析：一个或几个变量对变量Y（连续变量）（连续变量）的影响当试验指标（Y）的变异既受一个或几个分类变量，也受一个或几个连续变量的影响，可采用协方差分析

2 概述 ⚫概念：将方差分析和回归分析结合起来的 一种统计分析方法 当试验指标（Y）的变异既受一个或几个分 类变量，也受一个或几个连续变量的影响，可 采用协方差分析 ➢方差分析：一个或几个因子（分类变量）对变量Y （连续变量）的影响 ➢回归分析：一个或几个变量（连续变量）对变量Y （连续变量）的影响

OS概述目的>消除连续变量对Y的影响，使方差分析的检验功效更高，结果更可靠·连续变量可能会增大Y的组间差异，导致错误结论·连续变量可能会增大Y的组内变异，降低检验功效>消除分类变量的影响，使回归分析的结果更可靠4

3 概述 ⚫目的 ➢消除连续变量对Y的影响，使方差分析的检 验功效更高，结果更可靠 • 连续变量可能会增大 Y 的组间差异，导致 错误结论 • 连续变量可能会增大 Y 的组内变异，降低 检验功效 ➢消除分类变量的影响，使回归分析的结果更 可靠

TS概述例>比较几种配合饲料对猪的增重效果(近)·试验控制：选用初始体重相同的猪进行分组试验一→方差分析当试验控制不能实现？·统计控制：利用增重对初始重的回归关系，对初始重的影响进行校正回归分析十方差分析三协方差分析?试验控制永远是第一位的！

4 概述 ⚫例 ➢比较几种配合饲料对猪的增重效果 • 统计控制：利用增重对初始重的回归关系，对 初始重的影响进行校正 → 回归分析＋方差分析＝协方差分析 当试验控制不能实现？ 试验控制永远是第一位的！ •试验控制：选用初始体重相同（近）的猪进行 分组试验 →方差分析

AAAS协方差分析的模型和假定模型方差分析Yij =μ +ai +ij*回归分析：Yij = μ* +β(Xij -X,) +6ij协方差分析：=μ+a, +β(Xj, -X,)+ej协变量- β(Xii -X,)=μ+a; +eijiCo-variable-a,=μ+β(Xu,-X,)+ei

5 协方差分析的模型和假定 回归分析： * * ( ) Yij Xij Xi ij =  +  − + 协方差分析： ij i ij i ij Y =  + a + (X − X ) + e ⚫模型 协变量 Co-variable 方差分析： Yij ai ij =  + +  ij ij i i ij Y − （X − X ) =  + a + e ij i ij i ij Y − a =  +  (X − X ) + e

8协方差分析的模型和假定假定>协变量是非随机变量，没有度量误差>Y对协变量的回归是线性的，并且各处理内的回归系数是齐性的>随机误差服从正态分布N(O,α2），且互相独立6

6 协方差分析的模型和假定 ⚫假定 ➢协变量是非随机变量，没有度量误差 ➢Y 对协变量的回归是线性的，并且各处理内 的回归系数是齐性的 ➢随机误差服从正态分布 ，且互相 独立

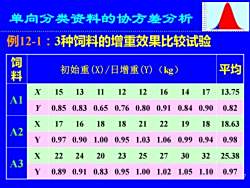
BIES单向分类资料的协方差分析例12-1：3种饲料的增重效果比较试验饲料平均初始重（X）/日增重（Y）(kg)X151311121216141713.75A1Y0.910.820.850.830.650.760.800.840.902219X17161818211818.63A2Y0.980.970.901.000.951.031.060.990.94X222420232527303225.38A3Y0.890.910.830.951.100.971.001.021.05

7 单向分类资料的协方差分析 例12-1：3种饲料的增重效果比较试验 饲 料 初始重(X)/日增重(Y)（kg） 平均 A1 X 15 13 11 12 12 16 14 17 13.75 Y 0.85 0.83 0.65 0.76 0.80 0.91 0.84 0.90 0.82 A2 X 17 16 18 18 21 22 19 18 18.63 Y 0.97 0.90 1.00 0.95 1.03 1.06 0.99 0.94 0.98 A3 X 22 24 20 23 25 27 30 32 25.38 Y 0.89 0.91 0.83 0.95 1.00 1.02 1.05 1.10 0.97

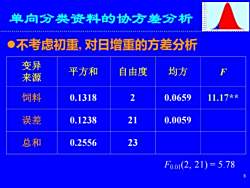
BS单向分类资料的协方差分析●不考虑初重，对日增重的方差分析变异均方平方和自由度F来源饲料211.17**0.13180.0659误差210.12380.0059总和230.2556F0.01(2, 21) = 5.788

8 单向分类资料的协方差分析 ⚫不考虑初重, 对日增重的方差分析 变异 来源 平方和 自由度 均方 F 饲料 0.1318 2 0.0659 11.17** 误差 0.1238 21 0.0059 总和 0.2556 23 F0.01(2, 21) = 5.78

OS单向分类资料的协方差分析协方差分析1.计算有关统计量·日增重(Y)的各项平方和SST(M), SSA(M)，SSE(M)（误差I)·初始重（X）的各项平方和SSE(X)SST(X), SSA(X),·X和Y的各项乘积和SPT(XY), SPA(XY),SPE(XY)

9 单向分类资料的协方差分析 ⚫协方差分析 1. 计算有关统计量 • 日增重（Y）的各项平方和 SST(Y), SSA(Y), SSE(Y)（误差I） • 初始重（X）的各项平方和 SST(X), SSA(X), SSE(X) • X和Y的各项乘积和 SPT(XY), SPA(XY), SPE(XY)

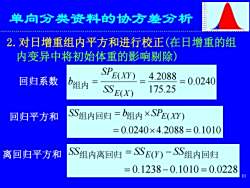
ONIS单向分类资料的协方差分析2.对日增重组内平方和进行校正（在日增重的组内变异中将初始体重的影响剔除SPE(XY)4.2088= 0.0240回归系数b组内SS E(X)175.25SS组内回归=b组内×SPE(XY)回归平方和= 0.0240x 4.2088 = 0.1010SS组内离回归=SSE(Y)－SS组内回归离回归平方和= 0.1238-0.1010= 0.022810

10 单向分类资料的协方差分析 2.对日增重组内平方和进行校正(在日增重的组 内变异中将初始体重的影响剔除) 0.0240 175.25 4.2088 ( ) ( ) = = = E X E XY SS SP 回归系数 b 组内 0.0240 4.2088 0.1010 ( ) =  = 回归平方和 SS组内回归 = b 组内SPE XY 0.1238 0.1010 0.0228 ( ) = − = 离回归平方和 SS组内离回归 = SSE Y − SS组内回归