《畜牧生物统计与实验设计》课程授课教案（PPT讲稿）第9章 简单相关与回归 9.2 简单回归 9.3 简单线性相关与回归的区别和联系

9.2简单回归回归的现象：生物的各性状之间以及性状与环境条件之间都有着一定的相互关系。改变某一性状，就会引起另一性状也发生变异。例如：奶牛的产奶量越高，乳脂率反而减少猪、鸡的生长速度越快，肉质和风味下降。母猪的体重越大，仔猪出生重越大

9.2 简单回归 回归的现象： 生物的各性状之间以及性状与环境条件之间都 有着一定的相互关系。改变某一性状，就会引起另 一性状也发生变异。 例如：奶牛的产奶量越高，乳脂率反而减少。 猪、鸡的生长速度越快，肉质和风味下降。 母猪的体重越大，仔猪出生重越大

回归分析：研究一个变量对另一个变量的单向依存关系，即研究一个变量随另一个变量变化而变化。后一个变量叫自变量，前一个变量叫依变量或应变量

回归分析： 研究一个变量对另一个变量的单向依存 关系，即研究一个变量随另一个变量变化而 变化。后一个变量叫自变量，前一个变量叫 依变量或应变量

一元线性回归的含义要点：(一)研究两个变量之间的回归关系(二）当一个变量数值增大时，另一个变量数值也随着增大或减少。这种增大或减少以坐标的形式来表示，散点图形呈直线的趋势

一元线性回归的含义要点： （一）研究两个变量之间的回归关系。 （二）当一个变量数值增大时，另一个变量 数值也随着增大或减少。这种增大或 减少以坐标的形式来表示，散点图形 呈直线的趋势

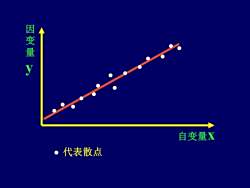
因变量y自变量X 代表散点

自变量x 因 变 量 y 代表散点

回归在统计上表现现象之间的一种最严格的从属关系，是将非确定性变量之间的关系用确定的函数关系表达出来

回归在统计上表现现象之间的一种 最严格的从属关系，是将非确定性变量 之间的关系用确定的函数关系表达出 来

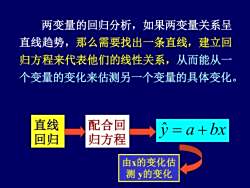
两变量的回归分析，如果两变量关系呈直线趋势，那么需要找出一条直线，建立回归方程来代表他们的线性关系，从而能从一个变量的变化来估测另一个变量的具体变化直线配合回 = a +bx回归归方程由x的变化估测 y的变化

两变量的回归分析，如果两变量关系呈 直线趋势，那么需要找出一条直线，建立回 归方程来代表他们的线性关系，从而能从一 个变量的变化来估测另一个变量的具体变化。 直线 回归 配合回 归方程 y ˆ = a + bx 由x的变化估 测 y的变化

9.2.1一元线性回归的数学模型如果变量X和变量Y之间存在线性函数关系，可用如下方程表示：Y =a+bX(X,, Y,),对于X的每一个取值，Y都有一个确定的值与之对应

9.2.1 一元线性回归的数学模型 如果变量X和变量Y之间存在线性函数关系，可 用如下方程表示： 对于 的每一个取值， 都有一个确定的值与之对应。 ， ， X Y X Y Y a bX i i ( ) = +

在线性回归关系中，对于X的每一个取值，Y的取值是不确定的。但是，我们假定有一个Y的期望值与之对应，或者说Y的期望值与X之间存在线性函数关系：E(Y) = α + βXβ：斜率，称为Y对X的回归系数。截回归参数距含义：当X变化一个单位，可期望Y变化β个单位βyx：下标的第一个为依变量；第二个为自变量Y = E(Y)+e, = α+βX, +ee; ~ N(O,α2)

E(Y) = + X 含义：当 变化一个单位，可期望 变化 个单位。 ：斜率，称为 对 的回归系数。   X Y Y X 在线性回归关系中，对于X的每一个取值，Y的取值是不 确定的。但是，我们假定有一个Y的期望值与之对应，或者 说Y的期望值与X之间存在线性函数关系： 截 距 βYX：下标的第一个为依变量；第二个为自变量 回归参数 ~ (0, ) ( ) 2    e N Y E Y e X e i i = i + i = + i + i

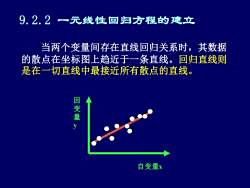
9.2.2 一元线性回归方程的建立当两个变量间存在直线回归关系时，其数据的散点在坐标图上趋近于一条直线。回归直线则是在一切直线中最接近所有散点的直线因变量自变量x

自变量x 因 变 量 y 当两个变量间存在直线回归关系时，其数据 的散点在坐标图上趋近于一条直线。回归直线则 是在一切直线中最接近所有散点的直线。 9.2.2 一元线性回归方程的建立

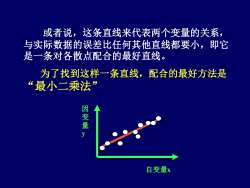
或者说，这条直线来代表两个变量的关系与实际数据的误差比任何其他直线都要小，即它是一条对各散点配合的最好直线为了找到这样一条直线，配合的最好方法是“最小二乘法因变量自变量x

或者说，这条直线来代表两个变量的关系， 与实际数据的误差比任何其他直线都要小，即它 是一条对各散点配合的最好直线。 为了找到这样一条直线，配合的最好方法是 “最小二乘法” 自变量x 因 变 量 y