《电路》课程教学资源（A）课件（内容+例题，图片版）第3章 电阻电路的一般分析

第3章电阻电路的一般分析 本章目录 3.1 电路的图 3.2 KCL和KVL的独立方程数 3.3 支路电流法 3.4 网孔电流法 3.5 回路电流法 3.6 结点电压法

重点： 用观察法，熟练应用支路电流法，回路电流 法，结点电压法的“方程通式”写出支路电流方 程，回路电流方程，结点电压方程，并求解。 Y难点 1.独立回路的确定； 2.正确理解每一种方法的依据： 3.含独立电流源和受控电流源的电路的回路电 流方程的列写； 4.含独立电压源和受控电压源的电路的结点电 压方程的列写。 2

第3章预习要求 自主学习3-1电路的图，并按以下要求完成任务： 1理解相关的基本概念： 结点、支路、拓扑图、有向图、连通图、平面图、 网孔、回路等； 2理解树、树支、连支的概念； 3理解树与基本回路（单连支回路）的关系； 4理解网孔数与独立回路数的关系

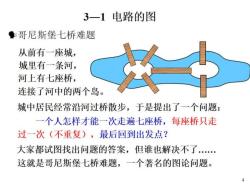
3一1电路的图 ●哥尼斯堡七桥难题 从前有一座城， 城里有一条河， 河上有七座桥， 连接了河中的两个岛。 城中居民经常沿河过桥散步，于是提出了一个问题： 一个人怎样才能一次走遍七座桥，每座桥只走 过一次（不重复），最后回到出发点？ 大家都试图找出问题的答案，但谁也解决不了. 这就是哥尼斯堡七桥难题，一个著名的图论问题。 4

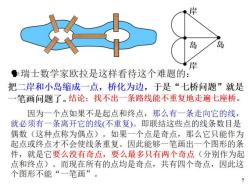
岛 岛 岸 瑞士数学家欧拉是这样看待这个难题的： 把二岸和小岛缩成一点，桥化为边，于是“七桥问题”就是 一笔画问题了。结论：找不出一条路线能不重复地走遍七座桥。 因为一个点如果不是起点和终点，那么有一条走向它的线， 就必须有一条离开它的线（不重复）。即联结这些点的线条数目是 偶数（这种点称为偶点）。如果一个点是奇点，那么它只能作为 起点或终点才不会使线条重复。因此能够一笔画出一个图形的条 件，就是它要么没有奇点，要么最多只有两个奇点（分别作为起 点和终点)。而现在所有的点均是奇点，共有四个奇点，因此这 个图形不能“一笔画

结论：一笔画 1.凡是由偶点组成的连通图，一定可以一笔画成： 画时可以把任一偶点为起点，最后一定能以这个点为终 点画完此图。 2凡是只有两个奇点的连通图（其余都为偶点），一 定可以一笔画成： 画时必须把一个奇点为起点，另一个奇点终点。 3.其他情况的图都不能一笔画出。 (奇点数除以二便可算出此图需几笔画成

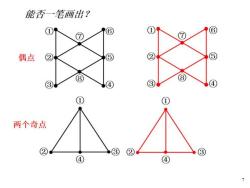
能否一笔画出？ ⑥ 偶点 ② ⑤ ⑧ 8 ③ 3 两个奇点 ③ 2 ④ ④

奥运会的五 环标志能否 一笔画出？ 图论是拓扑学(Topology)的一个分支，是富有趣味和应 用极为广泛的一门学科。图论的概念由瑞士数学家欧拉最 早提出（最早的记载是1736年）。1847年，基尔霍夫首先 用图论来分析电网络，如今在电工领域，图论被用于网络 分析与综合、通讯网络与开关网络的设计、集成电路布局 及故障诊断、计算机结构设计及编译技术等等。 8

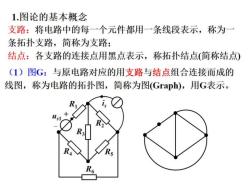
1.图论的基本概念 支路：将电路中的每一个元件都用一条线段表示，称为一 条拓扑支路，简称为支路： 结点：各支路的连接点用黑点表示，称拓扑结点（简称结点） (1)图G:与原电路对应的用支路与结点组合连接而成的 线图，称为电路的拓扑图，简称为图(Grph),用G表示

有时为了需要，可以把元件的串联组合或元件的并 联组合作为一条支路，则这个电路的图如图(c)所示。 3 4 (a) (b) (c) 构成图G的支路是代表一个电路元件或者一些电路元件 的某种组合的一条抽象的线段，可以画成直线或曲线