《医学统计学》课程教学课件（PPT讲稿）第三部份 多元统计分析（logistic）

Logistic回归分析 (Logistic Regression Analysis

Logistic 回归分析 (Logistic Regression Analysis）

Logistic回归分析 多重线性回归分析的前提条件 ·线性；独立；正态；等方差 医学中还常研究二分类因变量（如患病与 未患病、阳性与阴性等)或多分类因变量 与一组自变量(X1,X2,.Xm,)的 关系，线性回归分析方法就无能为力

Logistic 回归分析 多重线性回归分析的前提条件 • 线性；独立；正态；等方差 医学中还常研究二分类因变量（如患病与 未患病、阳性与阴性等）或多分类因变量 与一组自变量（X1，X2，．．．Xm，）的 关系，线性回归分析方法就无能为力

Logistic回归分析 Logistic回归分析可解决： 应变量为： ·二分类； ·无序多分类； ·有序多分类； ·本次教学主要介绍应变量为二分类的 Logistic回归分析

Logistic 回归分析 Logistic 回归分析可解决: 应变量为: • 二分类; • 无序多分类; • 有序多分类; • 本次教学主要介绍应变量为二分类的 Logistic 回归分析

Logistic回归分析 按设计，Logistic回归分析分为： ·成组：非条件Logistic回归分析 ·配对：条件Logistic回归分析

Logistic 回归分析 按设计， Logistic 回归分析分为： • 成组：非条件Logistic 回归分析 • 配对：条件Logistic 回归分析

Logistic回归模型 ·例为探讨超重和肥胖对高血压病的影响， 2004年，某研究者采用整群抽样的方法， 对某地6个镇35周岁以上的常住人口进行高 血压普查，同时收集了身高、体重等相关 信息。整理后资料见下表。 ·目的：建立高血压患病率与体质指数间的 数量关系模型，估计超重与肥胖对高血压 患病的风险

Logistic回归模型 • 例 为探讨超重和肥胖对高血压病的影响， 2004年，某研究者采用整群抽样的方法， 对某地6个镇35周岁以上的常住人口进行高 血压普查，同时收集了身高、体重等相关 信息。整理后资料见下表。 • 目的：建立高血压患病率与体质指数间的 数量关系模型，估计超重与肥胖对高血压 患病的风险

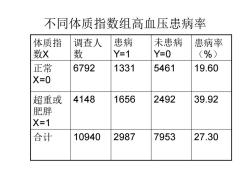
不同体质指数组高血压患病率 体质指 调查人 患病 未患病 患病率 数X 数 Y=1 Y=0 (%) 正常 6792 1331 5461 19.60 X=0 超重或 4148 1656 2492 39.92 肥胖 X=1 合计 10940 2987 7953 27.30

不同体质指数组高血压患病率 体质指 数X 调查人 数 患病 Y=1 未患病 Y=0 患病率 （%） 正常 X=0 6792 1331 5461 19.60 超重或 肥胖 X=1 4148 1656 2492 39.92 合计 10940 2987 7953 27.30

Logistic回归模型 ·因变量为二分类变量，不满足线性回归分析条件， 首先对进行数据变换： g()in)(Onidbs) ·这个变换将取值在0-1间的值转换为值域在 (00,+0∞ 的值。 ·建立log it(π与X的线性模型： .ke对)=R+x或，=+欧

Logistic回归模型 • 因变量为二分类变量，不满足线性回归分析条件， 首先对进行数据变换： • 这个变换将取值在0-1间的值转换为值域在 （ ）的值。 • 建立 与X的线性模型： • 或 ) ln( ) 1 log it( ) ln( = Odds − =     ，+  log it( ) log it() =  0 + X  X   = + − 0 ) 1 ln(

Logistic回归模型 。求解 民+贸 =e(Bo+Bx) 1-π e(B+Br) 1 1+e(B+Bx) 兀= 1+e-(Bo+Bx) ·右端在数学上属于Logistici函数，所以称其为 Logistic回归模型

Logistic回归模型 • 求解 • • 右端在数学上属于Logistic函数，所以称其为 Logistic回归模型 。   X   = + − 0 ) 1 ln( ( ) 0 1 X e     + = − ( ) ( ) 0 0 1 X X e e      + + + = ( ) 0 1 1 X e    − + + =

Logistic回归模型 ·若自变量扩展到个P个，(X1, X2,···XP,),则多个自变量的回归模 型为 log it(π)=B。+BX1+.+B,Xp e(Bo+BX+.+BpXp) Ite(Bo+BiXi++BpXp) 1 I+e-(Bo+BiXi+.+BpXp)

Logistic回归模型 • 若自变量扩展到个P个，（X1， X2，．．．XP，），则多个自变量的回归模 型为 X p X p log it( ) =  0 + 1 1 ++  ( ) ( ) 0 1 1 0 1 1 1 P P P P X X X X e e        + + + + + + + =   ( ) 0 1 1 1 1 X P XP e     − + + + + = 

模型参数的意义 ● B。：常数项（截距），表示模型中所有自变 量均为0时，log it(π)的值； B1,β2、···Bp:回归系数，表示在控 制其他自变量时，自变量变化一个单位所引 起的 log it(π)改变量

模型参数的意义 • Β0 ：常数项（截距），表示模型中所有自变 量均为0时， 的值； • β1 ， β2 、．．． βP：回归系数 ，表示在控 制其他自变量时，自变量变化一个单位所引 起的 改变量。 log it( ) log it( )