《医学统计学》课程教学课件（PPT讲稿）第一部份 基本统计（相关与回归）

线性相关 (linear correlation) 主讲教师 钟晓妮副教授

主讲教师 钟晓妮副教授

线性相关分析： 是在(X,Y)服从正态分布（双变量正态分布）的 假定下，用线性相关的统计分析方法研究两变量间 数量变化关系的密切程度和方向，称为线性相关分 析

线性相关分析： 是在（X，Y）服从正态分布（双变量正态分布）的 假定下，用线性相关的统计分析方法研究两变量间 数量变化关系的密切程度和方向，称为线性相关分 析

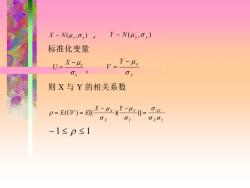
X~N(4,o),Y~N(4,O,) 标准化变量 U=水-4 V= Y-Hy 0x 0y 则X与Y的相关系数 p==承X1于 -1≤p≤1

~ ( , ) X N  x  x ， ~ ( , ) Y N  y  y 标准化变量 x X x U  −  = ， y Y y V  −  = 则 X 与 Y 的相关系数 X Y X Y Y Y X X X Y E UV E         = − − = ( ) = [( )( )] − 1    1

线性相关的性质可由散点图直观的说明，按图中 散点的分布，可归纳为以下几种情况： A 0<p<1 B-1<p<0 Cp=1 Dp=-1 ··. 年0◆◆多·。 Ep=0 Fp=0 Gp=0 Hp=0 线性相关关系示意图

线性相关的性质可由散点图直观的说明，按图中 散点的分布，可归纳为以下几种情况： A 0 < ρ < 1 E ρ = 0 B -1 < ρ < 0 C ρ = 1 D ρ = -1 F ρ = 0 G ρ = 0 H ρ = 0 线性相关关系示意图

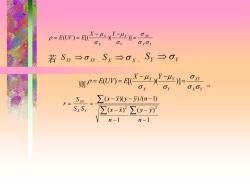
p=EUm=X-LXY-4】=ag OxOY 若Sw→om.Sx→ox.Sy→oy 则P=U=A二4X刀= OX Sm=∑x-x0y-)n-) SxSy ∑x-)2∑0y-列 n-1 n-1

X Y XY Y Y X X X Y E UV E         = − − = ( ) = [ ( )( )] 若 S XY   XY ， X X S   ， SY   Y 则 X Y X Y Y Y X X X Y E UV E         = − − = ( ) = [( )( )]  1 ( ) 1 ( ) ( )( )/( 1) 2 2 − − − − − − − = =    n y y n x x x x y y n S S S r X Y X Y

线性相关分析对样本要求 线性：linear 独立：independent 正态：noma 等方差：equal variance

线性相关分析对样本要求 线性：linear 独立: independent 正态: normal 等方差: equal variance

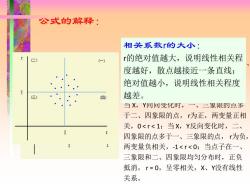
公式的解释： 相关系数r的大小： 的绝对值越大，说明线性相关程 度越好，散点越接近一条直线： 绝对值越小，说明线性相关程度 四) 越差。 当X,Y同同变化时，一、二家限的点多 于二、四象限的点，为正，两变量正相 关，0<r<1;当X,Y反向变化时，二、 四象限的点多于一、三象限的点，为负， 两变量负相关，-1<r<0当点子在一、 三象限和二、四象限均匀分布时，正负 抵消，r=0,呈零相关，X、Y没有线性 关系

公式的解释： r 的符号（方向）： 对于X和Y分别有均数 和 ， 以 和 将坐标系划分为4个象限，在一、 三象限， 取正，二、四象限的点， 取负。 当 X，Y同向变化时，一、三象限的点多 于二、四象限的点，r为正，两变量正相 关，0 < r < 1；当 X，Y反向变化时，二、 四象限的点多于一、三象限的点， r为负， 两变量负相关，-1 < r < 0；当点子在一、 三象限和二、四象限均匀分布时，正负 抵消， r = 0，呈零相关，X、Y没有线性 关系。 X Y X = X Y = Y (X − X )(Y −Y ) (X − X )(Y −Y ) 相关系数r的大小： r的绝对值越大，说明线性相关程 度越好，散点越接近一条直线； 绝对值越小，说明线性相关程度 越差

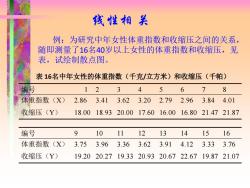
孩性相关 例：为研究中年女性体重指数和收缩压之间的关系， 随即测量了16名40岁以上女性的体重指数和收缩压，见 表，试绘制散点图。 表16名中年女性的体重指数（千克/位方米）和收缩压（千帕） 编号 12 3 4 5 6 7 8 体重指数 (X) 2.863.41 3.623.20 2.792.96 3.844.01 收缩压(Y) 18.0018.9320.0017.6016.0016.8021.4721.87 编号 9 10 11 12 13 14 15 16 体重指数(X) 3.753.963.363.623.914.123.333.76 收缩压(Y) 19.2020.2719.3320.9320.6722.6719.8721.07

线性相 关 例：为研究中年女性体重指数和收缩压之间的关系， 随即测量了16名40岁以上女性的体重指数和收缩压，见 表，试绘制散点图。 编号 1 2 3 4 5 6 7 8 体重指数（X） 2.86 3.41 3.62 3.20 2.79 2.96 3.84 4.01 收缩压（Y） 18.00 18.93 20.00 17.60 16.00 16.80 21.47 21.87 编号 9 10 11 12 13 14 15 16 体重指数（X） 3.75 3.96 3.36 3.62 3.91 4.12 3.33 3.76 收缩压（Y） 19.20 20.27 19.33 20.93 20.67 22.67 19.87 21.07 表 16名中年女性的体重指数（千克/立方米）和收缩压（千帕）

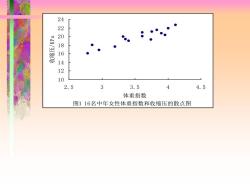
420864 12 10 2.5 3 3.5 4 4.5 体重指数 图116名中年女性体重指数和收缩压的散点图

图1 16名中年女性体重指数和收缩压的散点图 1 0 1 2 1 4 1 6 1 8 2 0 2 2 2 4 2.5 3 3.5 4 4.5 体重指数 收缩压/KPa

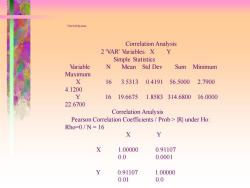
The SASSystem Correlation Analysis 2'VAR'Variables:X Y Simple Statistics Variable N Mean Std Dev Sum Minimum Maximum X 16 3.5313 0.4191 56.5000 2.7900 4.1200 Y 16 19.66751.8583314.6800 16.0000 22.6700 Correlation Analysis Pearson Correlation Coefficients/Prob>R under Ho Rho=0/N=16 X Y X 1.00000 0.91107 0.0 0.0001 0.91107 1.00000 0.01 0.0

The SAS System Correlation Analysis 2 'VAR' Variables: X Y Simple Statistics Variable N Mean Std Dev Sum Minimum Maximum X 16 3.5313 0.4191 56.5000 2.7900 4.1200 Y 16 19.6675 1.8583 314.6800 16.0000 22.6700 Correlation Analysis Pearson Correlation Coefficients / Prob > |R| under Ho: Rho=0 / N = 16 X Y X 1.00000 0.91107 0.0 0.0001 Y 0.91107 1.00000 0.01 0.0