《电路》课程英文课件（PPT讲稿）Chapter 3 Methods of Analysis

Chapter 3Methods of AnalysisSJTU

SJTU 1 Chapter 3 Methods of Analysis

So far, we have analyzed relatively simple circuits byapplying Kirchhoff's laws in combination with Ohm's law.We can use this approach for all circuits, but as theybecome structurally more complicated and involve moreand more elements, this direct method soon becomescumbersome. In this chapter we introduce two powerfultechniques of circuit analysis: Nodal Analysis and MeshAnalysis.These techniques give us two systematic methods ofdescribing circuits with the minimum number ofsimultaneous equations. With them we can analyze almostany circuit by to obtain the required values of current orvoltage.2SJTU

SJTU 2 So far, we have analyzed relatively simple circuits by applying Kirchhoff’s laws in combination with Ohm’s law. We can use this approach for all circuits, but as they become structurally more complicated and involve more and more elements, this direct method soon becomes cumbersome. In this chapter we introduce two powerful techniques of circuit analysis: Nodal Analysis and Mesh Analysis. These techniques give us two systematic methods of describing circuits with the minimum number of simultaneous equations. With them we can analyze almost any circuit by to obtain the required values of current or voltage

Nodal AnalysisStepstoDetermineNodeVoltages1.Select a node as the reference node(ground), define the node voltages1,2,..n- to the remaining n- nodes. The voltages arereferenced with respectto the reference node.2.ApplyKCL to each of the n-1 independentnodes.Use Ohm's law toexpressthebranchcurrents intermsofnodevoltages.3.Solvethe resulting simultaneousequationsto obtaintheunknownnodevoltages3SJTU

SJTU 3 Nodal Analysis • Steps to Determine Node Voltages: 1. Select a node as the reference node(ground), define the node voltages 1 , 2 ,. n-1 to the remaining n-1nodes . The voltages are referenced with respect to the reference node. 2. Apply KCL to each of the n-1 independent nodes. Use Ohm’s law to express the branch currents in terms of node voltages. 3. Solve the resulting simultaneous equations to obtain the unknown node voltages

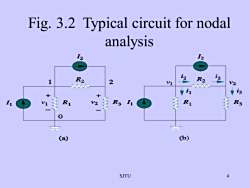
Fig. 3.2 Typical circuit for nodalanalysis15ini2R2R227V1V2订i3R1R3R1I1R3V2V1-0(b)(a)SJTU

SJTU 4 Fig. 3.2 Typical circuit for nodal analysis

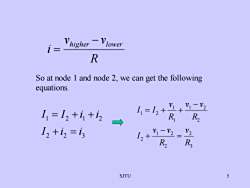
VlowerhigherRSo at node 1 and node 2, we can get the followingequationsV1V.-VI, = I2 +i +izRR2V2I2 +iz =is+V1-V2L.+R2R3SJTU5

SJTU 5 R v v i higher − lower = So at node 1 and node 2, we can get the following equations. 3 2 2 1 2 2 2 1 2 1 1 1 2 R v R v v I R v v R v I I = − + − = + + 2 2 3 1 2 1 2 I i i I I i i + = = + +

In terms of the conductance,equations becomeI, = I2 +GV +G,(Vi- V2)I2 +G2(Vi - V2)=G3V2Can also be cast in matrix form as[G +G22-G2[I-12-G2Gz+G,JLy2↓LI2Some examplesSJTU6

SJTU 6 In terms of the conductance, equations become 2 2 1 2 3 2 1 2 1 1 2 1 2 ( ) ( ) I G v v G v I I G v G v v + − = = + + − Can also be cast in matrix form as       − =            + − − + 2 1 2 2 1 2 3 2 2 1 2 I I I v v G G G G G G Some examples

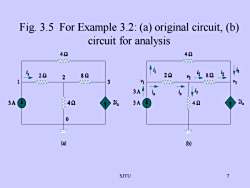
Fig. 3.5 For Example 3.2: (a) original circuit, (b)circuit for analysis4242i22诊2928222822V23V1V33设3AK2iy2ix3A403A400一(a)(b)7SJTU

SJTU 7 Fig. 3.5 For Example 3.2: (a) original circuit, (b) circuit for analysis

Nodal Analysis with Voltage Sources(1)42CaselAAAIf a voltage source is connected1betweenthereferencenodeanda5V1122nonreferencenode, we simply setV2V1V3the voltage at the nonreferencenode equal to the voltage of thei2voltage source.As in the figureright:826210VV =10V8SJTU

SJTU 8 Nodal Analysis with Voltage Sources(1) • Case 1 If a voltage source is connected between the reference node and a nonreference node, we simply set the voltage at the nonreference node equal to the voltage of the voltage source. As in the figure right: v1 =10V

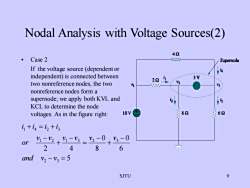
Nodal Analysis with Voltage Sources(2)42Case2WAAASupernodeIf thevoltage source (dependentor4independent)isconnectedbetweeni15V2042twononreferencenodes,thetwoVV2nonreferencenodesformasupernode;we apply bothKVL and25KCL to determine thenode10V89262voltages. As in the figure righti+i=iz+iV2-0V3-0Vi-V2Vi-V3证or十2486andV2- V3 = 5门SJTU9

SJTU 9 Nodal Analysis with Voltage Sources(2) • Case 2 If the voltage source (dependent or independent) is connected between two nonreference nodes, the two nonreference nodes form a supernode; we apply both KVL and KCL to determine the node voltages. As in the figure right: 5 6 0 8 0 2 4 2 3 1 2 1 3 2 3 1 4 2 3 − = − + − = − + − + = + and v v v v v v v v or i i i i

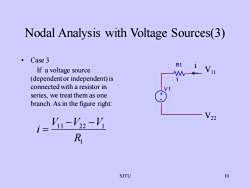
Nodal Analysis with Voltage Sources(3)·Case3R1If avoltage source(dependentorindependent)isconnectedwitharesistorinV1Oseries,wetreatthemas onebranch. As in the figure right22Vi1 - V22 -ViRi10SJTU

SJTU 10 • Case 3 If a voltage source (dependent or independent) is connected with a resistor in series, we treat them as one branch. As in the figure right: Nodal Analysis with Voltage Sources(3) R1 1 V 1 i V11 V22 1 11 22 1 R V V V i − − =