《电路》课程各章习题集（含典型题解）第二章 电阻电路的等效变换

电路习题集第二章电阻电路的等效变换第二章　日电阻电路的等效变换基本要求1.充分理解并掌握等效电路的概念。2.熟练掌握电阻的分压公式和并联电阻的分流公式。3.能熟练运用串联、并联等效电阻的公式对电阻混联电路进行化简。4.会运用电阻的三角形与星形联接相互变换的公式对电路进行化简。5.熟练掌握对含源支路的等效变换。6.能熟练掌握四种受控电源的电压电流关系，初步掌握含有受控电源的简单电路的计算。二、本章要点1.电路的等效变换YR 3IUR4UsURR2RRoRoRi(a)(b)图2—1等效电阻电路两个电路“等效”指他们对外电路的作用效果是相同的，即当电路中某一部分用其等效电路代替后，未被代替部分的电压和电流均应保持不变。如图2一1所示电路中图（b）称为图（a）的等效电路，即：U-U'I=r2.电阻串并联电路R2R11Rs1a-aoa?++ Ui-+U2+UsI1I21IstR2RRiUU(Gr)(G2)Gsbob图2—2电阻串联电路图2-3电阻并联电路1)、电阻串联电路如图2-2所示11

电路习题集 第二章 电阻电路的等效变换 11 第二章 电阻电路的等效变换 一、基本要求 1．充分理解并掌握等效电路的概念。 2．熟练掌握电阻的分压公式和并联电阻的分流公式。 3．能熟练运用串联、并联等效电阻的公式对电阻混联电路进行化简。 4．会运用电阻的三角形与星形联接相互变换的公式对电路进行化简。 5．熟练掌握对含源支路的等效变换。 6．能熟练掌握四种受控电源的电压电流关系，初步掌握含有受控电源的简单电路的计算。 二、本章要点 1.电路的等效变换 图 2—1 等效电阻电路 两个电路“等效”指他们对外电路的作用效果是相同的，即当电路中某一部分用其等 效电路代替后，未被代替部分的电压和电流均应保持不变。如图 2—1 所示电路中图（b） 称为图（a）的等效电路，即： U = U I = I 2. 电阻串并联电路 图 2—2 电阻串联电路 图 2—3 电阻并联电路 ⑴、电阻串联电路如图 2－2 所示

电路习题集第二章电阻电路的等效变换①当n个电阻R、R·Rn串联时：串联等效电阻等于各电阻之和。即:Reg=RI+R2+R3...R-Rk=lRu(k=1、2、m)即：各元件的电压与该元件的电阻值成正比②分压公式为U=Rea式中Reg为串联电路的等效电阻U为第k个电阻Rk上的电压，U为总电压（2）、电阻并联电路如图2一3所示当n个电阻R（或电导G）并联时：①各电阻两端的电压是同一个电压。②并联等效电导等于各电阻元件电导之和。即: G-G++G++G++G-2GE台③分流公式为I-1（1为第k条支路 G中的电流，1为GI总电流）(k1、2、3...)TR, ×R,R=④当两个电阻并联时：等效电阻有R, + R,分流公式可以写成为R,R,1111图2—4两个电阻并联电路R, +R,R, +R,3.如果能判断出电路的某一个支路中没有电流流过，可以把这条支路拿掉，即作为开路，如果能判断出电路中某两点的电位相等,则可以把这两点短路。这在电路的分析、计算中常常是很有用的。4.电阻的星形（Y）和三角形（△）连接的等效变换。(U)Y一△等效变换的公式：Y形电阻=△形相邻电阻的乘积A形电阻之和Y形电阻两两乘积之和A形电阻=-A形不相邻电阻之和=IR.当三个电阻相等时，Ry或Ra=3Ry35.含源支路的等效变换（1）当n个理想电压源串联时其可以用一个等效的理想电压源es来代替，且有12

电路习题集 第二章 电阻电路的等效变换 12 ①当 n 个电阻 R1 、R2.Rn 串联时：串联等效电阻等于各电阻之和。 即： Req=R1+R2+R3.Rn=  = n k 1 Rk ② 分压公式为 U R R U eq k k = (k=1、2、.n) 即：各元件的电压与该元件的电阻值成正比. 式中 Req 为串联电路的等效电阻,Uk为第 k 个电阻 Rk 上的电压，U 为总电压 ⑵、电阻并联电路如图 2－3 所示 当 n 个电阻 R（或电导 G）并联时： ① 各电阻两端的电压是同一个电压。 ② 并联等效电导等于各电阻元件电导之和。 即：G=G1+G2+G3+.+Gn=  = n k 1 Gk ③ 分流公式为 Ik= I G Gk （Ik为第 k 条支路 Gk中的电流，I 为 总电流）(k=1、2、3.n) ④ 当两个电阻并联时：等效电阻有 1 2 1 2 R R R R R +  = 分流公式可以写成为 I R R R I 1 2 2 1 + = ； I R R R I 1 2 1 2 + = 图 2—4 两个电阻并联电路 3．如果能判断出电路的某一个支路中没有电流流过,可以把这条支路拿掉,即作为开路;如果 能判断出电路中某两点的电位相等,则可以把这两点短路。这在电路的分析、计算中常常是 很有用的。 4. 电阻的星形（Y）和三角形（△）连接的等效变换。 (1) Y－△等效变换的公式： 形电阻之和 形相邻电阻的乘积 形电阻   Y = 形不相邻电阻之和 形电阻两两乘积之和 形电阻    = 当三个电阻相等时，  = R 3 1 R 或 R△=3RY 5.含源支路的等效变换 ⑴ 当 n 个理想电压源串联时,其可以用一个等效的理想电压源 es 来代替，且有

电路习题集第二章电阻电路的等效变换ees=esl+es2+nk=l（2）当n个理想电流源并联时其可以用一个等效的理想电流源i.来代替，且有-Zii, =is +is2 +..+isnk=1（3）当若于个实际电压源串联时可以简化成一个等效的电压源，其等效的电压源电压等于各个电压源的电压的代数和，而其等效内阻等于各个电压源的内阻之和，且有1R-RI+R+.+Rn-2Resesi+es2+......+esnk=1=（4）当若干个实际电流源并联时，可以简化成一个等效的电流源，其等效的电流源电流等于各个电流源的电流代数和，而其等效的内电导等于各个电流源的内导之和，且有ZGkG=Gj+G2+...+Gn=i, =isi +is2 +..+isn台（5）当若干个实际电流源串联时，应当先把它们变换成电压源，然后进行简化。（6）当若干个实际电压源并联时，应当先把它们变换成电流源，然后进行简化。(7)理想电压源和理想电流源不能进行等效变换6.受控电源（非独立电源）受控电源是一种非独立电源，其电压和电流与控制它的电压和电流成正比地变化。在分析电路中，对受控原的处理与独立源并无原则区别，唯一要注意的是在对含有受控源的电路进行化简时，必须要注意保留控制量所在的支路。120 Q三、典型例题例2-1试求图2—5所示电路的等效电阻Rab1200a解：从图可见，80Q两端被短接，即电阻值为零。120Q120Q的三个电阻互相并联，然后与60Q的电阻串联，80Q故ab两端的等效电阻为：60Qbo Rs-0+↓×120-1003例2一2试求图2一6所示电路的等效电阻Rab图2—5例2-1 图解：从电路图可见是个平衡电桥，cd两个点电位相等，可视为短路或开路。则202202c当cd短路时：Rab=（20/20）+(60//60)=40Q7a202202当cd开路时：Rab=（20+60）//(20+60)=40260%X60可见：当cd等电位点的时候，将cd点开路或短路处6026026理对电路无任何影响。d图2—6例2-2图13

电路习题集 第二章 电阻电路的等效变换 13 es=es1+es2+.+esn=  = n k sk e 1 ⑵ 当 n 个理想电流源并联时,其可以用一个等效的理想电流源 is来代替，且有  = = + + + = n k s s s sn sk i i i i i 1 1 2  ⑶ 当若干个实际电压源串联时,可以简化成一个等效的电压源,其等效的电压源电压等于各 个电压源的电压的代数和,而其等效内阻等于各个电压源的内阻之和，且有 es=es1+es2+.+esn=  = n k 1 sk e ; R=R1+R2+.+Rn=  = n k Rk 1 ⑷ 当若干个实际电流源并联时，可以简化成一个等效的电流源，其等效的电流源电流等于 各个电流源的电流代数和，而其等效的内电导等于各个电流源的内导之和，且有  = = + + + = n k s s s sn sk i i i i i 1 1 2  ; G=G1+G2+.+Gn=  = n k Gk 1 ⑸ 当若干个实际电流源串联时，应当先把它们变换成电压源，然后进行简化。 ⑹ 当若干个实际电压源并联时，应当先把它们变换成电流源，然后进行简化。 (7)理想电压源和理想电流源不能进行等效变换 6.受控电源（非独立电源） 受控电源是一种非独立电源，其电压和电流与控制它的电压和电流成正比地变化。在 分析电路中，对受控原的处理与独立源并无原则区别，唯一要注意的是在对含有受控源的 电路进行化简时，必须要注意保留控制量所在的支路。 三、典型例题 例2－1 试求图 2—5 所示电路的等效电阻 Rab 解：从图可见，80Ω两端被短接，即电阻值为零。 120Ω的三个电阻互相并联，然后与 60Ω的电阻串联， 故 ab 两端的等效电阻为： Rab=60+ 120 3 1  =100Ω 例 2－2 试求图 2—6 所示电路的等效电阻 Rab 图 2—5 例 2—1 图 解：从电路图可见是个平衡电桥，c,d 两个点电位相等，可视为短路或开路。则 当 cd 短路时: Rab=（20//20）+(60//60)= 40Ω 当 cd 开路时: Rab=（20+60）//(20+60)= 40Ω 可见：当 cd 等电位点的时候,将 cd 点开路或短路处 理对电路无任何影响。 图 2—6 例 2—2 图

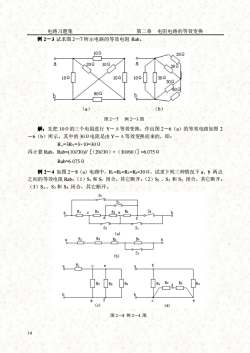
电路习题集第二章电阻电路的等效变换例2-3试求图2—7所示电路的等效电阻Rab。10220206aa~20210270102102102302302O60 .2607(a)(b)图 2—7 例2—3图解：先把10Q的三个电阻进行Y一A等效变换，作出图2一6（a）的等效电路如图2一6（b）所示，其中的30Q电阻是由Y一△等效变换而来的，即：R=3Ry=3×10=30Q再计算Rab：Rab=(10/30)//［（20//30）+（30//60）］=6.075QRab=6.075Q例2一4如图2-8（a）电路中，Ri=R=R3=R4=30Q，试求下列三种情况下a、b两点之间的等效电阻Rab：（1）Si和Ss闭合，其它断开：（2）S2、S3和Ss闭合，其它断开：（3）SL、S3和S4闭合，其它断开。S4S2R1R2R4SsR:ofSsS1(a)R2R4R1Rs0S1(b)fR1a93R上(c)(d)图2-8例2-4图14

电路习题集 第二章 电阻电路的等效变换 14 例 2－3 试求图 2—7 所示电路的等效电阻 Rab。 （a） （b） 图 2—7 例 2—3 图 解：先把 10Ω的三个电阻进行 Y－Δ等效变换，作出图 2－6（a）的等效电路如图 2 －6（b）所示，其中的 30Ω电阻是由 Y－Δ等效变换而来的，即： RΔ=3RY=3×10=30Ω 再计算 Rab：Rab=(10//30)//［（20//30）+（30//60）］=6.075Ω Rab=6.075Ω 例 2－4 如图 2－8（a）电路中，R1=R2=R3=R4=30Ω，试求下列三种情况下 a、b 两点 之间的等效电阻 Rab：（1）S1 和 S5 闭合，其它断开；（2）S2 、S3 和 S5 闭合，其它断开； （3）S1、S3 和 S4 闭合，其它断开。 图 2－8 例 2－4 图

电路习题集第二章电阻电路的等效变换解：根据开关打开和闭合情况，适当改画电路进行分析。（1）根据题意，当Sl、Ss闭合时，电路图可改画成如图2一8（b）所示，可见R4被短接，等效电阻Rab为：Rab=Ri+R2+R3=30+30+30=90Q（2）当S2、S3.、Ss闭合时，电路图可改画成如图2一6（c）所示，这相当于R2.、R、R4三个电阻并联，所以等效电阻Rab为：1Rab=RI+(R2 //R3 // R4) =30+×30=40Q3.（3）当Si、S3.、S4闭合时，电路图可改画成如图2一8（d）所示，此时R2、R3电阻被短接，R和R4并联，等效电阻Rab为：30 ×30 =15 Q2Rab= Ri // R4= 330 + 30例2一5求图2-9所示电路的等效电路。解：等效化简中将与电压源并联的电阻元件拆除，电流源支路中串联的电阻元件置零。如图（b）所示，其余化简如图（c）、（d）、（e）所示25b(a)(b)4V2029hb(c)(d)(e)图2-9例2-5图例2一6求图2-10所示电路的等效电路。解：在图(a)电路中，根据电流源特性3A电流源与6V电压源的串联等效为一个3A的电流源如图(b)所示，然后3A与2A的电流源合并为一个5A的电流源而5A的电流源与8V的电压源的串联等效为一个5A的电流源如图（c)所示。15

电路习题集 第二章 电阻电路的等效变换 15 解： 根据开关打开和闭合情况，适当改画电路进行分析。 （1）根据题意，当S1、S5 闭合时，电路图可改画成如图 2－8（b）所示，可见 R4 被 短接，等效电阻 Rab 为： Rab=R1+R2+R3=30+30+30=90Ω （2）当 S2、S3、S5闭合时，电路图可改画成如图 2－6（c）所示，这相当于 R2、R3、 R4 三个电阻并联，所以等效电阻 Rab 为： Rab=R1+（R2 ∥R3 ∥R4）=30+ 30 3 1  = 40Ω （3）当 S1、S3、S4 闭合时，电路图可改画成如图 2－8（d）所示，此时 R2、R3 电阻 被短接，R1 和 R4 并联，等效电阻 Rab 为： Rab= R1∥R4= 30 30 30 30 +  =15Ω 例 2－5 求图 2－9 所示电路的等效电路。 解： 等效化简中将与电压源并联的电阻元件拆除，电流源支路中串联的电阻元件置 零。如图（b）所示，其余化简如图（c）、（d）、（e）所示 + - 10V 2Ω 6Ω 2A 3Ω - + 4V a b - 2Ω 2A b + 10V - 4V + a 2Ω 2A b - 4V + a 5A 14V 2Ω - b + - + 4V a + 2Ω - b 18V a (a) (b) (c) (d) (e) 图 2－9 例 2－5 图 例 2－6 求图 2－10 所示电路的等效电路。 解:在图(a)电路中,根据电流源特性,3A 电流源与 6V 电压源的串联等效为一个 3A 的电 流源如图(b)所示, 然后 3A 与 2A 的电流源合并为一个 5A 的电流源,而 5A 的电流源与 8V 的电压源的串联等效为一个 5A 的电流源如图(c)所示

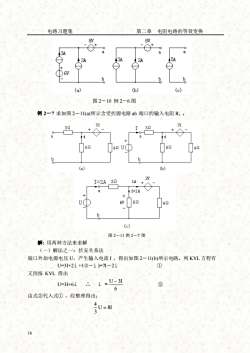
电路习题集第二章电阻电路的等效变换8V8Va3A5A302ADD6V0bb(a)(b)(c)图2-10例2-6图例2一7求如图2-11(a)所示含受控源电路ab端口的输入电阻Ri2i2i3232I+A+Liai1626242UCSbb(a)(b)2V321AI=2Aai=1A+626V451(c)图2-11例2-7图解：用两种方法来求解（一）解法之一：伏安关系法端口外加电源电压U，产生输入电流I，得出如图2一11b)所示电路。列KVL方程有①U=3I+2i +4(1-i )=7I-2i又因按KVL得出.. i _U-31②U=3I+6i6由式②代入式①，经整理得出：4u=81316

电路习题集 第二章 电阻电路的等效变换 16 图 2－10 例 2－6 图 例 2－7 求如图 2－11(a)所示含受控源电路 ab 端口的输入电阻 Ri 。 图 2－11 例 2－7 图 解: 用两种方法来求解 （一）解法之一：伏安关系法 端口外加电源电压 U，产生输入电流 I ，得出如图 2－11(b)所示电路。列 KVL 方程有 U=3I+2i +4(I－i )=7I－2i ① 又因按 KVL 得出 U=3I+6i ∴ i = 6 U − 3I ② 由式②代入式① ，经整理得出： U 8I 3 4 =

电路习题集第二章电阻电路的等效变换U 8x3=62故输入电阻为R=14（二）解法之二：伏安关系推算法设受控电压源控制量i=1A得出如图2一8(c)所示电路，其输入电流按KCL得出为I=1+1=2A端口电压按KVL得出为U=3I+6i=3x2+6x1=12V故端口输入电阻R -U-=601-2例2-8试计算如图2—12所示电路的电源电压Us解：电流参考方向如图2一12所示0.981621I2根据欧姆定律，通过10Q电阻的电流为+I,4.9+12==0.49A1Q10010OUs4. 9V0.491212=0.981==0.5A0.980.98流过1Q电阻的电流为根据LCL得出图2—12例2—8图I=I1+12=Ii=0.5—0.49=0.01A根据KVL,电压源两端的电压为Us=6I+1×Ii=6x0.5+1×0.01=3.01VUs=3.01V17

电路习题集 第二章 电阻电路的等效变换 17 故输入电阻为 Ri = =   = 6 4 8 3 I U （二）解法之二：伏安关系推算法 设受控电压源控制量 i =1A,得出如图 2－8(c)所示电路 ,其输入电流按 KCL 得出为 I=1+1=2A 端口电压按 KVL 得出为 U=3I+6i=3×2＋6×1=12V 故端口输入电阻 Ri = = = 6 2 12 I U 例 2－8 试计算如图 2－12 所示电路的电源电压 US。 解： 电流参考方向如图 2－12 所示 根据欧姆定律，通过 10Ω电阻的电流为 I2 = 0.49A 10 4.9 = I2=0.98I  I= 0.5A 0.98 0.49 0.98 I 2 = = 流过 1Ω电阻的电流为 根据 LCL 得出 图 2－12 例 2－8 图 I=I1＋I2  I1=0.5－0.49=0.01A 根据 KVL,电压源两端的电压为 US=6I＋1×I1=6×0.5＋1×0.01=3.01V US = 3.01V

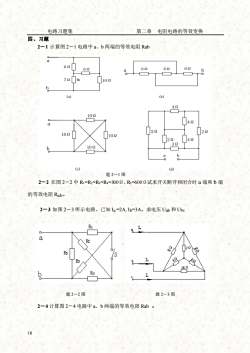
电路习题集第二章电阻电路的等效变换四、习题2一1计算图2一1电路中a、b两端的等效电阻Rab86262626062a0b70R200bo(a)(b)42100o40a2220100109224Q301092b00o(c)(d)题2-1图2-2在图2-2中Ri=R=R=R4=300Q，R=600Q试求开关断开和闭合时a端和b端的等效电阻Rab。2一3如图2一3所示电路，已知Ia=2AIb=3A。求电压Uab和UbcRiLaaRsI16.9R46工题2-2图题2-3图2一4计算图2一4电路中a、b两端的等效电阻Rab18

电路习题集 第二章 电阻电路的等效变换 18 四、习题 2－1 计算图 2－1 电路中 a、b 两端的等效电阻 Rab 题 2－1 图 2－2 在图 2－2 中 R1=R2=R3=R4=300Ω，R5=600Ω试求开关断开和闭合时 a 端和 b 端 的等效电阻 Rab。 2－3 如图 2－3 所示电路，已知 Ia =2A, Ib=3A。求电压 Uab 和 Ubc 题 2－2 图 题 2－3 图 2－4 计算图 2－4 电路中 a、b 两端的等效电阻 Rab 。 10Ω b a (c) 10Ω 10Ω 10Ω (d) 2Ω 3Ω 4Ω a 2Ω b 4Ω 4Ω 2Ω 6Ω a b (a) 7Ω R2 6Ω 6Ω (b) 10Ω a 6Ω b 6Ω

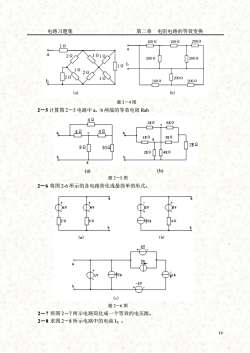
电路习题集第二章电阻电路的等效变换1000200Q100010a20200Q20002000100Q200Q(a)(b)题2-4图2-5计算图25电路中a、b两端的等效电阻Rab422K6KO42423KQ1x9d2K28230.24K2KQ(b)(a)题2-5图2一6将图2-6所示的各电路简化成最简单的形式。od9120O山(a)(b)51(e)题2-6图2一7将图2一7所示电路简化成一个等效的电压源。2-8求图2一8所示电路中的电流Ix19

电路习题集 第二章 电阻电路的等效变换 19 题 2－4 图 2－5 计算图 2－5 电路中 a、b 两端的等效电阻 Rab (a) (b) 题 2－5 图 2－6 将图 2-6 所示的各电路简化成最简单的形式。 题 2－6 图 2－7 将图 2－7 所示电路简化成一个等效的电压源。 2－8 求图 2－8 所示电路中的电流 IX 。 2Ω (a) b 2Ω 1Ω 1Ω a 2Ω 1Ω 1Ω1Ω 200Ω 100Ω 200Ω (b) 200Ω 100Ω 200Ω b 1Ω a 100Ω 200Ω

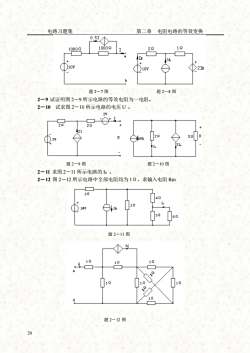
电路习题集第二章电阻电路的等效变换0.5I1210002221000IXJ3A210V21题2-7图题2-8图2一9试证明图2-9所示电路的等效电阻为一电阻2-10试求图2-10所示电路的电压U。2V202020UT题2-9图题2-10图2一11求图2一11所示电路的1o2一12图2—12所示电路中全部电阻均为12，求输入电阻Rin3040129)24V3069题2-11图10101219题2-12图20

电路习题集 第二章 电阻电路的等效变换 20 题 2－7 图 题 2－8 图 2－9 试证明图 2－9 所示电路的等效电阻为一电阻。 2－10 试求图 2－10 所示电路的电压 U 。 题 2－9 图 题 2－10 图 2－11 求图 2－11 所示电路的 I0 。 2－12 图 2－12 所示电路中全部电阻均为 1Ω，求输入电阻 Rin 题 2－11 图 题 2－12 图