石河子大学:《计量经济学》课程PPT教学课件(本科)第三章 多元线性回归模型

石闭手大学 SHIHEZI UNIVERSITY 目录 第一节多元线性回归模型 ■第二节多元线性回归模型的参数估计 ·第三节多元线性回归模型的统计检验 ■第四节多元线性回归模型的预测 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 2 目 录 ◼ 第一节 多元线性回归模型 ◼ 第二节 多元线性回归模型的参数估计 ◼ 第三节 多元线性回归模型的统计检验 ◼ 第四节 多元线性回归模型的预测

名怀手大学 SHIHEZI UNIVERSITY 第一节:多元线性回归模型 一、多元线性回归模型 二、多元线性回归模型的基本假定 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 3 第一节:多元线性回归模型 一、多元线性回归模型 二、多元线性回归模型的基本假定

石所手大学 、多元线性回归模型 SHIHEZI UNIVERSITY ■多元线性回归模型:表现在线性回归模型中的解 释变量有多个。 ■一般表现形式 : Y=B。+B,X+B2X2+.+BX6+4=1,2.,n ■其中:为解释变量的数目,B称为回归参数 regression coefficient ) ■习惯上:把常数项看成为一虚变量的系数,该虚 变量的样本观测值始终取1。 ■此式也被称为总体回归函数的随机表达形式 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 4 ◼多元线性回归模型:表现在线性回归模型中的解 释变量有多个。 ◼一般表现形式: i X i X i k X ki i Y = 0 + 1 1 + 2 2 + + + i=1,2.,n ◼其中:k为解释变量的数目, j称为回归参数 (regression coefficient)。 ◼习惯上:把常数项看成为一虚变量的系数,该虚 变量的样本观测值始终取1。 ◼此式也被称为总体回归函数的随机表达形式 一、多元线性回归模型

名两手大学 多元线性回归模型 SHIHEZI UNIVERSITY ■非随机表达式为: E(Y,|Xi,X2,.X)=B+BX+B2X1+.+BX ■方程表示:各变量X值固定时Y的平均响应。 ■也被称为偏回归系数,表示在其他解释变 量保持不变的情况下,每变化1个单位时 Y的均值E(Y)的变化。 ■或者说P给出了X的单位变化对Y均值的“直 接”或“净”影响。 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 5 ◼非随机表达式为: E Yi X i X i Xki X i X i + k Xki = + + + 1 2 0 1 1 2 2 ( | , , ) ◼方程表示:各变量X值固定时Y的平均响应。 ◼ j也被称为偏回归系数,表示在其他解释变 量保持不变的情况下,Xj每变化1个单位时, Y的均值E(Y)的变化。 ◼或者说j给出了Xj的单位变化对Y均值的“直 接”或“净”影响。 一、多元线性回归模型

石所手大学 、多元线性回归模型 SHIHEZI UNIVERSITY ■总体回归模型n个随机方程的矩阵表达式为 Y X X2 X Ur 1 1l2 XnXnX B Un Y=XB+U 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 6 + = u u u X X X X X X X X X Y Y Y n k kn k k n n n 2 1 2 1 0 2 1 2 2 2 2 1 1 1 2 1 1 2 1 1 1 1 Y = X +U ◼总体回归模型n个随机方程的矩阵表达式为 一、多元线性回归模型
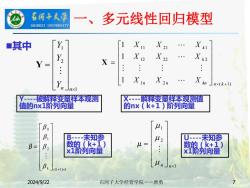
名两子大学 多元线性回归模型 SHIHEZI UNIVERSITY ■其中 1 X21 X k Y 1 X22 Y X .: : Xa」nxk+) nxl Y一被解释变量样本观测 解释变量样本观测值 值的nx1阶列向量 的nx k+1)阶列向量 Bo 41 B B-末知参 U-未知参 B= B2 数的(k+1) u= 数的(k+1) x1阶列向量 .: x1阶列向量 Bx (k+ nxl 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 7 ◼其中 1 2 ( 1) 1 2 2 2 2 1 1 2 1 1 1 1 1 + = n k n n kn k k X X X X X X X X X X ( 1) 1 2 1 0 + = k k β 1 2 1 = n n μ 1 2 1 = n n Y Y Y Y Y-被解释变量样本观测 值的nx1阶列向量 X-解释变量样本观测值 的nx(k+1)阶列向量 B-未知参 数的(k+1) x1阶列向量 U-未知参 数的(k+1) x1阶列向量 一、多元线性回归模型
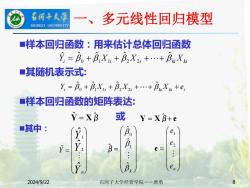
石所手大学 一、多元线性回归模型 SHIHEZI UNIVERSITY ■样本回归函数:用来估计总体回归函数 立=B。+B,Xu+B2X2+.+BaXa ■其随机表示式: Y=B。+BX,+B2X2,+.+BX+e, ■样本回归函数的矩阵表达: Y=XB 或 Y=XB+e ■其中: 月 er B= e= e 2024/9/22 石河子大学经管学院一一唐勇
2024/9/22 石河子大学经管学院--唐勇 8 ◼样本回归函数:用来估计总体回归函数 Yi X i X i ki Xki ˆ ˆ ˆ ˆ ˆ = 0 + 1 1 + 2 2 ++ ◼其随机表示式: i i i ki ki i Y = + X + X + + X + e ˆ ˆ ˆ ˆ 0 1 1 2 2 ◼样本回归函数的矩阵表达: Y ˆ = Xβ ˆ 或 Y = Xβ+ e ˆ ◼其中: = k ˆ ˆ ˆ ˆ 1 0 β = n e e e 2 1 e = Y Y Y n Y ˆ ˆ ˆ 2 1 ˆ 一、多元线性回归模型

二、多元线性回归模型的基本假定 假设1、解释变量是非随机的或固定的,且各X之 间 假设五邂娱有残閨、同方差及不序列 相关性 E(4)=0 Var(4,)=E(4)=o2 Cov(4,4)=E(44)=0 i≠ji,j=1,2,n 假设3,解释变量与随机项不相关 Cov(X)=0 j=1,2.,k 假设4,随机项满足正态分布 4,~N(0,o2) 2024/9/22 石河子大学经管学院一一唐勇 9
2024/9/22 石河子大学经管学院--唐勇 9 ( ) = 0 E i 2 2 Var(i ) = E(i ) = Cov(i , j ) = E(i j ) = 0 i j i, j =1,2, ,n 假设3,解释变量与随机项不相关 Cov(X ji ,i ) = 0 假设4,随机项满足正态分布 ~ (0, ) 2 i N j = 1,2 , k 二、多元线性回归模型的基本假定 假设1、解释变量是非随机的或固定的,且各X之 间 假设2互不相关(无多重共线性) 、随机误差项具有零均值、同方差及不序列 相关性

名所多大学 SHIHEZI UNIVERSITY 第二节、多元线性回归模型的参数估计 一、 普通最小二乘估计 二、 参数估计量的性质 三、样本容量问题 四、估计实例 2024/9/22 石河子大学经管学院一一唐勇 10
2024/9/22 石河子大学经管学院--唐勇 10 一、普通最小二乘估计 二、参数估计量的性质 三、样本容量问题 四、估计实例 第二节、多元线性回归模型的参数估计

名两多大学 普通最小二乘估计 SHIHEZI UNIVERSITY 对于随机抽取的n组观测值(化,X),i=l2,n,j=0,12,.k ■如果样本函数的参数估计值已经得到,则有: 立,=B。+B,X.+B2X2+.+B%Xa i=1,2.n ■根据最小二乘原理,参数估计值应该是下列方程 组的解 Q=0 那。 0-2e-2g-州 那 Q=0 其 ,9 =0 2U-a+月x+月X+.+aX》 那 Q=0 2024/9/22 石河子大学经管学院一一唐勇 11
2024/9/22 石河子大学经管学院--唐勇 11 ◼ 对于随机抽取的n组观测值 Y X i n j k ( i , ji), =1,2, , , = 0,1,2, ◼如果样本函数的参数估计值已经得到,则有: Yi X i X i ki X Ki ˆ ˆ ˆ ˆ ˆ = 0 + 1 1 + 2 2 ++ i=1,2.n ◼根据最小二乘原理,参数估计值应该是下列方程 组的解 = = = = 0 ˆ 0 ˆ 0 ˆ 0 ˆ 2 1 0 Q Q Q Q k 其 中 2 1 1 2 ) ˆ ( = = = = − n i i i n i Q ei Y Y 2 1 0 1 1 2 2 )) ˆ ˆ ˆ ˆ ( ( = = − + + + + n i Yi X i X i k X ki 一、普通最小二乘估计
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 石河子大学:《计量经济学》课程PPT教学课件(本科)第七章 随机解释变量问题.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(本科)第一章 计量经济模型的建立(负责人:唐勇).ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第九章 经典计量经济学应用模型 9.4 计量经济学应用模型变量设定.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第九章 经典计量经济学应用模型 9.3 计量经济学应用模型函数关系设定.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第九章 经典计量经济学应用模型 9.2 计量经济学应用模型总体回归模型设定.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第九章 经典计量经济学应用模型 9.1 计量经济学应用模型类型设定.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第八章 时间序列计量经济学模型 8.3 时间序列的协整和误差修正模型 Cointegration and Error Correction Model.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第八章 时间序列计量经济学模型 8.2 随机时间序列模型 Stochastic Time Serial Model.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第八章 时间序列计量经济学模型 8.1 时间序列的平稳性和单位根检验 Stationary Time Serial and Unit Root Test.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第七章 扩展的单方程计量经济学模型 §7.3 Panel Data模型.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第七章 扩展的单方程计量经济学模型 §7.2 二元选择模型 Binary Choice Model.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第七章 扩展的单方程计量经济学模型 §7.1 选择性样本模型 Selective Samples Model.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第六章 联立方程计量经济模型理论方法 The Theory and Methodology of the Simultaneous-Equations Econometrics Model(SEM,2/2).ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第六章 联立方程计量经济模型理论方法 The Theory and Methodology of the Simultaneous-Equations Econometrics Model(SEM,1/2).ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第五章 经典单方程计量经济学模型(专门问题).ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第四章 经典单方程计量经济学模型(放宽基本假定的模型)§4.3 多重共线性 Multicollinearity §4.4 随机解释变量问题 Random Explanatory Variables.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第四章 经典单方程计量经济学模型(放宽基本假定的模型)§4.1 异方差性 Heteroscedasticity §4.2 序列相关性 Serial Correlation.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第三章 经典单方程计量经济学模型(多元线性回归模型)Multiple Linear Regression Model.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第二章 经典单方程计量经济学模型(一元线性回归模型)The Classical Single Equation Econometric Model - Simple Linear Regression Model.ppt
- 《计量经济学》课程教学资源(PPT课件)课程PPT教学课件(第3版)第一章 绪论.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(本科)第九章 单方程计量经济学应用模型.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(本科)第二章 一元线性回归模型.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(本科)第五章 序列相关性.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(本科)第八章 虚拟变量模型.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(本科)第六章 多重共线性.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(本科)第四章 异方差.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第一章 计量经济学绪论 ECONOMETRICS.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第二章 经典单方程计量经济学模型 The Classical Single Equation Econometric Model(一元线性回归模型 Simple Regression Model).ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第二章 经典单方程计量经济学模型 The Classical Single Equation Econometric Model 2.1 回归分析概述.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第二章 经典单方程计量经济学模型 The Classical Single Equation Econometric Model 2.2 一元线性回归模型的参数估计.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第二章 经典单方程计量经济学模型 The Classical Single Equation Econometric Model 2.3 多元线性回归模型的估计.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第二章 经典单方程计量经济学模型 The Classical Single Equation Econometric Model 2.4 多元线性回归模型的统计检验.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第二章 经典单方程计量经济学模型 The Classical Single Equation Econometric Model 2.5 异方差性.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第二章 经典单方程计量经济学模型 The Classical Single Equation Econometric Model 2.6 序列相关 Serial Correlation.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第二章 经典单方程计量经济学模型 The Classical Single Equation Econometric Model 2.7 多重共线性 Multi Collinearity.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第二章 经典单方程计量经济学模型 The Classical Single Equation Econometric Model 2.8 随机解释变量问题.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第三章 联立方程计量经济模型理论方法 Theory and Methodology of Simultaneous-Equations Econometrics Model 3.1 联立方程计量经济模型的提出 6.2 联立方程计量经济学 3.3 联立方程计量经济学模型的识别(1/2).ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第三章 联立方程计量经济模型理论方法 Theory and Methodology of Simultaneous-Equations Econometrics Model 3.3 联立方程计量经济学模型的识别(2/2).ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第三章 联立方程计量经济模型理论方法 Theory and Methodology of Simultaneous-Equations Econometrics Model 3.3 联立方程模型的单方程估计方法 Single-Equation Estimation Methods.ppt
- 石河子大学:《计量经济学》课程PPT教学课件(硕士生)第三章 联立方程计量经济模型理论方法 Theory and Methodology of Simultaneous-Equations Econometrics Model 3.4 联立方程计量经济学模型的系统估计方法 the Systems Estimation Methods.ppt
