电子科技大学：《DSP算法实现技术与架构 VLSI Digital Signal Processing Systems Design and Implementation》课程教学资源（课件讲稿）Chapter 10 递归滤波器 Pipelined and Parallel Recursive and Adaptive Filters

电子料做女学 University of Electroe Scioncad TechofChina /986 Chapter 10 Pipelined and Parallel Recursive and Adaptive Filters Xiang LING National key Lab of Science and Technology on Communications

Chapter 10 Pipelined and Parallel Recursive and Adaptive Filters Xiang LING National Key Lab of Science and Technology on Communications

S- 10.1 Introduction /96 IIR digital filters are often preferred since a specified spectrum can be implemented using a much lower order IIR filter than FIR. Recursive digital filters cannot be easily pipelined or processed in parallel due to the presence of feed back loops in this filter. ■ Look-ahead computation and incremental block processing techniques are used for pipelined and paralleled recursive digital filters. 2

2 10.1 Introduction  IIR digital filters are often preferred since a specified spectrum can be implemented using a much lower order IIR filter than FIR.  Recursive digital filters cannot be easily pipelined or processed in parallel due to the presence of feed back loops in this filter.  Look-ahead computation and incremental block processing techniques are used for pipelined and paralleled recursive digital filters

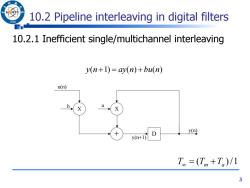
10.2 Pipeline interleaving in digital filters 966 10.2.1 Inefficient single/multichannel interleaving y(n+1)=ay(n)+bu(n) u(n) a X X D y四 y(n+1) T=(Tm+T)/1 3

3 10.2 Pipeline interleaving in digital filters 10.2.1 Inefficient single/multichannel interleaving y(n 1)  ay(n)  bu(n) X + D X y(n) u(n) b a y(n+1) T  (Tm Ta )/1

966 How to decrease 70？ An M-stage pipelined version by inserting (M-1) additional latches. a The clock period can be reduced by M times in principle. But the latency will increase to M clock periods. ■ For the case of a single time series,this array will be useful for only 20%of the time. u(n) 6 a 十 5D @ 4

4  How to decrease T∞ ?  An M-stage pipelined version by inserting (M-1) additional latches.  The clock period can be reduced by M times in principle.  But the latency will increase to M clock periods.  For the case of a single time series, this array will be useful for only 20% of the time. X + 5D X y(n) u(n) b a

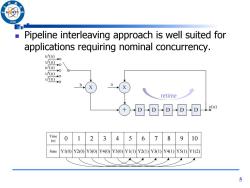
/966 Pipeline interleaving approach is well suited for applications requiring nominal concurrency. u'( u2(n) 0 u(n)o uD)→o u(n)o a retime ①D-D-D-D-D Time 4 (n) 0 1 2 3 5 6 7 8 9 10 State Y1(0)Y2(0) Y3(0)Y40)Y5(0)Y1(1)Y2(1)Y31)Y41)Y5(1)Y1(2) 5

 Pipeline interleaving approach is well suited for applications requiring nominal concurrency. 5 Time (n) State 0 1 2 3 4 5 6 7 8 9 10 Y1(0) Y2(0) Y3(0) Y4(0) Y5(0) Y1(1) Y2(1) Y3(1) Y4(1) Y5(1) Y1(2) retime

/986 10.2.2 Efficient single channel interleaving Problems with M-slow implementation: A sample rate M times slower than the clock rate, Inefficient utilization of processing elements. Look-ahead transformation overcomes these problems,in which the linear recursion is first iterated a few times to create additional concurrency. 2021年2月 6

2021年2月 6 10.2.2 Efficient single channel interleaving  Problems with M-slow implementation:  A sample rate M times slower than the clock rate,  Inefficient utilization of processing elements.  Look-ahead transformation overcomes these problems, in which the linear recursion is first iterated a few times to create additional concurrency

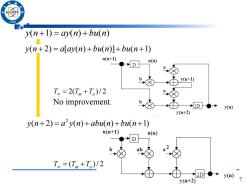
/966 y(n+1)=ay(n)+bu(n) y(n+2)=alay(n)+bu(n)]+bu(n+1) u(m+1) u(n) D y(n+1) T,=2(Tm+Ta)/2 No improvement. 2D●→ y(n+2) y(n+2)=a2y(n)+abu(n)+bu(n+1) u(n+1) u(n) D b ab T=(Tm+T)/2 →2D◆→ y() y(m+2) 7

7 y(n  2)  a[ay(n)  bu(n)] bu(n 1) ( 2) ( ) ( ) ( 1) 2 y n   a y n  abu n  bu n  T  2(Tm Ta )/ 2 T  (Tm Ta )/ 2 No improvement. y(n 1)  ay(n)  bu(n)

/966 Applying (M-1)steps of look-ahead to the iteration.we can obtain an equivalent implementation. M-1 y(n+M)=a“y(n)+∑abu(n+M-1-i) i=0 u(+M-1) u(n+M-2) u(D) D I- ）T。=(Tm+Ta)/M y(n+M) Time (n) 0 2 3 4 5 6 7 8 9 10 State Y(-4) Y(-3) Y(-2) Y(-1) Y(0) Y(1) Y(2) Y(3) Y(4) Y(5) Y(6) 2021年2月 8

2021年2月 8  Applying (M-1) steps of look-ahead to the iteration. we can obtain an equivalent implementation. ( ) ( ) ( 1 ) 1 0 y n M a y n a bu n M i M i M i         T  (Tm Ta )/ M Time (n) State 0 1 2 3 4 5 6 7 8 9 10 Y(-4) Y(-3) Y(-2) Y(-1) Y(0) Y(1) Y(2) Y(3) Y(4) Y(5) Y(6)

/96 M-1 y(n+M=a“y(n)+∑abn+M-1-) i=0 the loop delay is Z-M instead of Z-1,which means that the loop computation must be completed in Mclock cycles (not 1 clock cycle). The iteration bound of this computation is (TM+TA)/M, which corresponds to a sample rate /times higher than that of the original filter. The terms aib,aM can be pre-computed. The second term in the right hand side is the look-ahead computation term (referred to as the /ook-ahead comp/exity);it is non-recursive and can be easily pipelined. 2021年2月 9

2021年2月 9  the loop delay is Z-M instead of Z-1 , which means that the loop computation must be completed in M clock cycles (not 1 clock cycle).  The iteration bound of this computation is (TM+TA )/M, which corresponds to a sample rate M times higher than that of the original filter.  The terms aib, aM can be pre-computed.  The second term in the right hand side is the look-ahead computation term (referred to as the look-ahead complexity); it is non-recursive and can be easily pipelined. ( ) ( ) ( 1 ) 1 0 y n M a y n a bu n M i M i M i        

/96 Look-ahead computation has allowed a single serial computation to be transformed into M independent concurrent computations,and to pipeline the feedback loop to achieve high speed filtering of a single time series while maintaining full hardware utilization. Assume the multiplier and the adder can be conveniently pipelined,the iteration bound can be achieved by retiming or cutset transformation 2021年2月 10

2021年2月 10  Look-ahead computation has allowed a single serial computation to be transformed into M independent concurrent computations, and to pipeline the feedback loop to achieve high speed filtering of a single time series while maintaining full hardware utilization.  Assume the multiplier and the adder can be conveniently pipelined, the iteration bound can be achieved by retiming or cutset transformation